这一部分知识的直观感受: 新的定义巨多无比但是内容却又都很 trivial. 需要对定义相当熟悉.
“根据定义.” ——张运清教授.
1. Parser 介绍
1.1. Parser 的功能
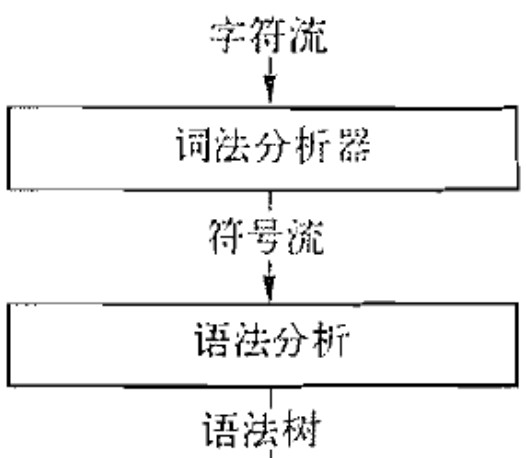
Parser 接受经过 Lexer 解析之后产生的符号流, 生成一个语法树
1.2. Parser 的三种设计方法
难度递增
- Parser Generator (e.g. ANTLR4)
- Handwritten Lexer (由于难度太大而直接跳过)
- Automated Lexer
2. Parser Generator —— ANTLR4
文法 (grammar), 词法 (lexical) 和语法 (syntax) 的区别
这一部分的具体代码可以查看蚂蚁老师的视频
2.1. ANTLR4 消除文法二义性
编程语言的文法不能是二义性的. 下面介绍几种经典的二义性文法.
1. 悬空的ELSE
一个经典的二义性的例子是如下的文法 (悬空的else):
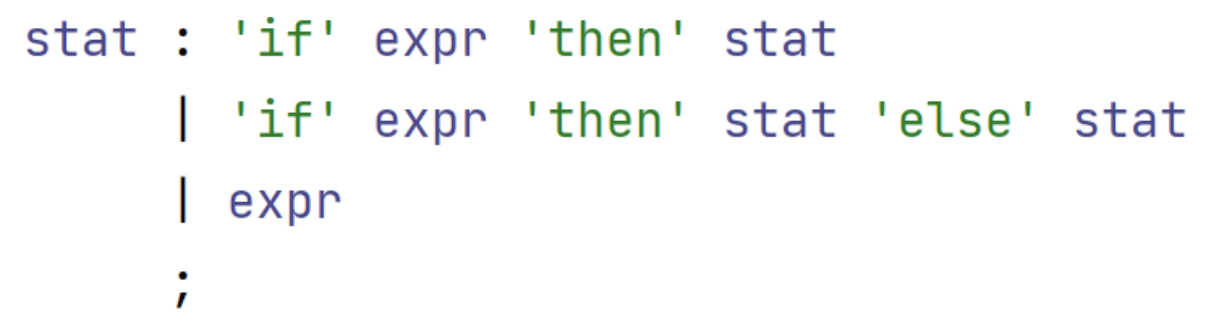
如果给出如下的语句, 显然会产生有歧义的解释:
1 | if a then if b then c else d |
为了消除程序语言解释的二义性, 我们可以将上面的文法改造成没有二义性的写法如下:

但是这样的写法不够好, 因为文法变得非常的复杂.
不过, ANTLR4有自动消除文法二义性的功能, 即: 只需要给出第一种写法, ANTLR4能自动解析出和第二种写法相同的效果. ANTLR4消除二义性的方式是, 对于可能有多种解释方式的语句, 写在前面的解释方式具有更高的优先级, 可以优先被解释.
2. 运算符结合性导致的二义性
结合性,就是当一个表达式中出现多个优先级相同的运算符时,先执行哪个运算符:先执行左边的叫左结合性,先执行右边的叫右结合性.
对于如下的文法:

如果给出如下的简单语句:
1 | 1 - 2 - 3 |
可能会解析成两种结果
- 左结合:
(1 - 2) - 3 - 右结合:
1 - (2 - 3)
同样, ANTLR4也可以消除这样的二义性, 其做法是: 对于没有明确规定是左结合还是右结合的运算符, 默认是左结合. 对于想要明确指出是右结合的运算符, 可以用如下的写法:

3. 运算符优先级导致的二义性

同样, ANTLR4 认为写在前面的运算符具有更高的优先级. 如上的语句不需要进行任何的修改, 就可以被 ANTLR4 无歧义地识别. 但是值得注意的是, 一些 上古时期的 语法分析器生成器并不能正确地处理优先级.
理论上, 我们还是可以把这种写法改成无歧义的写法, 一种方法是写成 左递归(左结合) 的形式:

之所以说这是左递归的写法, 因为运算符左侧递归调用了 expr (而在原本的写法中, 运算符左侧和右侧都递归调用了 expr, 因此既可以用左结合的方法来解释, 也可以用右结合的方法来解释)
另一种改造方法是改造成 右递归(右结合) 的形式 (which is not trivial):

不难发现, 虽然这样也能算出正确的结果, 但是副作用是把减号和乘号变成了右结合运算符
2.2. ANTLR4 如何处理节点事件
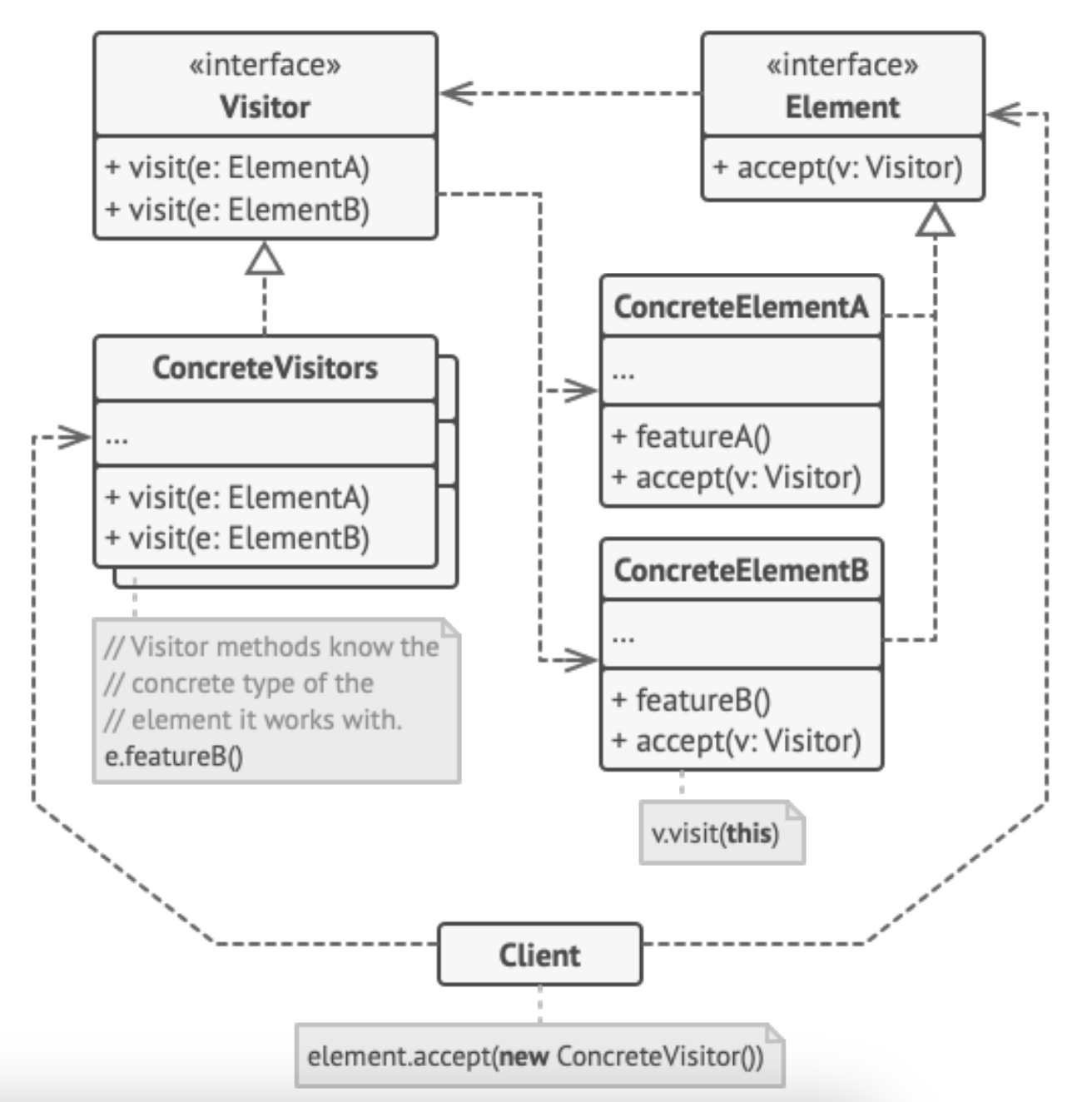
ANTLR4考虑了两种处理节点事件的设计模式: Listener模式 和 Visitor模式. 同时, ANTLR4 将“语法树的构建”和“语法树节点事件的处理”有意地分离开来, 使得程序员处理节点事件的难度和复杂度大大降低.
3. CFG
3.1. CFG 的定义
$def:$ 上下文无关文法 (Context-Free Grammar) $G$ 是一个四元组:
其中:
$(1)$ $T$ 是是终结符号 ($\textbf{Terminal}$) 集合, 对应于词法分析器产生的词法单元.
$(2)$ $N$ 是非终结符号 ($\textbf {Non}\mbox-\textbf{terminal}$) 集合.
$(3)$ $P$ 是产生式 ($\textbf {Production}$) 集合.
$(3.1)$ 头部/左部 ($\textbf {Head}$) $A$: 单个非终结符. (这正是 CFG 区别于 CSG 的地方)
$(3.2)$ 体部/右部 ($\textbf {Body}$) $\alpha$: 终结符与非终结符构成的串, 也可以是空串 $\epsilon$.
$(4)$ $S$ 为开始 ($\textbf {Start}$) 符号。要求 $S \in N$ 且唯一.
这里维基百科说得更清楚
与 CFG 相对的概念是 CSG (Context-Sensitive Grammar, 上下文相关文法). 下图给出了一个上下文相关文法的例子
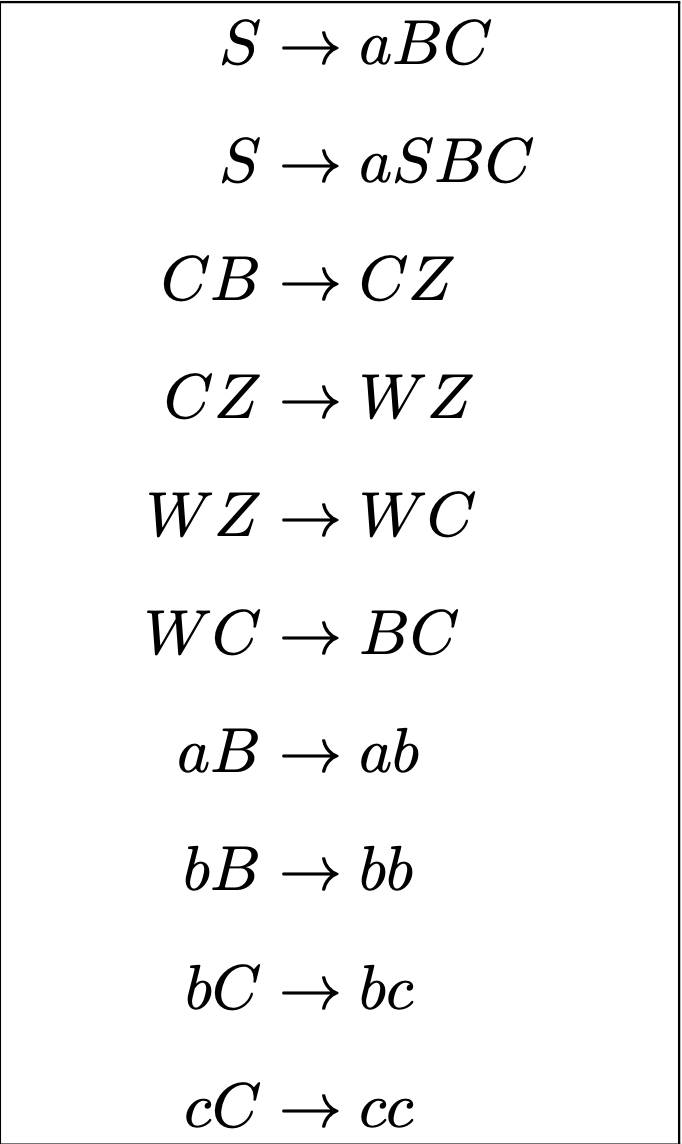
3.2. CFG 的语义
上下文无关文法 $G$ 定义了一个语言 $L(G)$
0. Derivation
推导 (derivation) 指的就是将某个产生式的左边替换成它的右边. 推导时需要考虑两个平凡的问题:
关于推导, 有一些形式化表述:
- $A\Rightarrow \alpha$ : $A$ 经过一步推导得出 $\alpha$
- $A \overset +\Rightarrow \alpha$ : $A$ 经过过一步或多步推导得出 $\alpha$
- $A\overset *{\Rightarrow} \alpha$ : $A$ 经过零步或多步推导得出 $\alpha$
1. Sentential Form
$def: $ 如果 $S \stackrel{*}{\Rightarrow} \alpha$ , 且 $\alpha \in (T\cup N)^*$, $S$ 为开始符号, 则称 $\alpha$ 是文法 $G$ 的一个句型 (Sentential Form)
2. Sentence
$def: $ 如果 $S \overset * \Rightarrow \omega$, 且 $\omega \in T^*$, $S$ 为开始符号, 则称 $\omega$ 是文法 $G$ 的一个句子 (Sentence)
3. Language of Grammar
$def: $ 文法 $G$ 的语言 (Language) $L(G)$ 是它能推导出的所有句子构成的集合
其中 $S$ 为开始符号.
3.3. Chomsky 谱系
语言学家Chomsky在这篇论文中提出了Chomsky谱系, 刻画了不同文法的表达能力.
为什么不使用 强大又优雅 的正则表达式来描述程序设计语言的语法: 可以证明, 正则表达式的表达能力严格弱于上下文无关文法 (实际上这很符合直观感受)
- 每个正则表达式 $r$ 对应的语言 $L(r)$ 都可以使用上下文无关文法来描述
- 存在某种语言, 能用上下文无关文法描述, 但是不能用正则表达式描述 (详见下面的Pumping Lemma)
实际上, Chomsky将文法分成四类, 这四种文法的形式化定义都和上面的CFG类似, 唯一不同的地方就是产生式的规则. 四者的产生式规则区别如下:
| 文法 | 语言 | 自动机 | 产生式规则 |
|---|---|---|---|
| 0-型 | 递归可枚举语言 | 图灵机 | $α \to β$(无限制) |
| 1-型 | 上下文相关语言 | 线性有界非确定图灵机 | $αAβ \to αγβ$ |
| 2-型 | 上下文无关语言 | 非确定下推自动机 | $A \to γ$ |
| 3-型 | 正则语言 | 有限状态自动机 | $A \to aB$ $ A \to a$ |
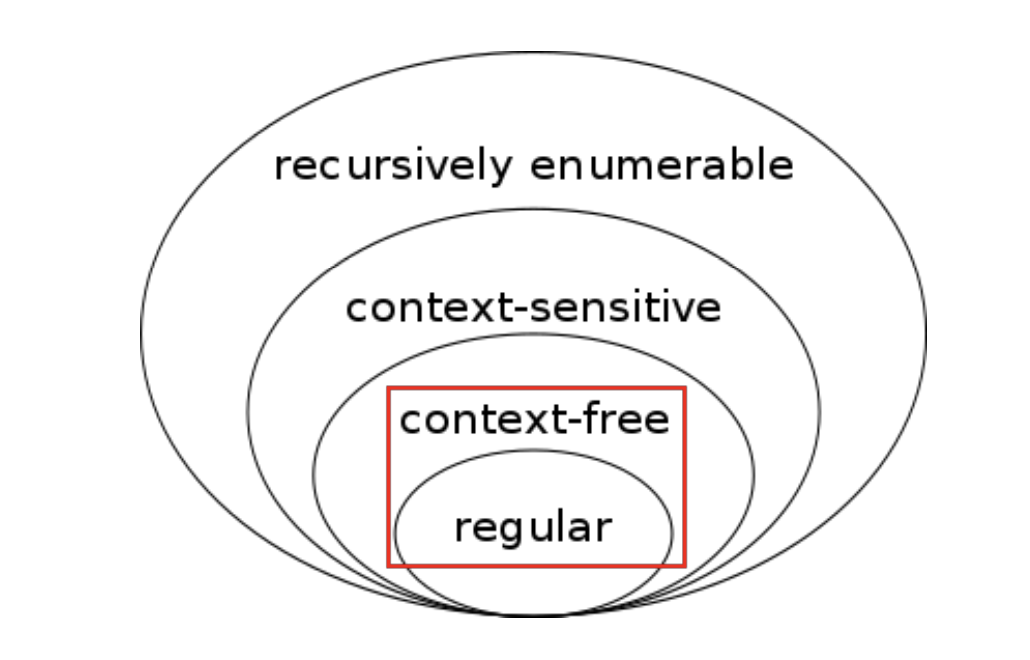
Pumping Lemma for Regular Languages
$Thm:$ $L=\{a^nb^n|n\geq 0\}$ 无法用正则表达式描述. 证明如下:
假设存在正则表达式 $r$ $s.t.$ $L(r)=L$ , 则存在有限状态自动机 $D(r): L(D(r))=L$ , 假设其状态数是 $k$ , 如果输入 $a^m\ (m> k)$ , 根据如下的图示:

$D(r)$ 也能接受 $a^ib^{i+j}$, 矛盾.
Pumping Lemma for Context-free Languages
$Thm$: $L=\{a^nb^nc^n|n\geq 0\}$ 无法用上下文无关文法描述. 证明 不会 略去.
4. 递归下降的 $LL$ 语法分析器
在无二义性的文法中, 每个句子对应唯一的一棵语法分析树. 有如下常见的文法:
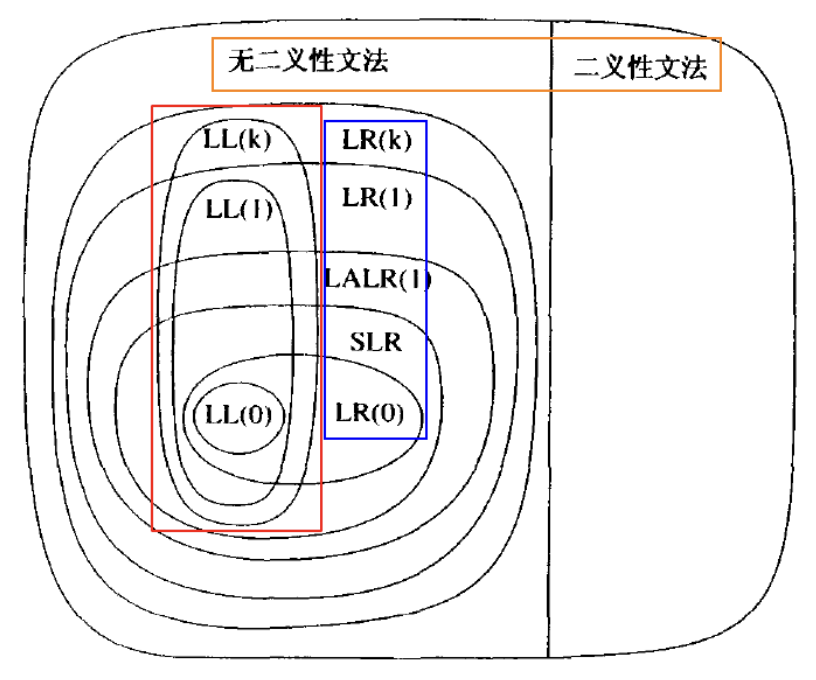
值得注意的是, 无论是常见的 $LL$ 还是 $LR$ 算法, 都无法处理二义性文法. 要处理二义性文法, 需要借助 $LL(*)/\text{ALLStar}$ 算法.
${\color{red}{L}}L(1)$ : 从左向右 ($\text{left to right}$) 读入词法单元
$L{\color{red}{L}}(1)$ : 构建最左推导 ($\text {leftmost}$) (总是选择最左边的非终结符进行展开)
$LL({\color{red}{1}})$ : 只需向前看一个输入符号便可确定使用哪条产生式
而 $LL(1)$ 语法分析器具有如下的四个特点:
- 自顶向下
- 递归下降
- 基于预测分析表
- 适用于 $LL(1)$ 文法
4.1. 自顶向下构建语法分析树
- 根节点是文法的起始符号 $S$
- 每个中间节点表示对某个非终结符应用某个产生式进行推导: 需要考虑
- 叶节点是词法单元流 $\omega\$$: 仅包含终结符号与特殊的文件结束符 $\$$ ($\text {EOF}$)
4.2. 递归下降的实现
递归下降可以这样实现: 为每个非终结符写一个递归函数 内部按需调用其它非终结符对应的递归函数, 下降一层 .

4.3. 预测分析表
预测分析表指明了每个**非终结符在面对不同的词法单元或文件结束符时, 该选择哪个产生式** (按编号进行索引) 或者报错 (空单元格)
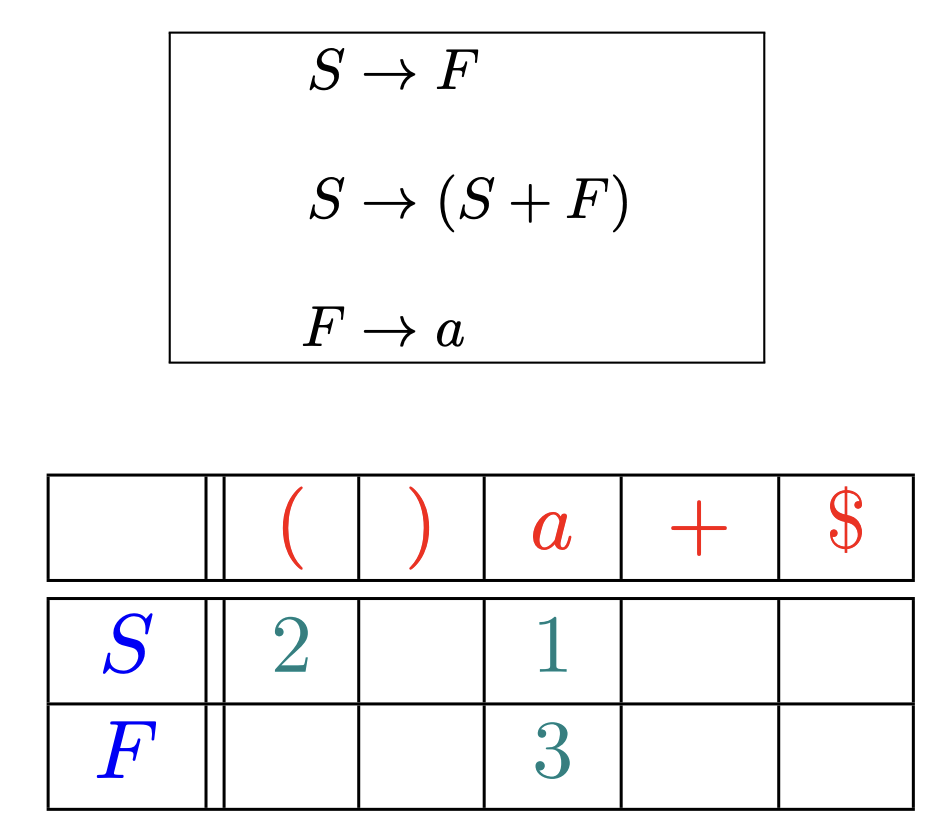
4.4. LL(1) 文法
$def:$ 如果文法 $G$ 的预测分析表是无冲突的, 则 $G$ 是 $LL(1)$ 文法.
其中, 无冲突指的是每个单元格里只有一个生成式 (编号). 对于当前选择的非终结符, 仅根据输入中当前的词法单元 (即 $LL(1)$ ) 即可确定需要使用哪条产生式. 这里需要介绍两个概念:
- $\text F\small \text{IRST}\normalsize(\alpha)$ 集合
- $\text F\small \text{OLLOW}\normalsize(A)$ 集合
1. $\text F\small \text{IRST}\normalsize(\alpha)$ 集合
$\text{F}\small \text{IRST}\normalsize (α)$ 是可从 $α$ 推导得到的句型的首个终结符号的集合. 形式化地, $\text F\small\text{IRST}\normalsize(α)$ 有定义如下.
$def: $ $\forall \alpha \in (T\cup N)^*$ ( $\alpha$ 是产生式的右部):
其中 $\beta \in (T\cup N)^*$.
考虑非终结符 $A$ 的所有产生式 $A → α_1, A → α_2, . . . , A → α_m$, 如果它们对应的 $\text F\small\text {IRST}\normalsize(α_i)$ 集合互不相交, 则只需查看当前输入词法单元, 即可确定选择哪个产生式 (或报错).
为了计算 $\text{F}\small\text{IRST}\normalsize(\alpha)$ , 先计算 $\alpha$ 中每个符号 $X$ 的 $\text F\small \text{IRST}\normalsize(X)$ 集合

不断应用上面的规则, 直到每个 $\text F\small \text{IRST}\normalsize(X)$ 都不再变化. 再计算每个符号串 $\alpha$ 的 $\text F\small \text{IRST}\normalsize(\alpha)$ 集合. 首先将 $\alpha$ 中的第一个符号 $X$ 取出来, 则:
此时有:
最后, 如果 $\epsilon \in L(\alpha)$ , 则将 $\epsilon$ 加入 $\text F\small \text{IRST}\normalsize(\alpha)$.
下面给出计算 $\text F\small \text{IRST}$ 集合的一个例子. 要特别注意什么时候要加入 $\epsilon$ 而什么时候不要.

2. $\text F\small \text{OLLOW}\normalsize(A)$ 集合
$\text F\small\text{OLLOW}\normalsize(A)$是可能在某些句型中紧跟在非终结符 $A$ 右边的终结符的集合. 形式化地, $\text F \small\text{OLLOW}\normalsize(A)$ 有定义如下.
$def:$ 对于任意的 (产生式的左部) 非终结符 $A \in N$ :
其中 $\beta, \gamma\in (T\cup N)^*$.
考虑产生式 $A \to \alpha$. 特别地, 如果从 $\alpha$ 可能推导出空串 $({\color{red}{ \alpha \overset * \Rightarrow \epsilon}})$, 则只有当当前词法单元 $t \in \text F \small\text{OLLOW}\normalsize(A)$ , 才可以选择该产生式.
为了给每个非终结符 $X$ 计算 $\text F\small \text{OLLOW}\normalsize(X)$ 集合, 需要考虑如下的算法:

不断应用上面的规则, 直到每个 $\text F\small \text{OLLOW}\normalsize(X)$ 都不再变化.
下面给出构建 $\text F\small \text{OLLOW}$ 集合的一个例子.

4.5. 计算预测分析表
现在我们已经有了 $LL(1)$ 文法的 $\text F \small \text {IRST}$ 与 $\text F \small\text{OLLOW}$ 集合, 那么如何根据 $\text F \small \text {IRST}$ 与 $\text F \small\text{OLLOW}$ 集合计算给定文法 $G$ 的预测分析表 ?
对于每条产生式 $A \to \alpha$ 与终结符 $t$, 如果:
则在表格 $[A,t]$ 中填入 $A \to \alpha$ (的编号).
让我们重新审视 $LL(1)$ 文法的定义.
$def:$ 如果文法 $G$ 的预测分析表是无冲突的, 则 $G$ 是 $LL(1)$ 文法.
4.6. LL(0) 文法
$LL(0)$ 是非递归的预测分析算法.
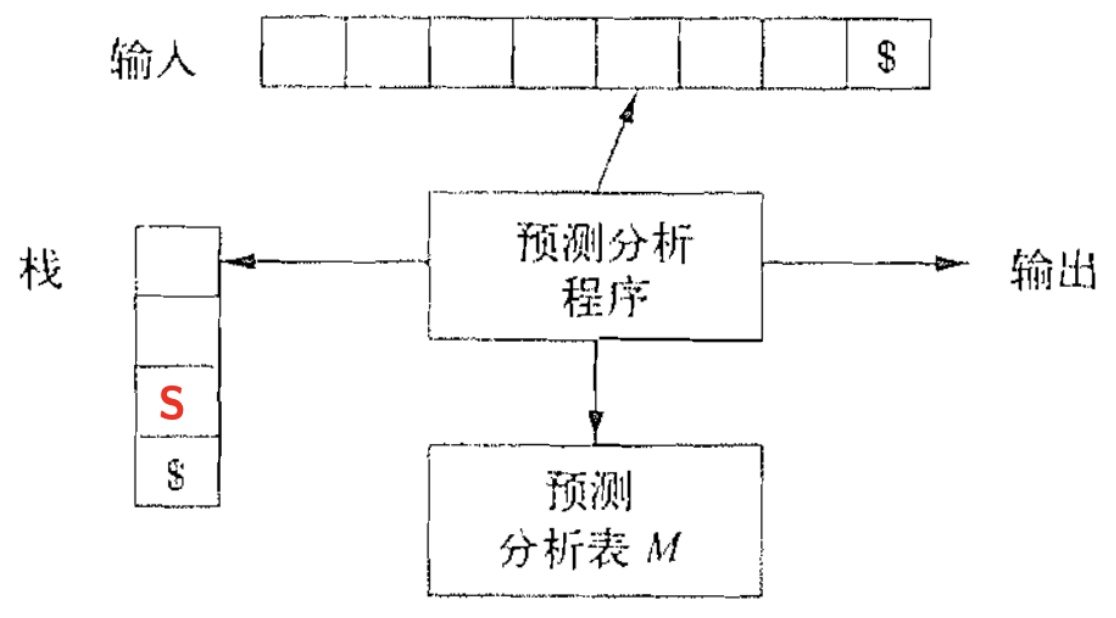

4.7. 处理非 LL(1) 文法
如果文法 $G$ 不是 $LL(1)$ 文法, 但仍然想使用 $LL(1)$ 语法分析器来处理. 我们没有好的办法, 只能将该文法转换成 $LL(1)$ 文法. 有两种常见的方法:
- 消除左递归
- 提取左公因子
以表达式的文法为例:
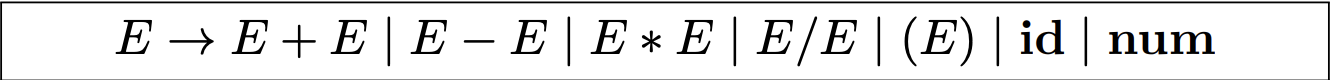
1. 消除左递归
左递归包括直接左递归 (Direct Left Recursion) 和间接左递归 (Indirect Left Recursion)
一个例子
在 2.2 中, 我们讲到了将上述文法改成如下的文法, 可以消除二义性, 但是不能改变左递归性.

$LL(1)$ 不能处理左递归的文法, 因为 $E$ 在不消耗任何词法单元的情况下, 直接递归调用 $E$ 本身, 造成了死循环. 一个可能的解决方法是, 将上述的文法改成右递归, 如下:
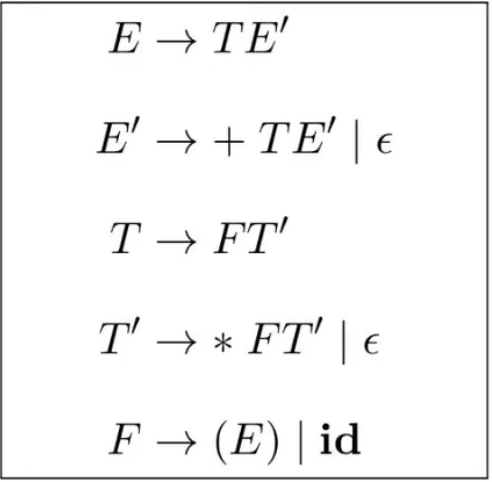
并且在此基础上构建其预测分析表:
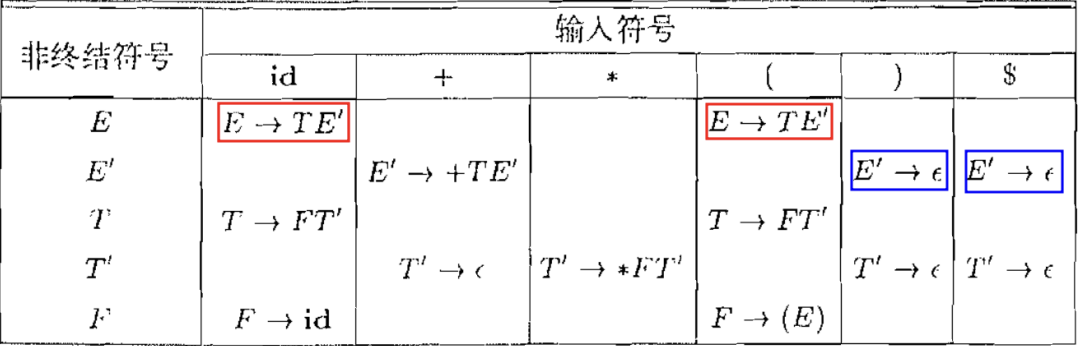
但是这样改造的代价是, 文法变得非常复杂, 而且失去了原本直观的含义.
消除直接左递归
对于这样直接左递归 $A\to A\alpha\ |\ \beta$ , 可以改成这样的右递归:
更加一般地, 行如下的左递归 (其中, $\beta_i$ $(1\leq i \leq n)$ 不以 $A$ 开头) :
可以统一地构造出这样的右递归写法:
消除间接左递归
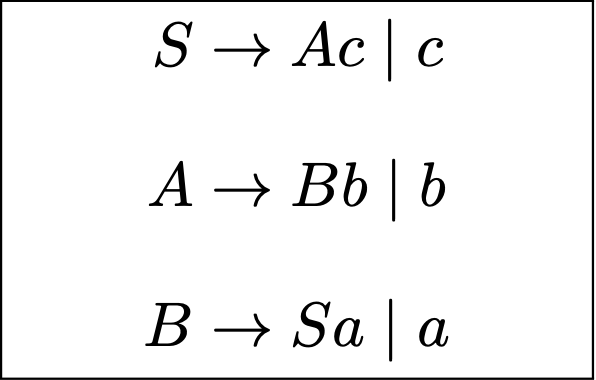 $$
S\Rightarrow Ac \Rightarrow Bbc \Rightarrow Sabc
$$
对于间接左递归, 我们有如下的消除算法:
$$
S\Rightarrow Ac \Rightarrow Bbc \Rightarrow Sabc
$$
对于间接左递归, 我们有如下的消除算法:

算法的成立条件是:
- 文法中不存在环 (形如 $A \overset * \Rightarrow A$ 的推导)
- 文法中不存在 $\epsilon$ 产生式 (形如 $A \to \epsilon$ 的产生式)
2. 提取左公因子 (Left-Factoring)
在 2.2 中, 我们讲到了提取左公因子无助于消除文法二义性. 但是 ANTLR4 可以处理有左公因子的文法. (开挂属于是)
5. Adaptive $\small LL(*)$ 语法分析算法
可以从这篇论文中了解到 $\text{Adaptive}\ LL(*)$ 设计的更多细节, 但是这片论文运用了大量的形式化方法, 我
看不懂目前还看不懂.这一算法又被缩写成 $ALLStar$ 算法
两个主题:
- 掌握: 处理表达式优先级
- 了解: 处理语法错误
5.1. ALL(*) 处理表达式优先级
ANTLR4 ( 使用了 $ALL(*)$ 算法的分析器) 的四个优势:

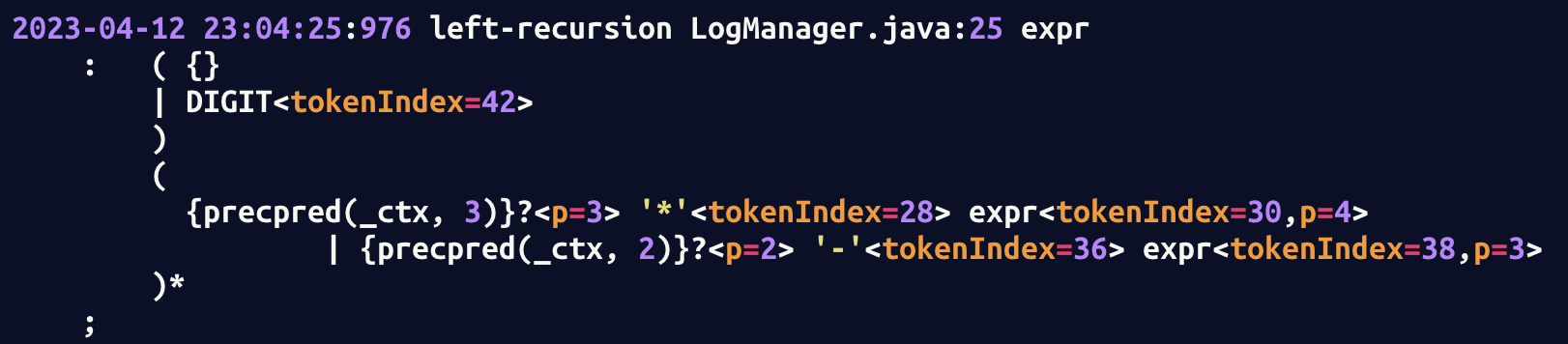
$ALL(*)$ 根据 g4 文件中定义的优先级, 将文法大致改写成如下的形式 (经简化):
1 | expr[int _p]: |
- 想要该运算符实现左结合, 则右侧递归时选择优先级上升:
<PRIORITY_1> + 1 - 想要实现右结合, 则优先级不变
 $$
\begin{align}
& \text{For } left\mbox-associative \ \text{operators, the right operand gets}\ \mathbf{one\ more}\ \text {precedence level than the operator itself.}\\
& \text{For } right\mbox-associative \ \text{operators, the right operand gets}\ \mathbf{the \ same}\ \text {precedence level than the operator itself.}
\end{align}
$$
$$
\begin{align}
& \text{For } left\mbox-associative \ \text{operators, the right operand gets}\ \mathbf{one\ more}\ \text {precedence level than the operator itself.}\\
& \text{For } right\mbox-associative \ \text{operators, the right operand gets}\ \mathbf{the \ same}\ \text {precedence level than the operator itself.}
\end{align}
$$
5.2. ALL(*) 处理错误
6. 不断规约的 LR 语法分析器
这篇文章介绍了关于LR的基本知识
自底向上的、 不断归约的、 基于句柄识别自动机的、 适用于$LR$ 文法的、 $LR$ 语法分析器
- $LL(k)$ 的弱点: 在仅看到右部的前 k 个词法单元时就必须预测要使用哪条产生式
- $LR(k)$ 的优点: 看到与正在考虑的这个产生式的整个右部对应的词法单元之后再决定
自底向上构建语法分析树
- 根节点是文法的起始符号 $S$
- 每个中间非终结符节点表示使用它的某条产生式进行归约
- 叶节点是词法单元流 $w$$ 仅包含终结符号与特殊的文件结束符 $

不妨查看蚂蚁老师的视频.