Support Vector Machines

CS › Machine Learning

1. Perceptron

1.1. Intro

从统计学的观点来看, 机器学习的目的是得到映射 $x\to y$. 这里必须要区分的四个概念是:

  • 类的先验概率: $p(y=i)$
  • 样本的先验概率: $p(\boldsymbol x)$.
  • 类的条件概率 (likely): $p(\boldsymbol x |y=i)$
  • 后验概率: $p(y=i|\boldsymbol x)$

根据这四个概念的组合, 统计机器学习方法也可以分成两类 (从概率框架的角度)

  • Generative Models: 估计 $p(\boldsymbol x |y=i)$ 和 $p(y=i)$, 然后用 $\text{Bayes}$ 公式求 $p(y=i|\boldsymbol x)$
  • Discriminative Models: 直接估计 $p(y=i|\boldsymbol x)$. 为了刻画这一现象, 我们提出一个新的名词: Discriminant function, 它是一个并不假设概率模型而直接将各类分开的边界. (无法反映训练数据本身的特性, 能力有限, 其只能告诉我们分类的类别.)

1.2. Perceptron

Binary Classification Problem 可以看作是在特征空间上对类别进行划分的任务. 很自然地, 我们需要一个超平面来进行划分. Perceptron 就是这样的超平面:

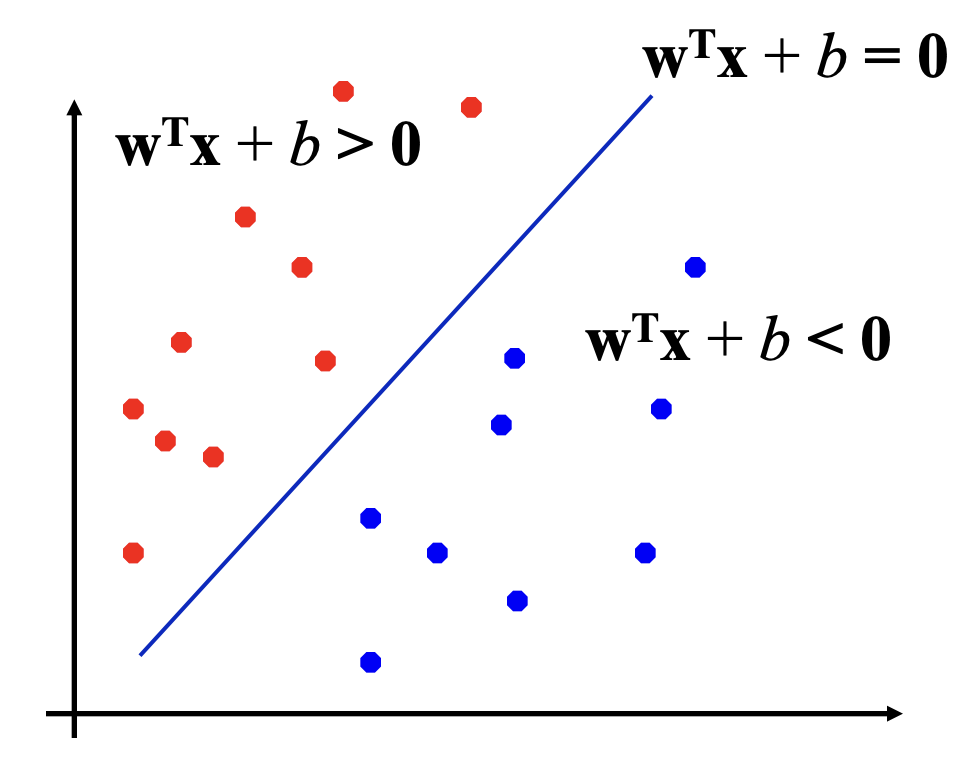
$$\Gamma: \boldsymbol w^{\mathbf{T}} \boldsymbol x+ b=0 $$

上图中的0不应该是黑体, 有误.

其中, 判别函数 $f(x)$ 可以为:

$$f(\boldsymbol x)=\operatorname{sign}\left(\boldsymbol w^{\mathbf{T}} \boldsymbol x+ b\right) $$

关于 Binary Classification 可以查看笔者的另外一篇数学建模笔记

然而, 能够将训练样本分开的超平面很多. 我们很自然地也想从中找到最合适的超平面

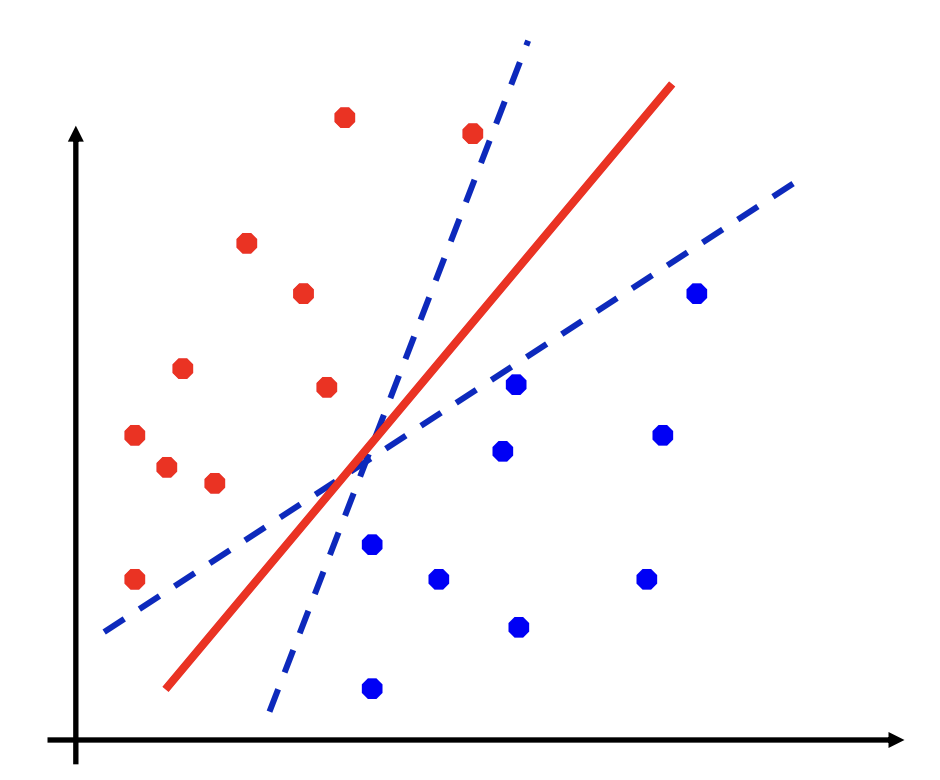
我们发现, 如果可以定量地刻画, 我们希望这个超平面在所有样本的中间, 这样有更好的鲁棒性. 在这样的前提下, 我们引入了 SVM 的概念.

2. Linear SVM

2.1. Margin and Support Vectors

假设有分界超平面: $\Gamma: \boldsymbol w^{\mathbf{T}} \boldsymbol x+ b= 0$

  • (样本的) margin 指的是某一个样本到 $\Gamma$ 的距离
  • 支持向量指的是在样本全体中, 距离 $\Gamma$ 最近的样本. (一个样本就是一个向量, 支持向量对于超平面的确定具有决定性作用, 因此叫支持向量.)
  • SVM的任务是使得支持向量到 $\Gamma$ 的距离尽可能大.

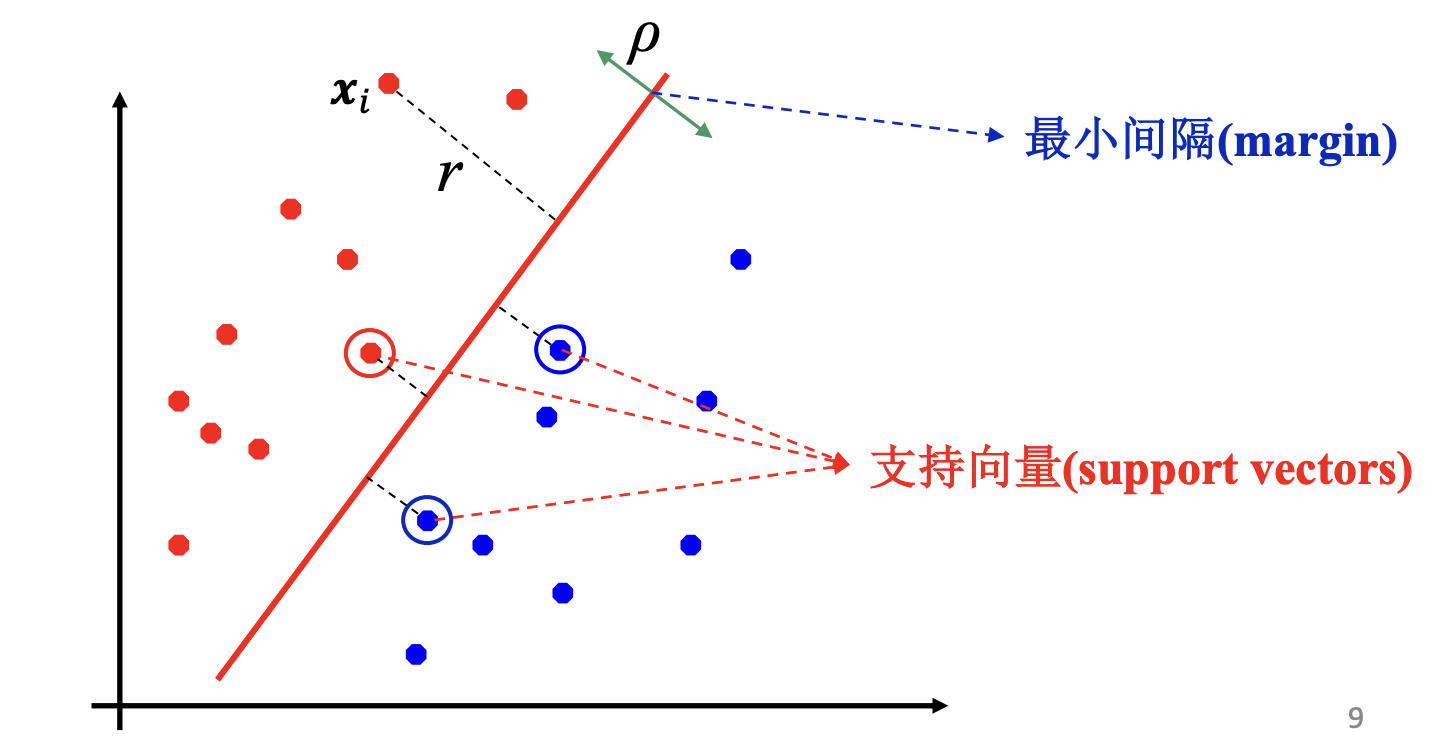
根据初等代数的手段, 很容易得 $\boldsymbol x_i$ 的 margin 为:

$$\frac{|\boldsymbol w^{\mathbf{T}} \boldsymbol x+b|}{\|\boldsymbol w\|} $$

formally, SVM的目标是计算如下的值:

$$\begin{align} &\underset{\boldsymbol{w}, b}{\operatorname{argmax}}\left(\min _{i}\left(\frac{\left|\boldsymbol{w}^{\textbf T} \boldsymbol{x}_{i}+ b\right|}{\|\boldsymbol{w}\|}\right)\right) \\ =\quad&\underset{\boldsymbol{w}, b}{\operatorname{argmax}}\left(\min _{i}\left(\frac{y_{i}\left(\boldsymbol{w}^{\textbf T} \boldsymbol{x}_{i}+ b\right)}{\|\boldsymbol{w}\|}\right)\right) \quad\text{subject to }y_i\in \left\{0,1\right\}\\ =\quad&\underset{\boldsymbol{w}, b}{\operatorname{argmax}}\left(\frac{1}{\|\boldsymbol{w}\|} \min _{i}\left(y_{i}\left(\boldsymbol{w}^{\textbf T} \boldsymbol{x}_{i}+ b\right)\right)\right) \end{align} $$

2.2. Optimizations-I

代数上, 我们发现这个式子太宽泛. 最起码, 我们至少可以规定一下 $\|\boldsymbol w\|$ 的值, 来简化这样的式子 (比值的约束关系). 我们考虑进行这样的限定

$$\min _{i}\left(y_{i}\left(\boldsymbol{w}^{\textbf T} \boldsymbol{x}_{i}+ b\right)\right)=1 $$

那么此时有

$$\underset{\boldsymbol{w}, b}{\operatorname{argmax}}\left(\frac{1}{\|\boldsymbol{w}\|} \min _{i}\left(y_{i}\left(\boldsymbol{w}^{\textbf T} \boldsymbol{x}_{i}+ b\right)\right)\right)= \underset{\boldsymbol{w}, b}{\operatorname{argmax}}\left(\frac{1}{\|\boldsymbol{w}\|} \right) $$

$i.e.$

$$\begin {align} \underset{\boldsymbol{w}, b}{\operatorname{argmin}}\left(\frac{1}2\boldsymbol w^{\textbf T}\boldsymbol w \right)\quad s.t.\quad \forall i:y_{i}\left(\boldsymbol{w}^{\textbf T} \boldsymbol{x}_{i}+b\right) \geq 1 \end {align} $$

为了计算出这样的 $\boldsymbol{w}, \boldsymbol b$, 我们很自然地考虑 $\text{Lagrange}$ 乘数法. 考虑

$$L(\boldsymbol{w}, b, \boldsymbol{a})=\frac{1}{2} \boldsymbol{w}^\textbf{T} \boldsymbol{w}-\sum_{i=1}^{n} a_{i}\left(y_{i}\left(\boldsymbol{w}^{\textbf{T}} \boldsymbol{x}_{i}+ b\right)-1\right) $$
  • $\text{Subject to } a_i\ge 0$

我们得到这样的代数恒等式

$$\begin{align} \frac{\partial L}{\partial \boldsymbol{w}}=\mathbf{0} &\implies \boldsymbol{w}=\sum_{i=1}^{n} a_{i} y_{i} \boldsymbol{x}_{i} \\ \frac{\partial L}{\partial b}= 0 &\implies 0=\sum_{i=1}^{n} a_{i} y_{i} \end{align} $$

我们再将这两个式子回代, 得到

$$\tilde{L}(\boldsymbol{a})=\sum_{i=1}^{n} a_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} a_{i} a_{j} y_{i} y_j \boldsymbol{x}_{i}^\textbf{T} \boldsymbol{x}_{j} $$

实际上, 我们这里得到的条件又被称为 $\text{Karush-Kuhn-Tucker}$ 条件 (KKT). 它是对普通 $\text{Lagrange Multiplier}$ 方法的泛化. 一般而言, KKT条件不是充分必要的; 但在原始 SVM 问题里, 这些条件对于确定最优解即是充分又必要的.

2.3. Dual Forms

我们在上面提到了**原始 SVM **, 这是一个新的概念. 实际上,

  • 在原来的空间 (即输入空间) 中, 变量是 $\boldsymbol {x}_i$, 称为 SVM 的原始形式 (primal form)
  • 现在的问题里面: 变量是 $a_i$, 即拉格朗日乘子, 称为对偶空间 (dual space)
    • 对偶空间完成优化后, 得到最优的 $\boldsymbol a$, 可以得到原始空间中的最优解 $\boldsymbol w$

所以, 我们现在要求的是:

$$\arg\max_{\boldsymbol a} \tilde{L}(\boldsymbol{a}) $$

现在已经变成单变量问题, 求解变得很 trivial.

2.4. Optimizations-II

上面是从代数的角度进行优化. 那么从含义上看, 如果我们允许 SVM 犯一些错误, 但是能够在别的程度上大幅提高效果 (比如说显著提高 margin), 那么也是完全可以接受的.

我们于是提出 soft margin 的概念, 并对关键的假设进行如下的更正.

$$y_{i}\left(\boldsymbol{w}^{\boldsymbol{T}} \boldsymbol{x}_{i}+b\right) \geq 1 \rightarrow y_{i}\left(\boldsymbol{w}^{\boldsymbol{T}} \boldsymbol{x}_{i}+b\right) \geq 1-\xi_{i} $$

其中, $\xi_i$ 称为松弛变量 (slack variable), 即允许犯的错误.

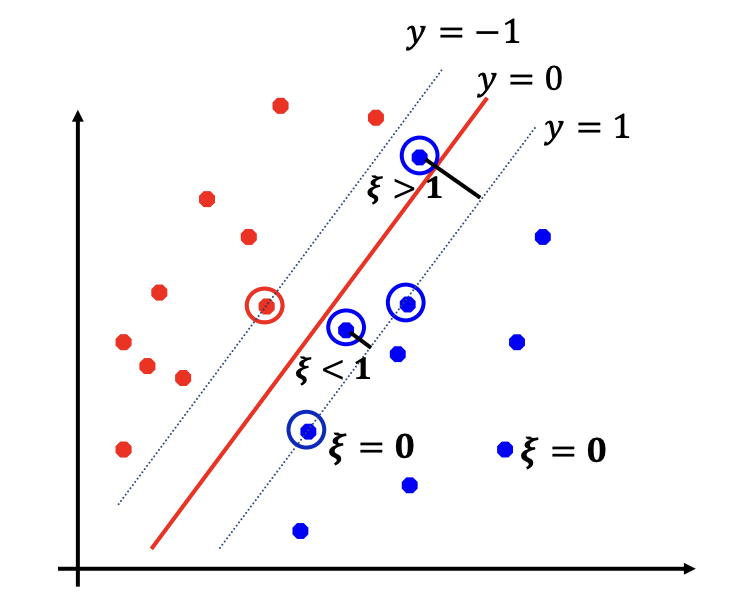
明显, 我们对于犯错要进行合理的惩罚. 我们将在原始空间和对偶空间中分别考察.

对于原始空间, 我们所求的 $\xi$ 为

$$\xi \in \underset{\boldsymbol{w}, b, \xi}{\operatorname{argmin}} \left(\frac{1}{2} \boldsymbol{w}^{\textbf T} \boldsymbol{w}+C \sum_{i=1}^{n} \xi_{i}\right) \quad \left( y_{i}\left(\boldsymbol{w}^{\textbf T} \boldsymbol{x}_{i}+b\right) \geq 1-\xi_{i} \quad\xi_{i} \geq 0 \right) $$

这里的 $C$ 为正则化参数, 可以由我们自己选择, 来刻画我们允许 SVM 犯错的程度.

对于对偶空间:

$$\underset{\boldsymbol{a}}{\operatorname{argmax}} \sum_{i=1}^{n} a_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} a_{i} a_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\textbf T} \boldsymbol{x}_{j} \quad s.t. \quad C \geq a_{i} \geq 0 \quad \sum_{i=1}^{n} a_{i} y_{i}=0 $$

一个有趣的发现是, 对偶形式只依赖于内积, $\xi$ 在这里消失了.

3. Non-linear SVM

3.1. Dimensionality Augmentation

实际上, 数据集不总是 线性可分 的

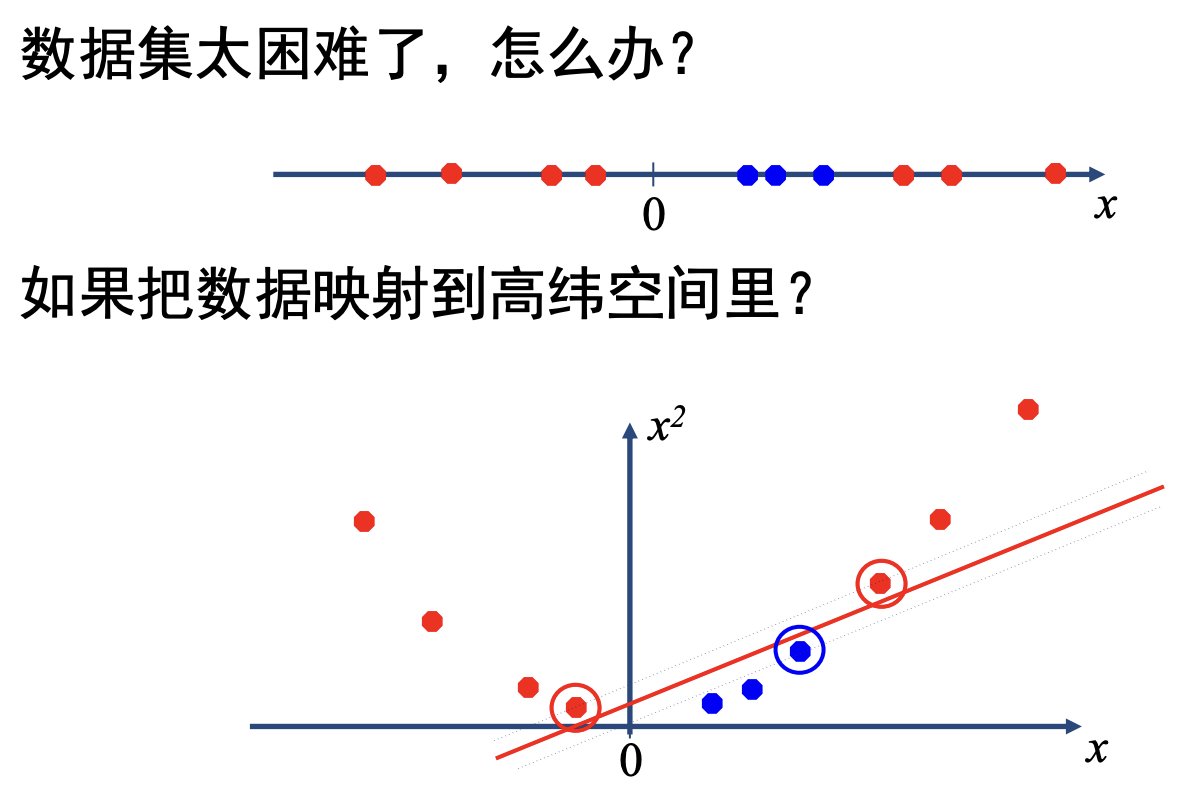
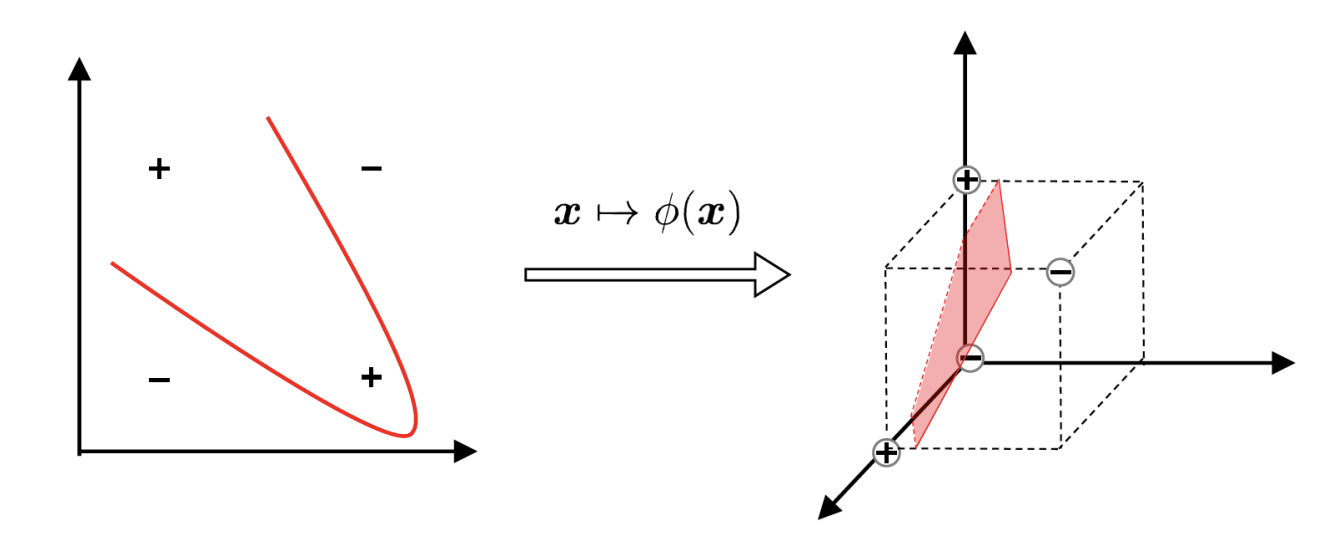
我们可以考虑将样本从原始空间映射到一个更高维的特征空间, 使样本在这个特征空间内线性可分. 实际上, 如果原始空问是有限维 (属性数有限), 那么一定存在一个高维特征空间使样本可分. 也就是说:

对于两个向量 $\boldsymbol x,\boldsymbol y\in\mathbb R^d$, 一个非线性函数 $K(\boldsymbol x,\boldsymbol y)$, 对于**满足某些条件的函数** $K$, 一定存在一个映射 (mapping) $\phi:\mathbb R^d\to \Phi$, 使得

$$\forall\boldsymbol x,\boldsymbol y:K(\boldsymbol x,\boldsymbol y)=\phi(\boldsymbol x)^\textbf T\phi(\boldsymbol y) $$
  • 非线性函数 $K$ 表示两个向量的相似程度, 其等价于 $\phi$ 里面的内积.
  • $\Phi$ 为特征空间 (feature space), 可以是有限维的空间，但也可以是无穷维的空间 (infinite dimensional Hilbert space)

具体来说, 上面的 某些条件 指的是:

  • 你要熟悉泛函分析😭

  • 必须存在特征映射 (feature mapping), 才可以将非线性函数表示为特征空问中的内积

  • Mercer’s condition (Mercer条件，是充分必要的):

    • 对任何满足 $\displaystyle \int g^{2}(\boldsymbol{u}) d \boldsymbol{u}<\infty$ 的非零函数 (平方可积函数), 对称函数 $K$ 满足条件:
      $$\iint K(\boldsymbol{u}, \boldsymbol{v}) g(\boldsymbol{u}) g(\boldsymbol{v}) d \boldsymbol{u} d \boldsymbol{v} \geq 0 $$

  • 另一种等价形式: 对任何一个样本集合 $\left\{x_{1}, \ldots, x_{n}\right\}, x_{i} \in \mathbb{R}^{d}$, 如果短阵 $K=\left[K_{i j}\right]_{i}$ (矩阵的第 $i$ 行, 第 $j$ 列元素 $K_{i j}=K\left(x_{i}, x_{j}\right)$ ) 总是半正定的, 那么函数K满足Mercer条件.

3.2. Kernel SVM

下面的定义已经变得非常自然, 尤其是我们解释清楚 Kernel 的作用之后.

  • Kernel Function: $K$
  • Dual Form: $\displaystyle \underset{\boldsymbol{a}}{\operatorname{argmax}} \sum_{i=1}^{n} a_{i}-\frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} a_{i} a_{j} y_{i} y_{j} K\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)$
  • Separating Hyperplane: $\displaystyle \boldsymbol{w}=\sum_{i=1}^{n} a_{i} y_{i} \phi\left(\boldsymbol{x}_{i}\right)$
  • How to predict:
$$\boldsymbol{w}^{\textbf T} \phi(\boldsymbol{x})=\boldsymbol{\phi}(\boldsymbol{x})^{\textbf T}\left(\sum_{i=1}^{n} a_{i} y_{i} \phi\left(\boldsymbol{x}_{i}\right)\right)=\sum_{i=1}^{n} a_{i} y_{i} K\left(\boldsymbol{x}, \boldsymbol{x}_{i}\right) $$

一些常见的 Kernel 有:

  • Linear Kernel: $K(\boldsymbol x,\boldsymbol y)=\boldsymbol x^\textbf T\boldsymbol y$
  • RBF (radial basis function) / $\text{Gaussian}$ Kernel: $K(\boldsymbol{x}, \boldsymbol{y})=\exp \left(-\gamma\|\boldsymbol{x}-\boldsymbol{y}\|^{2}\right)$
  • Polynomial Kernel: $K(\boldsymbol{x}, \boldsymbol{y})=\left(\gamma \boldsymbol{x}^{\textbf T} \boldsymbol{y}+c\right)^{d}$

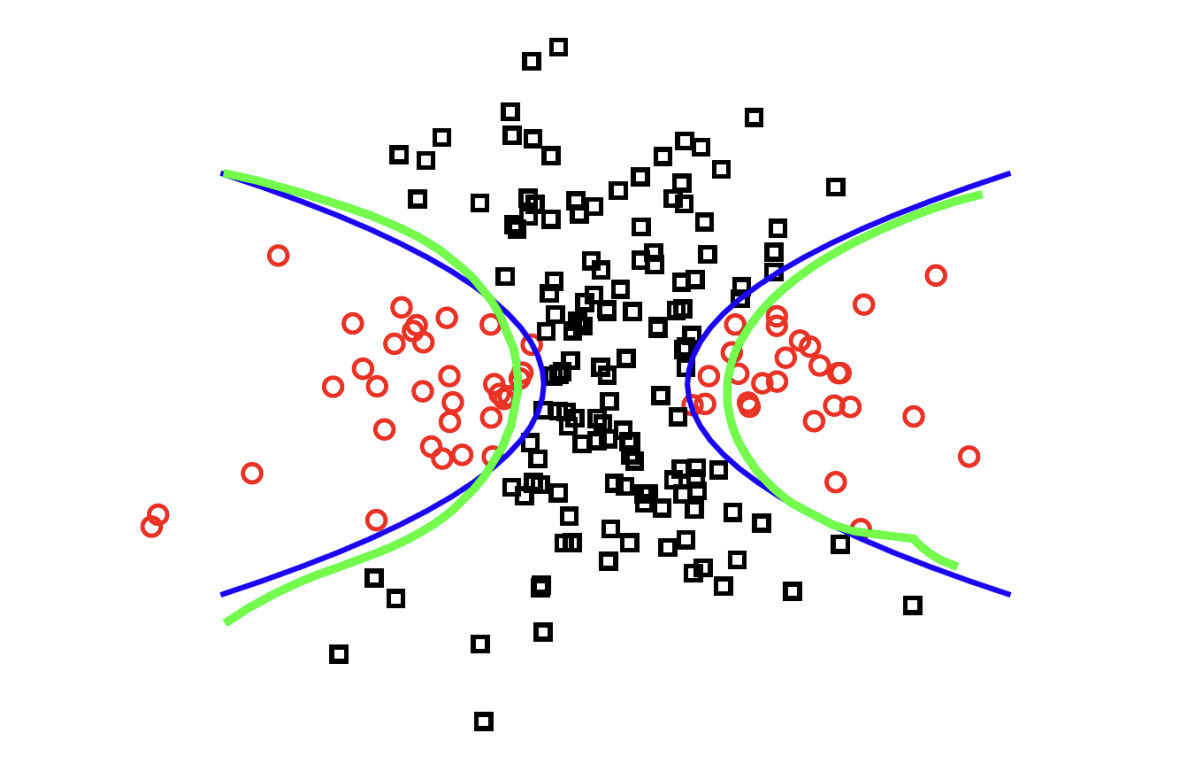
下图是一个 RBF Kernal 的例子. 其中蓝色为真实边界, 绿色为使用 RBF Kernal SVM 得到的边界.

3.3. Hyper-parameter

如何决定 $C,\gamma$ 等参数

  • 必须给定这些参数的值, 才能进行SVM学习, SVM本身不能学习这些参数
  • 称为超参数 (hyper-parameter)
  • 对SVM的结果有极大的影响

用交叉验证在训练集上学习

  • 在训练集上得到不同参数的交叉验证准确率
  • 选择准确率最高的超参数的数值

4. Multiclass SVM, MSVM

MSVM有两种基本思路: 1-vs-1 和 1-vs-rest. 假设我们希望结果为 $C$ 个类

4.1. one-vs.-one

设计 $\displaystyle \binom{C}{2}$ 个分类器, 用 $i$ 和 $j$ 两类 ($i>j$) 的训练数据进行学习. 显然在所有的分类器中, 每个类会出现 $C-1$ 次.

  • 对任何一个测试样本 $\boldsymbol x$ 的 $\displaystyle\binom{C}{2}$ 个结果进行投票.
  • 对每个分类器采用其二值输出, 即 $\operatorname{sign}(f_i(\boldsymbol x))$

4.2. one-vs.-rest

设计 $C$ 个分类器, 第 $i$ 个分类器用类做正类, 把其他所有 $C-1$ 个类别的数据合并在一起做负类.

  • 和交叉验证的步骤有些类似
  • 每个新的分类起输出真实值, 即 $f_i(\boldsymbol x)$

$f_i(\boldsymbol x)$ 的实数输出可以看成是属于第 $i$ 类的“信心”(confidence), 最终选择信心最高的那个类为输出.

$$\arg\max_if_i(\boldsymbol x) $$