Special Counting Sequences

1. Catalan Numbers

1.1. Definition

$\textbf{Definition}$: The Catalan number $C_n$ if given by the formula

$$C_n=\frac{1}{n+1}\binom{2n}{n}$$

1.2. Applicable Combinatorial Structures

Preliminary problem: How many ways are there to walk from $(0,0)$ to $(n,n)$ in a $n\times n$ grid, where each step is either to the right or up?

This is a typical combinatorial problem. Since there are $2n$ steps in total, and we need to choose $n$ steps to go up, so the total number of ways is $\binom{2n}{n}$.

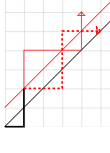
However, if we add another condition that the path should not cross (or touch) the line $y=x-1$, then the number of ways is equivalent to the following:

“How many ways are there to walk from $(0,1)$ to $(n,n)$ in a $n\times n$ grid, where each step is either to the right or up, and the path never crosses the diagonal?”

Since the first step can only be to the up

Now if we consider the symmetry point of $(0,1)$ ($i.e.$ $(1, 0)$) with respect to the diagonal: $y=x$, then the problem is equivalent to the following:

1.3. Recurrence Relation

1. $C_n = \displaystyle\sum_{i=0}^{n-1}C_iC_{n-1-i}$

Pf. From the perspective of combinatorics identity, by induction,

$$\begin{aligned} C_n &= \frac{1}{n+1}\binom{2n}{n}\\ &= \frac{1}{n+1}\left(\binom{2n-1}{n}+\binom{2n-1}{n-1}\right)\\ &= \frac{1}{n+1}\left(C_{n-1}+C_{n-2}\right)\\ &= \frac{1}{n+1}\left(\displaystyle\sum_{i=0}^{n-2}C_iC_{n-2-i}+\displaystyle\sum_{i=0}^{n-2}C_{i+1}C_{n-1-i}\right)\\ &= \frac{1}{n+1}\left(C_0C_{n-2}+C_{n-1}C_0+\displaystyle\sum_{i=1}^{n-2}C_iC_{n-1-i}+C_{n-1}C_{n-1-n+1}\right)\\ &= \frac{1}{n+1}\left(\displaystyle\sum_{i=0}^{n-1}C_iC_{n-1-i}\right) \end{aligned}$$

From the perspective of combinatorics meaning, we can also prove this by the following method.

2. $C_n = \displaystyle\sum_{n_1+\ldots+n_l=n}\prod_{i=1}^{l}C_{n_i-1}$

2. Difference Sequences

tbd.

3. Stirling Numbers

tbd.