This blog mostly refers to the link from U-Iowa.
In this blog, we mainly focus on
- the language and semantics for SMT-lib Input / Output
- Specifications of background theories and logics
- related tools and utils.
SMT-lib language
This pdf is the latest SMT-lib v2.6 standard manual.
Theories & Logics
Theories
ArraysEx: Functional arrays with extensionality
FixedSizeBitVectors: Bit vectors with arbitrary size
Core: Core theory, defining the basic Boolean operators
FloatingPoint: Floating point numbers
Ints: Integer numbers
Reals: Real numbers
Reals_Ints: Real and integer numbers
Strings: Unicode character strings and regular expressions
Logics
SMT-LIB 2 scripts, which includes all the benchmarks available from the Benchmarks section, refer to one of the following sub-logics of the main SMT-LIB logic. The reason to have a (sub-)logic is pragmatic:
- to identify fragment of the main logic where it may possible to apply specialized and more efficient satisfiability techniques.
New logics are added to the standard opportunistically, once enough benchmarks are available for it.
Here is an overview of the logics listed below, ordered by inclusion. A link from a logic L1 to a logic L2 means that every formula of L1 is also a formula of L2. Click on the node to go to its description. Then, click on the logic’s name to see its specification in SMT-LIB format.
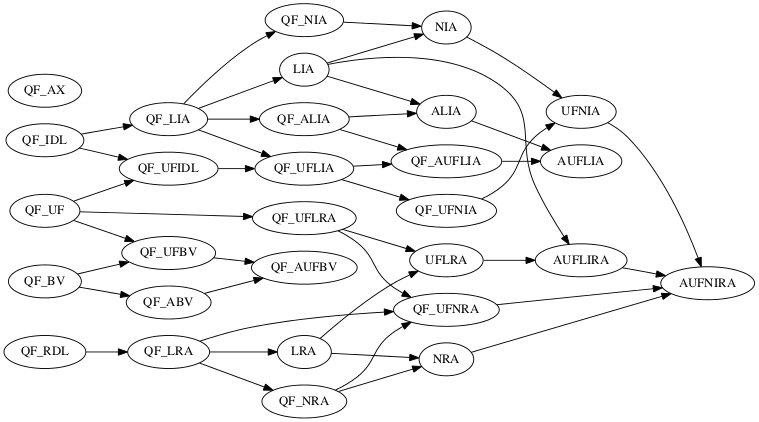
The logics have been named using letter groups that evoke the theories used by the logics and some major restriction in their language, with the following conventions:
QF for the restriction to quantifier free formulas
A/AX for the theory ArraysEx
BV for the theory FixedSizeBitVectors
FP (forthcoming) for the theory FloatingPoint
IA for the theory Ints (Integer Arithmetic)
RA for the theory Reals (Real Arithmetic)
IRA for the theory Reals_Ints (mixed Integer Real Arithmetic)
IDL for Integer Difference Logic
RDL for Rational Difference Logic
L before IA, RA, or IRA for the linear fragment of those arithmetics
N before IA, RA, or IRA for the non-linear fragment of those arithmetics
UF for the extension allowing free sort and function symbols
The reason for this, admittedly idiosyncratic, nomenclature is mostly historical. Also historical is the fact that some logics impose further restrictions on the language. For instance, in the ALIA logics the only array sort allowed is (Array Int Int), whereas in some A*IRA logics the only array sort allowed are (Array Int Real) and (Array Int (Array Int Real)). This is why, for instance, QF_AX is not a sublogic of QF_AUFLIA or QF_ABV. Finally, benchmarks are typically classified by the smallest logic they belong to. One consequence of this is that we do not have a logic such as RA here, for instance, since an RA benchmark belongs to either LRA or NRA.
Detailed Explanations of Logcis
**Note:**The listing below is currently incomplete. More will be added later.
[Logic declarations for Version 1.2 of SMT-LIB, superseded by the ones below, are still available here but their use is deprecated.]
AUFLIA: Closed formulas over the theory of linear integer arithmetic and arrays extended with free sort and function symbols but restricted to arrays with integer indices and values.
AUFLIRA: Closed linear formulas with free sort and function symbols over one- and two-dimentional arrays of integer index and real value.
AUFNIRA: Closed formulas with free function and predicate symbols over a theory of arrays of arrays of integer index and real value.
LIA: Closed linear formulas over linear integer arithmetic.
LRA: Closed linear formulas in linear real arithmetic.
QF_ABV: Closed quantifier-free formulas over the theory of bitvectors and bitvector arrays.
QF_AUFBV: Closed quantifier-free formulas over the theory of bitvectors and bitvector arrays extended with free sort and function symbols.
QF_AUFLIA: Closed quantifier-free linear formulas over the theory of integer arrays extended with free sort and function symbols.
QF_AX: Closed quantifier-free formulas over the theory of arrays with extensionality.
QF_BV: Closed quantifier-free formulas over the theory of fixed-size bitvectors.
QF_IDL: Difference Logic over the integers. In essence, Boolean combinations of inequations of the form x - y < b where x and y are integer variables and b is an integer constant.
QF_LIA: Unquantified linear integer arithmetic. In essence, Boolean combinations of inequations between linear polynomials over integer variables.
QF_LRA: Unquantified linear real arithmetic. In essence, Boolean combinations of inequations between linear polynomials over real variables.
QF_NIA: Quantifier-free integer arithmetic.
QF_NRA: Quantifier-free real arithmetic.
QF_RDL: Difference Logic over the reals. In essence, Boolean combinations of inequations of the form x - y < b where x and y are real variables and b is a rational constant.
QF_UF: Unquantified formulas built over a signature of uninterpreted (i.e., free) sort and function symbols.
QF_UFBV: Unquantified formulas over bitvectors with uninterpreted sort function and symbols.
QF_UFIDL: Difference Logic over the integers (in essence) but with uninterpreted sort and function symbols.
QF_UFLIA: Unquantified linear integer arithmetic with uninterpreted sort and function symbols.
QF_UFLRA: Unquantified linear real arithmetic with uninterpreted sort and function symbols.
QF_UFNRA: Unquantified non-linear real arithmetic with uninterpreted sort and function symbols.
UFLRA:: Linear real arithmetic with uninterpreted sort and function symbols.
UFNIA: Non-linear integer arithmetic with uninterpreted sort and function symbols.
etc.
Benchmarks
StarExec is a cross web-based community logic solving service developed at the University of Iowa
Utils & Solvers
Here are numerous utils and tools related to SMT-lib.
Here are numerous SMT-solvers, but the most famous one currently is Microsoft z3.
Sth about z3
- Z3简介及在逆向领域的应用 [link]