Sentential Logic

MATH › Logic
$$\newcommand{\vD}{\vDash} \newcommand{\mS}{\mathcal S} \newcommand{\mE}{\mathcal E} \newcommand{\te}{\models=\!\mid} \huge\textbf{Sentential Logic} $$

这份笔记是用来记录数理逻辑的诸多定义和定理的, 以加强记忆. 所有的笔记都基于 A Mathematical Introduction to Logic

1. The Language of Sentential Logic

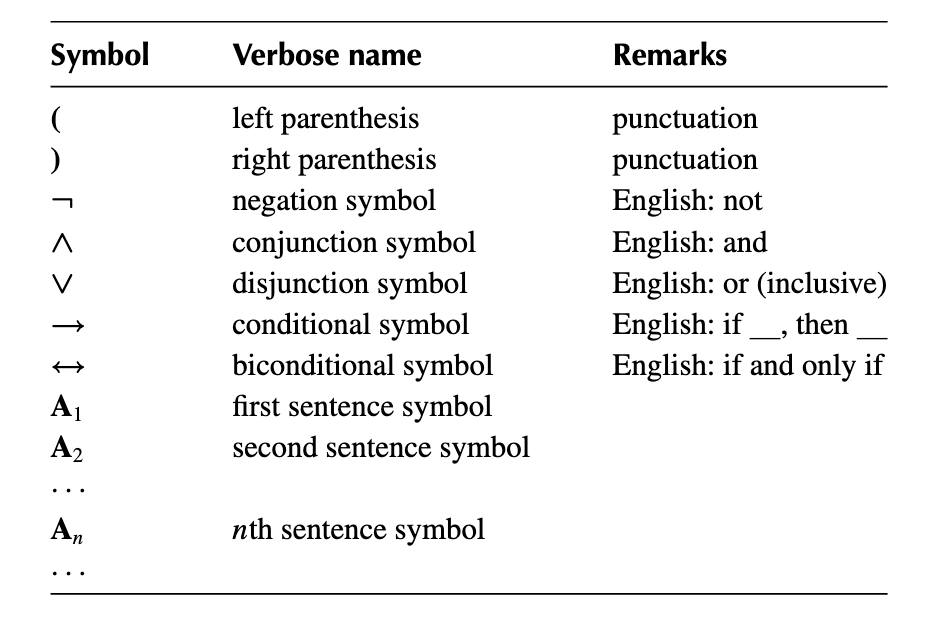
All Possible Symbols

Definition of sentential connective symbols (命题连接符)

$$\neg, \vee, \wedge, \to, \leftrightarrow $$

The 5 symbols above are called sentential connective symbols.

Definition of logical symbols

logic symbols are sentential connective symbols and parentheses

Definition: Sentence Symbol

The sentence symbols which are often denoted as $\mathbf{A_n}$ are the parameters (or nonlogical symbols).

Definition of Proposition Symbol

Proposition (命题) is what a sentence asserts.

命题就是肯定语句, 命题逻辑就是语句逻辑

We have assumed that no symbol is a finite sequence of other symbols. The purpose of this assumption is to assure that finite sequences of symbols are uniquely decomposable.

Definition of Expression

An expression is a finite sequence of symbols.

Definition of Well-formed Formulas

We want to define the well-formed formulas (wffs) to be the “grammatically correct” expressions; the nonsensical expressions must be excluded. The definition will have the following consequences:

  • Every sentence symbol is a wff.
  • If $\alpha$ and $\beta$ are wffs, then so are $(¬ α)$, $(α ∧ β)$, $(α ∨ β)$, $(α → β)$, and $(α ↔ β)$.
  • No expression is a wff unless it is compelled to be one by (a) and (b).

More precisely, A well-formed formula (or simply formula or wff ) is an expression that can be built up from the sentence symbols by applying some finite number of times the formula-building operations (on expressions) defined by the equations:

$$\begin{aligned} \mathcal{E}_{\neg}(\alpha) & =(\neg \alpha) \\ \mathcal{E}_{\wedge}(\alpha, \beta) & =(\alpha \wedge \beta), \\ \mathcal{E}_{\vee}(\alpha, \beta) & =(\alpha \vee \beta), \\ \mathcal{E}_{\rightarrow}(\alpha, \beta) & =(\alpha \rightarrow \beta), \\ \mathcal{E}_{\leftrightarrow}(\alpha, \beta) & =(\alpha \leftrightarrow \beta) .\end{aligned} $$

$\textbf{INDUCTION PRINCIPLE}$

If $S$ is a set of wffs containing all the sentence symbols and closed under all five formula-building operations, then $S$ is the set of all wffs.

2. Truth Assignments

Definition of Truth Values

A truth values set is $\{T, F\}$, where

$$\begin{aligned} & F: \text{called }\textit{falsity}\\ & T: \text{called }\textit{truth} \end{aligned} $$

Definition of Truth Assignment

A truth assignment $v$ for a set $\mathcal S$ of sentence symbols is a function

$$v :\mathcal S \to \{F, T\} $$

assigning either $T$ or $F$ to each symbol in $\mathcal S$.

Definition of Extension Set & Extension Assignment

Let $\mathcal {\bar S}$ be the set of wffs that can be built up from $\mathcal S$ by the five formula-building operations. ($\mathcal {\bar S}$ can also be characterized as the set of wffs whose sentence symbols are all in $\mathcal S$; see the remarks at the end of the preceding section.) We want an extension $\bar v$ of $v$,

$$\bar v : \bar S → \{F, T\}, $$

that assigns the correct truth value to each wff in $\mathcal {\bar S}$. It should meet the following conditions:

  1. $\forall A ∈ \mathcal S: \bar v(A) = v(A)$. (这也是为什么叫扩展 [extension])

$\forall \alpha,\beta \in \bar \mS$:

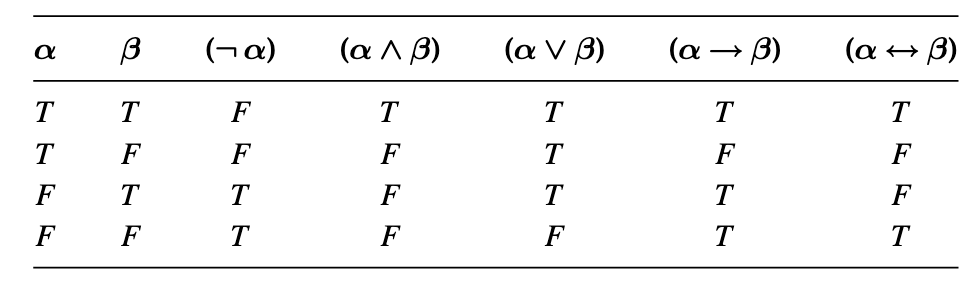
  1. $$\bar{v}((\neg \alpha))=\left\{\begin{array}{ll}T & \text { if } \bar{v}(\alpha)=F \\ F & \text { otherwise }\end{array}\right.$$
  2. $$\bar{v}((\alpha \wedge \beta))=\left\{\begin{array}{ll}T & \text { if } \quad \bar{v}(\alpha)=T \quad \text { and } \quad \bar{v}(\beta)=T \\ F & \text { otherwise. }\end{array}\right.$$
  3. $$\bar{v}((\alpha \vee \beta))=\left\{\begin{array}{ll}T & \text { if } \quad \bar{v}(\alpha)=T \quad \text { or } \quad \bar{v}(\beta)=T \text { (or both), } \\ F & \text { otherwise. }\end{array}\right.$$
  4. $$\bar{v}((\alpha \rightarrow \beta))=\left\{\begin{array}{ll}F & \text { if } \bar{v}(\alpha)=T \text { and } \bar{v}(\beta)=F, \\ T & \text { otherwise. }\end{array}\right.$$
  5. $$\bar{v}((\alpha \leftrightarrow \beta))=\left\{\begin{array}{ll}T & \text { if } \quad \bar{v}(\alpha)=\bar{v}(\beta) \\ F & \text { otherwise. }\end{array}\right.$$

$\textbf{THEOREM 12A}$

For any truth assignment $v$ for a set $S$ there is a unique function

$$v : \bar \mS \to \{F, T\} $$

meeting the aforementioned conditions 0–5.

$def:\textbf{Satisfy}$

A truth assignment $v$ satisfies a wff $\varphi$ iff. $\bar v(\varphi)=T$

Of course for this to happen, the domain of $v$ must contain all sentence symbols in $\varphi$.

Definition of Tautologically Implication

Consider a set of wffs $\Sigma$ and another wff $\tau$. $\Sigma$ tautologically implies $\tau $ (written $\Sigma\vD\tau$ ) iff. every truth assignment for the sentence symbols in $\Sigma$ and $\tau $ that satisfies every member of $\Sigma$ also satisfies $\tau $ .

$\Sigma$ can be thought of as hypotheses and $\tau$ can be thought of as a possible conclusion. This definition reflects our intuitive feeling that a conclusion follows from a set of hypotheses if the assumption that the hypotheses are true guarantees that the conclusion is true.

Definition of Tautology

consider a wff $\tau$, $\tau$ is a tautology iff. $\forall$ sentential symbol $\in\tau$, $\bar v(\tau)=T$.

two special cases are that

  • $\forall \tau:\emptyset\vD \tau$
  • $\forall \tau: \{A, \neg A\}\vD \tau$

If no truth assignment satisfies every member of $\Sigma$, then for any $\tau $ , it is vacuously true that $\Sigma \vD \tau$ .

Definition of Tautologically Equivalent

If $\Sigma$ is singleton $\{\sigma \}$, then we write "$\sigma\vD \tau $" in place of "$\{\sigma \} \vD \tau $". If both $\sigma \vD \tau $ and $\tau\vD \sigma$ , then $\sigma $ and $\tau $ are said to be tautologically equivalent (written $\sigma \te\tau$ ).

3. A Parsing Algorithm

The purpose of this section is to prove that we have used enough parentheses to eliminate any ambiguity in analyzing wffs. The existence of the extension $\bar v$ of a truth assignment $v$ will hinge on this lack of ambiguity.

这一部分是证明 $\bar v$ 的存在性的

$\textbf{LEMMA 13A}$

Every wff has the same number of left as right parentheses.

$\textbf{PROOF}$. The idea is that we start with sentence symbols (having zero left parentheses and zero right parentheses), and then apply formula-building operations which add parentheses only in matched pairs. We can rephrase this argument as follows: The set of “balanced” wffs (having equal numbers of left and right parentheses) contains all sentence symbols and is closed under the formula-building operations. The induction principle then assures us that all wffs are balanced.

$\textbf{LEMMA 13B}$

Any proper initial segment of a wff contains an excess of left parentheses. Thus no proper initial segment of a wff can itself be a wff.

We are now going to describe a procedure that, given an expression,

  • both will determine whether or not the expression is a legal wff,
  • and if it is, will construct the tree showing how it was built up from sentence symbols by application of the formula-building operations.
  • Moreover, we will see that this tree is uniquely determined by the wff.

4. Induction and Recursion

4.1. Induction

Induction is a special type of construction that occurs frequently both in logic and in other branches of mathematics.

We may want to construct a certain subset $C$ of a set $U$ by starting with some initial elements of $U$, and applying certain operations to them over and over again. The set we seek ($C$) will be the smallest set containing the initial elements and closed under the operations. Its members will be those elements of $U$ which can be built up from the initial elements by applying the operations some finite number of times.

In the special case of immediate interest to us, $U$ is the set of expressions, the initial elements are the sentence symbols, and the operations are $\mathcal E_{\neg}$, $\mE_{\land}$, etc. The set to be constructed is the set of wffs. But we will encounter other special cases later, and it will be helpful to view the situation abstractly here. To simplify our discussion, we will consider an initial set $B \subseteq U$ and a class $\mathcal F$ of functions containing just two members $f$ and $g$, where

$$ f : U \times U \to U\ \text{ and }\ g : U → U $$

Actually $\mathcal F$ need not be finite.

In defining the target subset $C$ more formally, we have our choice of two definitions.

  1. We can define it “from the top down” as follows:

    1. $def: \textbf{Closed}$

      Say that a subset $S$ of $U$ is closed under $f$ and $g$ iff whenever elements $x$ and $y$ belong to $S$, then so also do $f(x, y)$ and $g(x)$.

    2. $def: \textbf{Inductive}$

      Say that $S$ is inductive iff $B \subseteq S$ and $S$ is closed under $f$ and $g$.

      Let $C^*$ be the intersection of all the inductive subsets of $U$ ; thus $x ∈ C^*$ iff $x$ belongs to every inductive subset of $U$. It is not hard to see that $C^*$ is itself inductive. Furthermore, $C^*$ is the smallest such set, being included in all the other inductive sets.

  2. The second (and equivalent) definition works “from the bottom up.”

    We want $C_*$ to contain the things that can be reached from $B$ by applying $f$ and $g$ a finite number of times. Temporarily define a construction sequence to be a finite sequence $〈x_1, . . . , x_n〉$ of elements of $U$ such that for each $i ≤ n$ we have at least one of

    $$\begin{array}{lll}x_{i} \in B & & \\ x_{i}=f\left(x_{j}, x_{k}\right) & \text { for some } & j<i, k<i \\ x_{i}=g\left(x_{j}\right) & \text { for some } & j<i\end{array} $$

    Then let $C_*$ be the set of all points $x$ such that some construction sequence ends with $x$. Let $C_n$ be the set of points $x$ such that some construction sequence of length $n$ ends with $x$. Then $C_1 = B$ and $\displaystyle C_* = \bigcup_n C_n$, where:

$$C_{1} \subseteq C_{2} \subseteq C_{3} \subseteq \cdots $$

At this point we should verify that our two definitions are actually equivalent, i.e., that $C^* = C_*$ .

  • $C^{*}\ {\subseteq}\ C_*$ : 由于 $C^*$ 是 $U$ 最小的归纳子集, 所以只要能证明到 $C_*$ is inductive.
  • $C_{*}\ {\subseteq}\ C^*$ :

4.2. Recursion

5. Sentential Connectives

cont.