这一节讲的很迷幻, 哥们记完了笔记但还是不怎么懂
1. $\small \text{Symbol Table}$
$def$: 符号表 ($\text{Symbol Table}$) 是用于保存各种信息的数据结构.

$\text{DSL}$ (领域特定语言): 通常只有单作用域 (全局作用域), e.g. $\text{SQL}$, $\text{MATLAB}$
$\text{GPL}$ (通用程序设计语言): 通常需要嵌套作用域, e.g. $\text{Python}$, $\text{Java}$
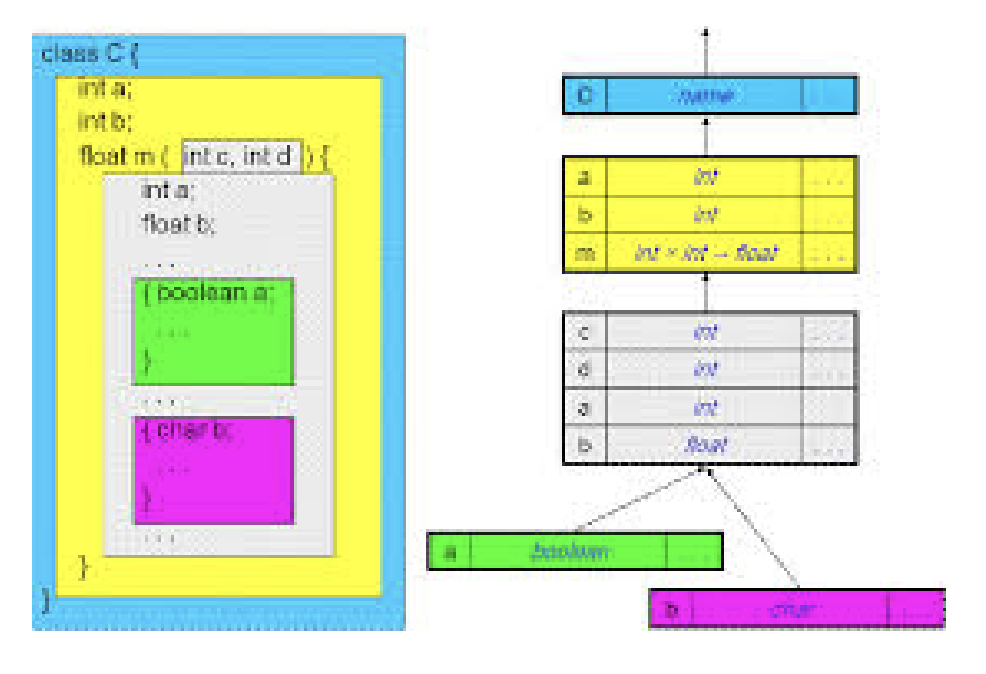
在 SysY 语言中, 我们结合 Symbol / Scope / Type 等抽象的概念开展了如下的设计.
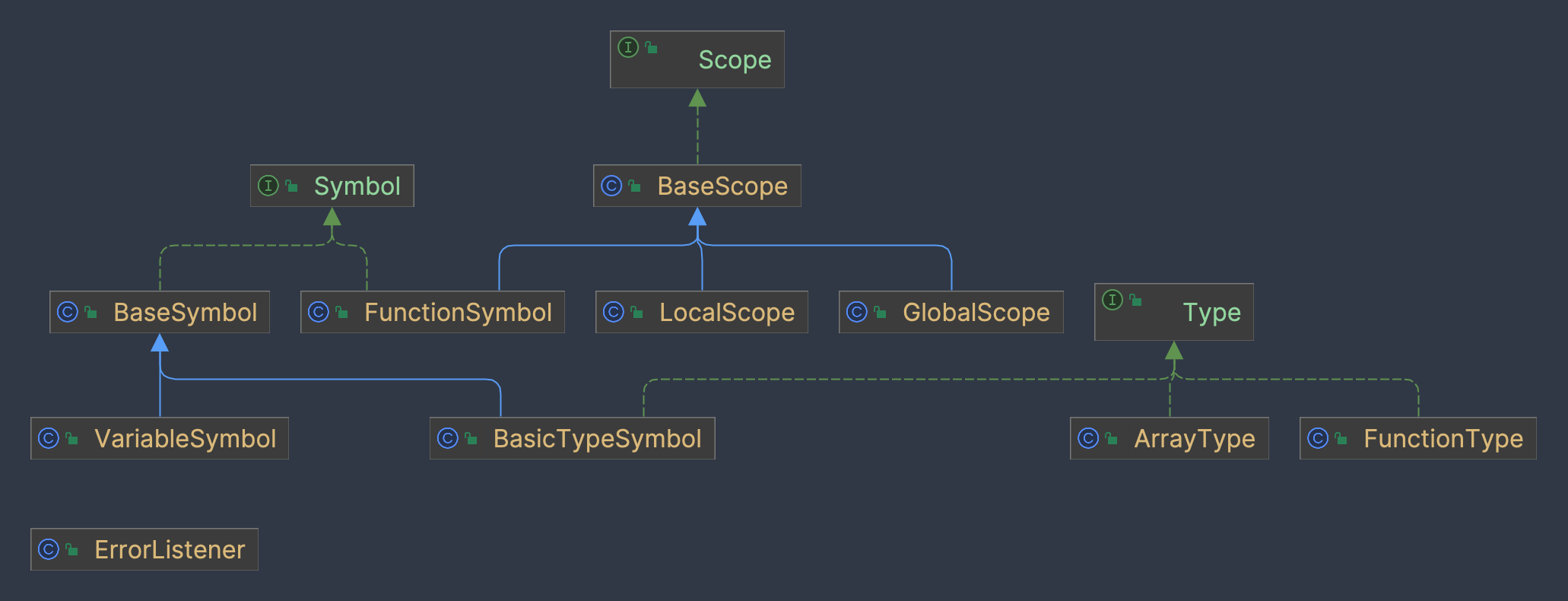
2. $\small\text{Attribute Grammar}$
对于已经涉及到的几个概念, 可以有对应的文法 $G$ 来刻画.
- Lexical Analysis: Regular Grammar
- Syntactic Analysis: Context-free Grammar
- Semantic Analysis: Attribute Grammar

$Knuth$ 在他的论文中提到了两种属性:
- $\text{synthesized attributes}$
- $\text{inherited attributes}$
针对这两种属性, 一般地, 有两种计算属性值的方法:
- Offline: 已经有了语法分析树, 按照从左到右的深度优先顺序遍历语法分析树, 计算属性值. 关键: 在合适的时机执行合适的动作,计算相应的属性值
- Online: 在语法分析过程中实现属性文法. 基本思想: 一个动作在它左边的所有文法符号都处理过之后立刻执行.$B\to X\{a\}Y$ (其中 $\{a\}$ 表示 action)
在这里, 我们主要考虑 Online 方法
2.1. $\small\text{Syntax-Directed Definition}$
$def:$ 语法制导($\text{SDD}$) 是一个 上下文无关文法 和 属性 及 规则 的结合. $\text{SDD}$ 唯一确定了语法分析树上每个 非终结符节点的属性值.

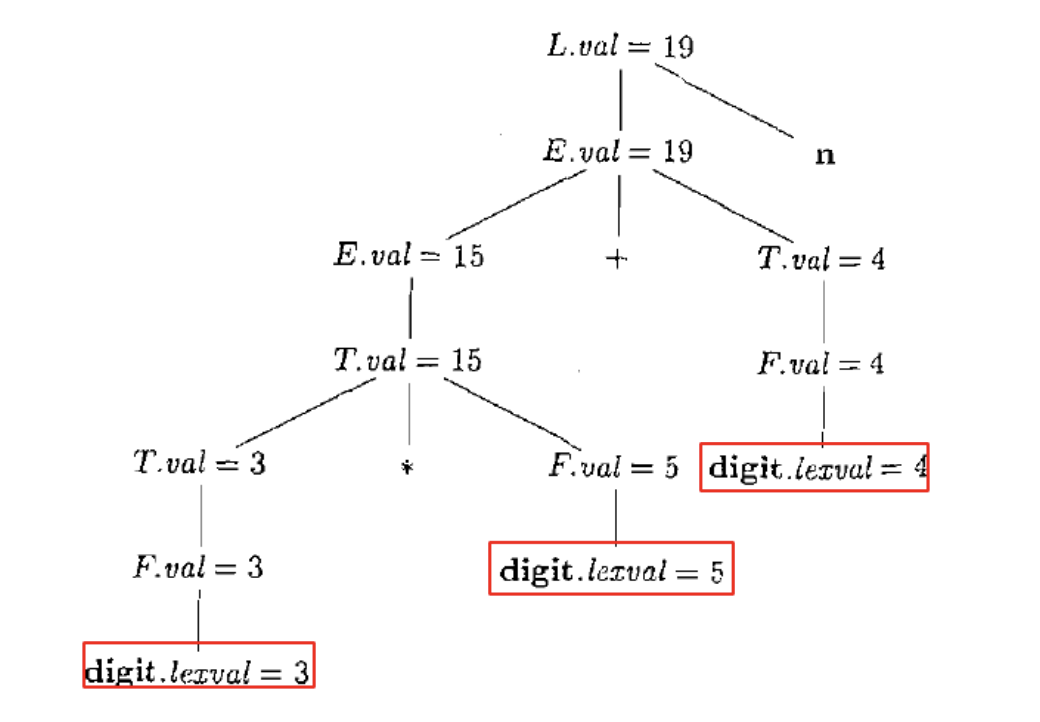
与 $\text{SDD}$ 相对应的, 我们可以将语法树扩充为注释 (annotated) 语法分析树: 显示了各个属性值的语法分析树. e.g.
2.2. $\small\text{Synthesized Attribute}$
$def:$ 节点 $N$ 上的综合属性只能通过 $N$ 的子节点或 $N$ 本身的属性来定义.

2.3. $\small{S \text{-Attributed Definition}}$
$def:$ 特别地, 如果一个 $\text{SDD}$ 的每个属性都是综合属性, 则它是 $S$ 属性定义.
为了描述 $S$ 属性定义, 我们借助一个叫做依赖图的新概念. 依赖图用于确定一棵给定的语法分析树中各个属性实例之间的依赖关系. 下图是依赖图的一个例子.
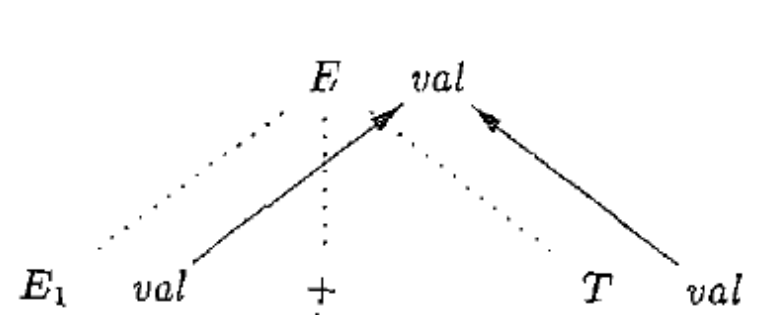
更加具体地, $S$ 属性定义的依赖图刻画了属性实例之间自底向上的信息流动. $S$ 属性定义的一个依赖图如下.
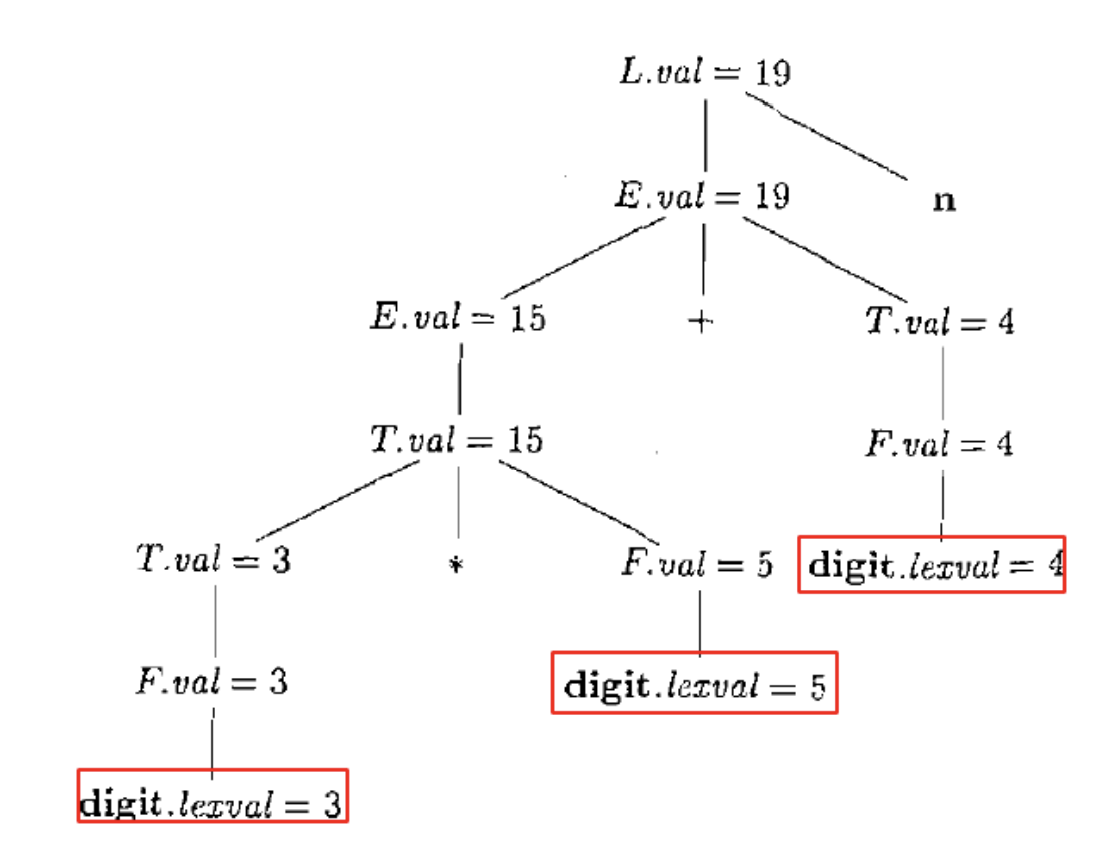
此类属性值的计算可以在自顶向下的 $LL$ Syntactic Analysis过程中实现: 在 $LL$ 语法分析器中, 递归下降函数 $A$ 返回时, 计算相应节点 $A$ 的综合属性值.
2.4. $\small\text{Inherited Attribute}$
节点 $N$ 上的继承属性只能通过 $N$ 的父节点、$N$ 本身和 $N$ 的兄弟节点 (可以是左兄弟或者是右兄弟) 上的属性来定义.

信息流向: 先从左向右、从上到下传递信息, 再从下到上传递信息. 同样, 可以通过依赖图来可视化这样的信息传递流向.
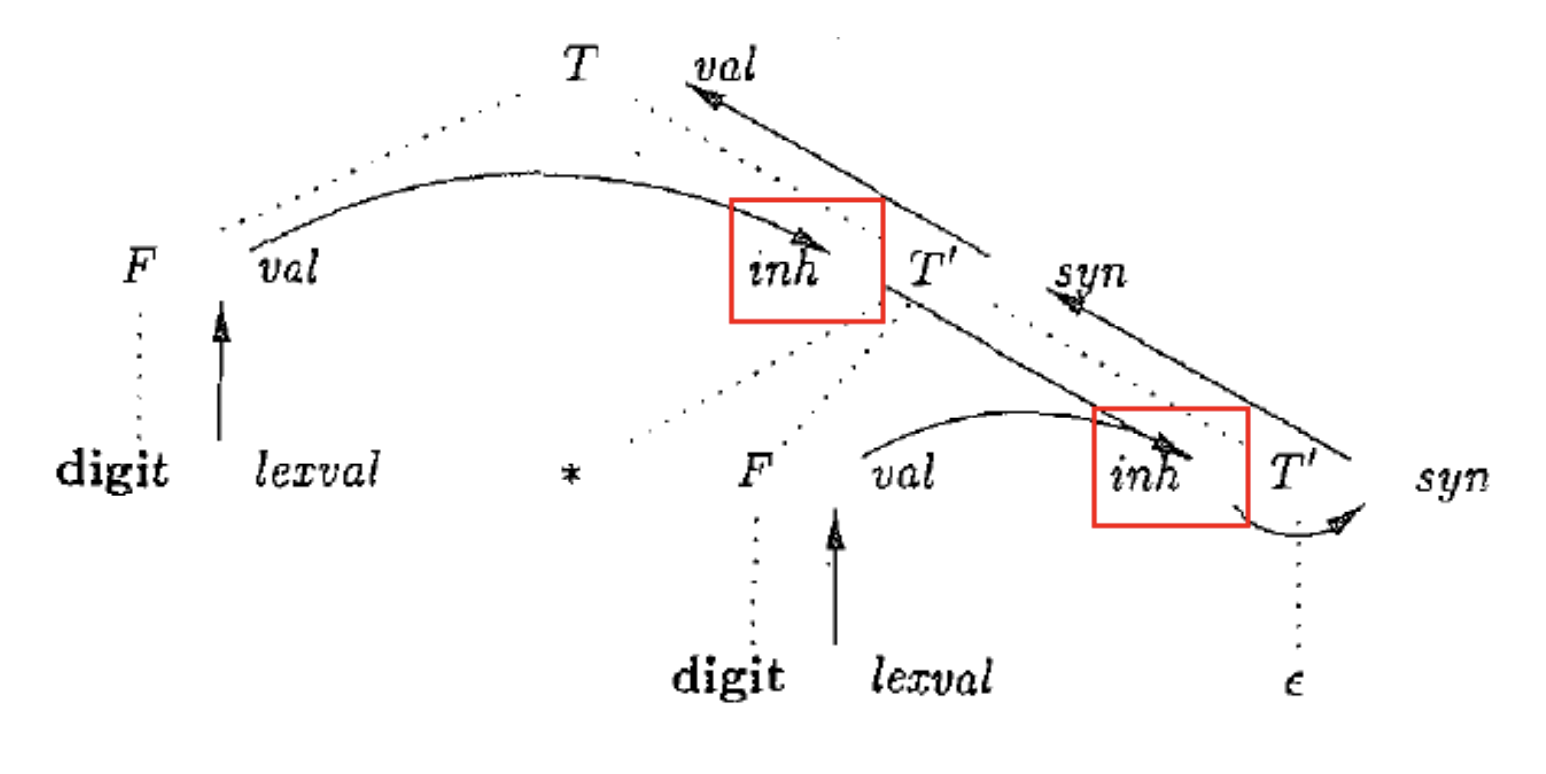
2.5. $\small{L\text{-Attributed Definition}}$
$def$: 如果一个 $\text{SDD}$ 的每个属性都满足如下的条件, 则它是 $L$ 属性定义.
$(1)$ 要么是综合属性
$(2)$ 要么是继承属性, 但是它的规则满足这样的限制: 对于产生式 $A \to X_1X_2 ...X_n$ 及其对应规则定义的继承属性 $X_i .a$, 这个规则只能使用:
($\text{a}$) 和**产生式头 $A$** 关联的继承属性.
($\text{b}$) 位于**$X_i$ 左边的文法符号实例 $X_1, X_2, ..., X_{i−1}$ 相关的继承属性或综合属性**.
($\text{c}$) 与这个 $X_i$ 的实例本身相关的继承属性或综合属性, 但是在由这个 $X_i$ 的全部属性组成的依赖图中不存在环.
一个自然的想法是, 将 $L$ 属性定义和 $LL$ 文法结合起来 (毕竟 Online 模式的属性定义就是要在文法分析的时候加进来)
对于递归下降的子过程 $A \to X_1...Xi...X_n$
- 在调用 $X_i$ 子过程之前, 计算 $X_i$ 的继承属性
- 以 $X_i$ 的继承属性为参数调用 $X_i$ 子过程
- 在 $X_i$ 子过程返回之前, 计算 $X_i$ 的综合属性
- 在 $X_i$ 子过程结束时返回 $X_i$ 的综合属性
$\small{\text{S-AD} \ \ V.S.\ \ \text{L-AD}}$
对于表达式 $XY^*$ 我们分别给出 (左递归的) $S$ 属性定义和 (右递归的) $L$ 属性定义如下:
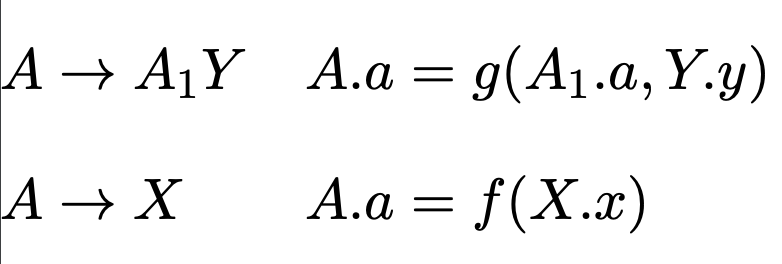



2.6. $\small\text{Postfix Notation}$
$def$: 后缀表示 ($\text{Postfix Notation}$) 的递归定义如下:
$(1)$ 如果 $E$ 是一个 变量或常量, 则 $E$ 的后缀表示是 $E$ 本身.
$(2)$ 如果 $E$ 是形如 $E_1\ op\ E_2$ 的表达式, 则 $E$ 的后缀表示是 $E^′_1E^′_2\ op$, 这里 $E^′_1$ 和 $E^′_2$ 分别是 $E_1$ 与 $E_2$ 的后缀表达式.
$(3)$ 如果 $E$ 是形如 $(E_1)$ 的表达式, 则 $E$ 的后缀表示是 $E_1$ 的后缀表示.

2.7. $\small\text{Syntax-Directed Translation Scheme}$
$def$: 语法制导的翻译方案 ($\text{SDT}$) 是在其产生式体中嵌入语义动作的上下文无关文法.

一个自然的想法是, 如何将带有语义规则的 $\text{SDD}$ 转换为带有语义动作的 $\text{SDT}$: 使用**后缀翻译方案**, $i.e.$ 所有动作都在产生式的最后.