Relational Data Theory

Refererences:

R. Ramakrishnan and J. Gehrke, Database Management Systems, 19.1-19.6

1. Relational Schema

$\textbf{Definition}$ formally, a relation schema $R$ can be defined as $R=(U, D, DOM, F)$, where

• $R:$ 关系名
• $U:$ 组成该关系的属性的集合
• $D:$ $U$ 中属性所来自的域
• $DOM:$ 属性向域的映象集合 (常常直接说明为属性的类型 & 长度)
• $F:$ 属性组 $U$ 上的一组数据依赖

也可以简记为 $R(U)$ 或 $R(A_1, A_2, ..., A_n)$, where $A_1, A_2, ..., A_n$ 为属性名称

由于$D$, $DOM$ 与模式设计关系不大, 因此可以把关系模式看作一个三元组

$$\text{Relational Schema }:=(R,U,F) $$

当且仅当 $U$ 上的一个关系 $r$ 满足 $F$ 时, $r$ 称为关系模式 $R$ 的一个关系.

作为二维表, 关系要符合一个最基本的条件: 每个分量必须是不可分开的数据项. 满足了这个条件的关系模式就属于第一范式 (1NF)

数据依赖: 是一个关系内部属性与属性之间的一种约束关系 (本质上是现实世界属性间相互联系的抽象).
主要类型

• 函数依赖 (Functional Dependency, 简记为$\textsf{FD}$)
• 多值依赖 (Multi-Valued Dependency, 简记为 $\textsf{MVD}$)

2. FD & Key

2.1. Functional Dependency

Definition of Functional Dependency: A functional dependency is a kind of integrity constraint that geralizes the concept of a key.

我们通过 FD 的概念来刻画属性之间的依赖关系.
注意函数依赖的对象是属性集合: 属性集合与属性集合之间产生函数依赖

Definition of Determinant

Suppose $R(U)$ is a relation schema over a set $U$ of attributes, and $X,Y\subset U$ are two sets of attributes. if there is a mapping $f:X\to Y$, then we say "$X$ functionally determines $Y$ " or “$Y$ functionally depends on $X$”, denoted by $X\to Y$. $X$ is then called the Determinant (决定因素) of this functional dependency.

Similarly,

• if $X\to Y$ and $Y\to X$, then we say $X$ and $Y$ are equivalent and denote this by $X\leftarrow \rightarrow Y$.

• if $Y$ is not functionally dependent on $X$, then we denote this by $X\not \to Y$.

• trivial FD: $X\to Y \land Y\subset X$

• non-trivial FD: $X\to Y\land Y\not \subset X$

Definition of Closure of a Set of Attributes

The set of all FDs implied by a given set $F$ of FDs is called the closure of $F$, denoted as $F^+$.

2.2. Armstrong’s Axioms

Definition of Armstrong’s Axioms: The following FD rules can be applied to all FDs:

• Reflexivity: If $Y\subset X$, then $X\to Y$
• Augmentation: If $X\to Y$, then forall $Z$, $XZ\to YZ$
• Transitivity: If $X\to Y$ and $Y\to Z$, then $X\to Z$

It can be proved that Axioms of Armstrong are:

• Sound: in that they generate only FDs in $F^+$ when applied to a set $F$ of FDs, and
• Complete: in that they generate all FDs in $F^+$.

It is convenient to use some additional rules while reasoning about $F^+$:

• Union: If $X\to Y$ and $X\to Z$, then $X\to YZ$.
• Decomposition: If $X\to YZ$, then $X\to Y$ and $X\to Z$.

$\textbf{Definition}$: Complete, Partial and Transitive Functional Dependency

也就是说,
候选键是不含有多余属性的超键
超键是在关系中能唯一标识元组的属性集 (显然, 超键可以很大, 甚至极端一点, 超键可以是上面的 $U$ )

主键是一种设计, 用户可以根据需要从任何一个候选键中选择一个作为主键

3. Normal Forms and Decomposition

3.1. Several Types of Functional Dependencies

在 $R(U)$ 中,

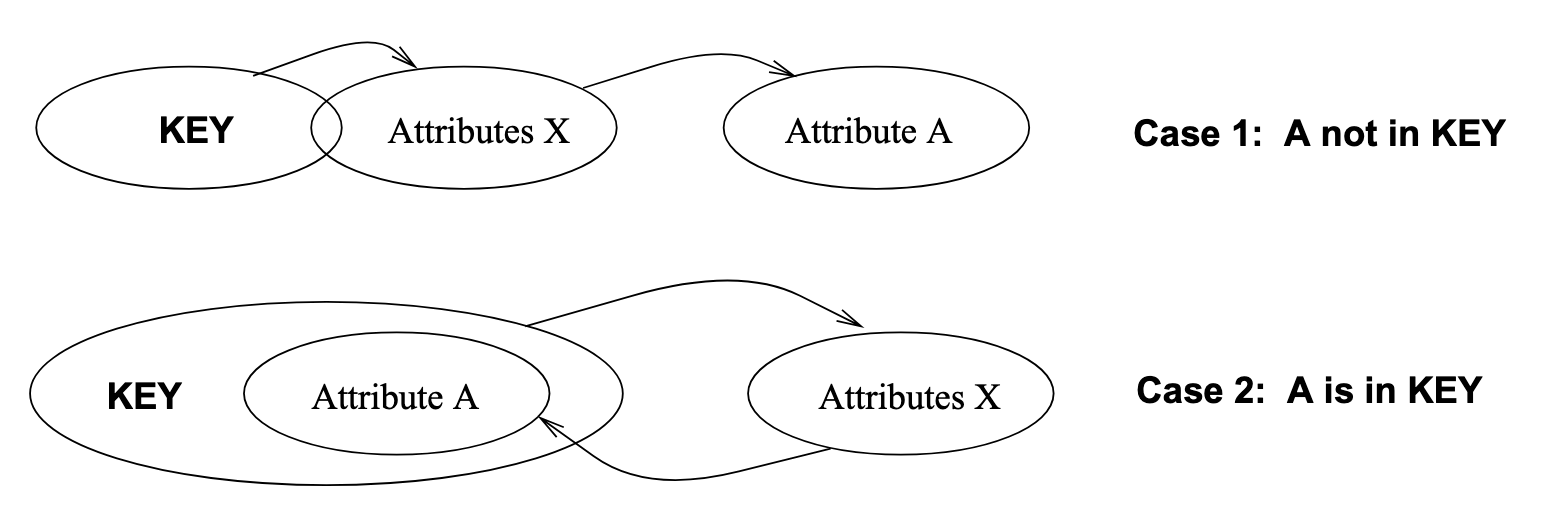
• 如果 $X\to Y$, 并且对于 $X$ 的任何一个真子集 $X^\prime$, 都有 $X^\prime\not \to Y$, 则称 $Y$ 对 $X$ 完全函数依赖. 记作 $X \stackrel F{\to} Y$

• 如果 $X\to Y$, 但是 $Y$ 不完全函数依赖于 $X$, 则称 $Y$ 对 $X$ 部分函数依赖, 记作 $X\stackrel P \to Y$

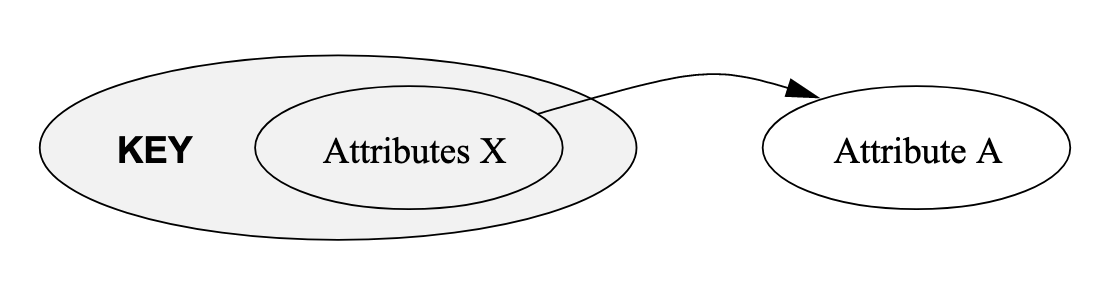
• 如果 $Y\to Z$, 且 $Y \not \subset X$, 且 $Y \not \to X$, 但是 $X \stackrel F{\to} Y$, 则称 $Y$ 对 $X$ 传递函数依赖, 记作 $X\stackrel T \to Y$

用非形式化的语言解释, 就是说:

• 如果 $X$ 能决定 $Y$ , 并且 $X$ 再少一点属性都不能决定 $Y$ , 那么称 $X \stackrel F{\to} Y$
• 如果 $X$ 能决定 $Y$ , 并且 $X$ 的某一组子属性就可以决定 $Y$ , 那么称 $X \stackrel P{\to} Y$
• 如果 $X$ 能决定 $Y$ , 并且 $Y$ 能决定 $Z$, 但是 $Y$ 不能决定 $X$, 那么称 $X \stackrel T{\to} Y$ (说明传递依赖是比较弱的关系, 如果 $Y$ 和 $X$ 能相互决定的话, $X$ 和 $Y$ 在形式上是等价关系, $Z$ 将直接由 $X$ 决定)

3.2. Normal Forms

Given a relation schema, we need to decide whether it is a good design or we need to decompose it into smaller relations. To provide such guidance, several normal forms have been proposed.

也就是说, 给定一个关系模式, 我们只需要知道它恰好符合哪一种范式, 从而可以知道它是否是一个好的设计, 或者我们需要将其分解为更小的关系.

这篇文章对范式给出了非常好的介绍

根据严苛程度, 可以将范式分为:

• $\text{1NF}:$ 关系中的每个属性都不可再分
• $\text{2NF}:$ 在 $1\text{NF}$的基础之上, 消除了non-primary attributes 对于 candidate keys 的 部分函数依赖 (i.e. 每个非主键列都完全依赖于主键, 而不是依赖于部分主键)
• $\text{3NF}:$ 在 $2\text{NF}$ 的基础之上, 消除了non-primary attributes 对于 candidate keys 的 传递函数依赖 (i.e. 消除传递依赖)
• $\text{BCNF}:$ 在 $3\text{NF}$ 的基础上消除 primary attributes 对于键的 partial and transitive functional dependencies
• $\text{4NF}$
• $\text{5NF}$

where: $5\text{NF} \subset 4\text{NF} \subset \text{BCNF} \subset \text{3NF} \subset \text{2NF} \subset \text{1NF}$

这里要注意.

1. $2\text{NF}$: 既然是数据库, 那么一切 non-primary attributes 都是依赖于每一个 candidate key 的. 我们只是希望数据不冗余, 所以我们要求每个 non-primary attributes 不能 partial dependent 于 candidate key.
2. 一般来说 $1\text{NF}$ 和 $2\text{NF}$ 在数据库设计中都是可以忽略的. 我们主要的工作是确保数据库的设计符合 $3\text{NF}$. 到 $\text{BCNF}$ 和 $4\text{NF}$ 的时候就变成一个 tradeoff 问题了
3. $R$ satisfies $3\text{NF}$ iff every non-trivial FD $X\to Y$ of $R$ saitisfies either “$X$ is a superkey” or “$Y$ is part of a candidate key”.
4. $R$ satisfies $\text{BCNF}$ iff every non-trivial FD $X\to Y$ of $R$ saitisfies “$X$ is a superkey”.

4. Decomposition

某一关系模式$R$ 为第 $n$ 范式, 可简记为 $R\in n\text{NF}$. 一个低一级范式的关系模式, 通过模式分解 (schema decomposition) 可以转换为若干个高一级范式的关系模式的集合, 这种过程就叫规范化 (normalization).

A decomposition should preserve two important properties:

• Lossless Join: 通过连接操作, 可以恢复原来的关系
• Dependency Preservation: 保持原来的函数依赖

4.1. Lossless Join Decomposition

Definition of Lessless-join Decomposition.
A decomposition of $R$ into two schemas with attribute sets $X$ and $Y$ is said to be a lossless-join decomposition with respect to $F$ if, for every instance $r$ of $R$ that satisfies the dependencies in $F$, $\pi_X(r)\Join \pi_Y (r) = r$.

Note that $r\subset\pi_X(r)\Join \pi_Y (r)$ always holds, but the reverse may not be true. The condition $r=\pi_X(r)\Join \pi_Y (r)$ is called lossless join.
All decompositions used to eliminate redundancy must be lossless. The following simple test is very useful

Theorem Let $R$ be a relation and $F$ be a set of FDs that hold over $R$. The decomposition of $R$ into relations with attribute sets $R_1$ and $R_2$ is lossless if and only if $F^+$ contains either the FD $R_1 \cap R_2 \to R_1$ or the FD $R_1 \cap R_2 \to R_2$.

4.2. Dependency Preservation Decomposition

Definition of Dependency Preservation Decomposition.
The decomposition of relation schema $R$ with FDs $F$ into schemas with attribute sets $X$ and $Y$ is dependency-preserving if $(F_X ∪ F_Y )^+ = F^+$.

Decomposition Algorithm

Algorithm of Decomposition into BCNF

1. Start with the original relation $R$ and the set of FDs $F$.
2. Check if $R$ is in BCNF. If so, stop.
3. If not, find a FD $X\to Y$ that violates BCNF.
4. Decompose $R$ into $R_1(XY)$ and $R_2(XZ)$, where $Z=R-Y$.
5. Repeat the process for $R_1$ and $R_2$.

Note that it is always possible to decompose a relation into BCNF and that the decomposition is lossless, but it may not be dependency preserving.

Algorithm of Decomposition into 3NF

// TODO

Note that it is always possible to decompose a relation into BCNF and that the decomposition is lossless and dependency preserving.