Query Performance

CS › DBMS

We have alternative ways of evaluating a given query

  • Equivalent Expressions
  • Different Algorithms for Each Operation

1. Query Performance

Consider such a query:

1
2
3
SELECT i.name, C.title
FROM instructors i, teaches t, courses c
WHERE i.dept_name = 'Music' AND i.ID = t.courseID AND t.courseID = c.courseID;

An Evaluation Plan defines exactly what algorithm is used for each operation, and how the execution of the operations is coordinated. For example we can parse the query into such a query tree:

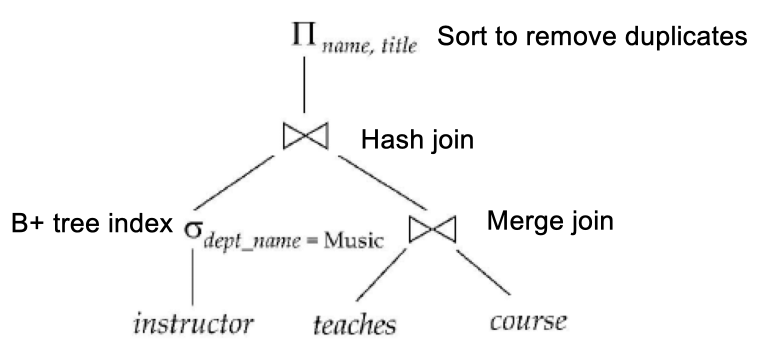
Cost difference between evaluation plans for a query can be enormous (e.g. seconds vs. days in some cases)

Cost-based query optimization includes the following steps:

  1. Generate logically equivalent expressions using equivalence rules.
  2. Annotate resultant expressions to get alternative query plans.
  3. Choose the cheapest plan based on estimated cost.

Estimation of plan cost based on:

  1. Statistical information about relations. Examples: number of tuples, number of distinct values for an attribute.
  2. Statistics estimation for intermediate results to compute cost of complex expressions.
  3. Cost formulae for algorithms, computed using statistics.

Some Equivalence Rules:

  • Conjunctive selection operations can be deconstructed into a sequence of individual selections.
$$\sigma_{\theta_1 \wedge \theta_2}(R) = \sigma_{\theta_1}(\sigma_{\theta_2}(R)) $$
  • Selection operations are commutative.
$$\sigma_{\theta_1 \wedge \theta_2}(R) = \sigma_{\theta_2 \wedge \theta_1}(R) $$
  • Only the last in a sequence of projection operations is needed, the others can be omitted.
$$\pi_{A_1}(\pi_{A_2}(R)) = \pi_{A_1}(R) $$
  • Selections can be combined with Cartesian products and theta joins.
$$\begin{aligned} \sigma_{\theta_1}(R \times S) &= R\Join_{\theta_1}S \\ \sigma_{\theta_1}(R \Join_{\theta_2} S) &= R \Join_{\theta_2 \wedge \theta_1} S \end{aligned} $$
  • Theta-join operations (and natural joins) are commutative.
$$R \Join_{\theta} S = S \Join_{\theta} R $$
  • Natural join operations are associative:
$$R \Join S \Join T = R \Join (S \Join T) $$
  • Theta-join operations are equivalent in the following manner:
$$(R \Join_{\theta_1} S) \Join_{\theta_2} T = R \Join_{\theta_1 \wedge \theta_2} (S \Join T) $$

  • The selection operation distributes over the theta join operation under the following two conditions:

    • When all the attributes in $\theta_0$ involve only the attributes of R being joined.
    $$\sigma_{\theta_0}(R \Join_{\theta} S) = \sigma_{\theta_0}(R) \Join_{\theta} S $$
    • When $θ_1$ involves only the attributes of R and $θ_2$ involves only the attributes of S.
    $$\sigma_{\theta_1}(R) \Join_{\theta} \sigma_{\theta_2}(S) = \sigma_{\theta_1 \wedge \theta_2}(R \Join S) $$

  • The projection operation distributes over the theta join operation as follows:

    • If $\theta$ involves only the attributes from $L_1\cup L_2$
    $$\pi_{L_1\cup L_2}(R \Join_{\theta} S) = \pi_{L_1}(R) \Join_{\theta} \pi_{L_2}(S) $$