Probabilistic Learning

1. Concepts

1.1. Concavity

对于一元函数, 有定义如下

function $f$ is convex $\iff$

$$\forall x_{1}, x_{2} \in \mathrm{dom}, \forall t \in[0,1]:\quad f\left(t x_{1}+(1-t) x_{2}\right) \geq t f\left(x_{1}\right)+(1-t) f\left(x_{2}\right)$$

function $f$ is concave $\iff$

$$\forall x_{1}, x_{2} \in \mathrm{dom}, \forall t \in[0,1]: \quad f\left(t x_{1}+(1-t) x_{2}\right) < t f\left(x_{1}\right)+(1-t) f\left(x_{2}\right)$$

从导数的角度考虑, 对于 $x\in \mathbb R$:

$$\mathrm{function\ } f \mathrm{\ is\ convex} \iff\frac{\mathrm d^2 f}{\mathrm dx^2}\geq 0$$

对于多元函数, $\boldsymbol x\in\mathbb R^d$:

$$\mathrm{function\ } f \mathrm{\ is\ convex} \iff\nabla^{2} f(\boldsymbol x) \succeq 0$$

其中 $\nabla^2f$ 指的是 $f$ 的 $\text{Hessian}$ 矩阵

1.2. $\text{Jensen}$ Inequality

relatively trivial, see wikipedia for more details

1.3. Normal Distribution

详情查看我的这篇数据科学笔记

2. KNN

$k$ - Nearest Neighbor Classifier (KNN)

2.1. Steps

• 计算测试样本 $\boldsymbol {\bar x}$ 和 $D_{train}$ 中所有训练样本 $\boldsymbol {x_i}$ 之间的距离 $d(\bar {\boldsymbol x}, { \boldsymbol x_i})$

• 对所有距离值 (相似度值) 进行升序 (降序) 排列

• 选择化个最近 (距离最小/相似度最大) 的训练样本

• 采用投票法, 将近邻中样本数最多的类别标签分配给无

k 的取值变化有很多影响:

• $k$ 一般取奇数值, 避免平局
• $k$ 取不同的值, 分类结果可能不同
• $k$ 值较小时, 对噪声敏感, 整体模型变得复杂, 容易过拟合
• $k$ 值较大时, 对噪声不敏感, 整体模型变得简单, 容易欠拟合

2.2. 1-NN

$$\begin{aligned} P(\text { err }) & \simeq 1-\sum_{c \in \mathcal{Y}} P^{2}(c \mid \boldsymbol{x}) \\ & \leq 1-P^{2}\left(c^{*} \mid \boldsymbol{x}\right) \\ & =\left(1+P\left(c^{*} \mid \boldsymbol{x}\right)\right)\left(1-P\left(c^{*} \mid \boldsymbol{x}\right)\right) \\ & \leq 2 \times\left(1-P\left(c^{*} \mid \boldsymbol{x}\right)\right) \end{aligned}$$

3. GMM

3.1. Mixture Model

在统计学中, 混合模型 (Mixture model) 是用于表示母体中子母体的存在的几率模型, 换句话说, 混合模型表示了测量结果在母体中的几率分布, 它是一个由数个子母体之几率分布组成的混合分布. 混合模型不要求测量结果供关于各个子母体之几率分布的资讯即可计算测量结果在母体分布中的几率.

举一个不是那么严谨的例子(Wikipedia), 若是我们手上有一个班级中所有学生某一次考试的各项科目分数分布, 并且每一科的分数都大致依照高斯分布. 则当我们要描述每个学生的总分分布时, 单高斯模型及多维的高斯模型不一定能很好的描述这个分布, 因为每一科的分布的情形都不尽相同, 此时我们可以用高斯混合模型更好的来描述这个问题.

3.2. $\text{Gaussian}$ Mixture Model

高斯混合模型可以看作是由若干个 ($n$) 单高斯模型组合而成的模型, 这 $n$ 个子模型是混合模型的隐变量 (Hidden variable). 一般来说, 一个混合模型可以使用任何概率分布, 这里使用高斯混合模型是因为高斯分布具备很好的数学性质以及良好的计算性能.

形式化地, GMM 的 PDF 有定义如下

$$\begin{aligned} p(x) & =\sum_{i=1}^{N} \alpha_{i} N\left(\boldsymbol{x} ; \boldsymbol{\mu}_{i}, \Sigma_{i}\right) \\ & =\sum_{i=1}^{N} \frac{\alpha_{i}}{(2 \pi)^{d / 2}\left|\Sigma_{i}\right|^{1 / 2}} \cdot\exp \left(-\frac{1}{2}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)^{\mathsf T} \Sigma_{i}^{-1}\left(\boldsymbol{x}-\boldsymbol{\mu}_{i}\right)\right)\end{aligned}$$

其中:

• 随机变量 $\boldsymbol X\in \mathbb R^d$
• $N$ 表示该 GMM 有 $N$ 个单变量 $\text{Gaussian}$ 分布
• $\forall i:\alpha_i>0,\displaystyle\sum_{i=1}^N\alpha_i=1$
• 参数 $\boldsymbol \theta=\left\{\alpha_i,\boldsymbol \mu_i,\Sigma_i\right\}_{i=1}^{N}$

显然从 GMM 中采出样本 $x$ 需要两步:

• 先从 $Z$ 中采样得到 $i$: 假设随机变量 $Z\in \{1,2,\ldots,N\}$ 符合离散分布, 也就是 $p(Z=i)=\alpha_i$
• 再从第 $i$ 个 $\text{Gaussian}$ 分布 $\mathbb N(\mu_i, \sigma_i)$中采样 $x$

4. MLE

详情查看我的这篇数据科学笔记

5. EM Algorithm

5.1. Principle

Expectation-Maximization algorithm

EM 算法是一个迭代的算法, 采用极大似然估计 MLE 对统计模型中的参数进行估计. 特别是针对含有无法观测的隐变量的模型.

通常, 引入隐变量之后会有两个参数, EM 算法会先固定其中的一个参数, 然后使用 MLE 计算第二个变量值; 接着通过固定第二个变量, 在用 MLE 估计第一个变量值. 依次迭代, 直到收敛到局部最优解.

假设隐变量 $Z$ 的分布 $Q(Z\mid\theta)$ 是一个任意的离散分布, 满足:

$$\sum_{Z} Q(z \mid \theta)=1, Q(z \mid \theta) \geq 0$$

$$\begin{align*} \ell(\theta)=\ln \mathcal{L}(\theta \mid X) & =\sum_{X} \ln \sum_{Z} p(X, Z \mid \theta) \\ & =\sum_{X} \ln \sum_{Z} Q(Z \mid \theta) \frac{p(X, Z \mid \theta)}{Q(Z \mid \theta)} \tag{1}\\ & =\sum_{X} \ln E_{Q}\left[\frac{p(X, Z \mid \theta)}{Q(Z \mid \theta)}\right]\tag{2}\\ & \geq \sum_{X} E_{Q}\left[\ln \frac{p(X, Z \mid \theta)}{Q(Z \mid \theta)}\right] \tag{3}\\ & =\sum_{X} \sum_{Z} Q(Z \mid \theta) \ln \frac{p(X, Z \mid \theta)}{Q(Z \mid \theta)} \tag{4} \end{align*}$$

其中, $(2)\to(3)$ 显然是利用了 $\text{Jensen}$ 不等式. 要使得不等式取等, 必须有

$$\frac{p(X, Z \mid \theta)}{Q(Z \mid \theta)}=c$$

也就是说,

$$\begin{aligned} Q(Z \mid \theta) & =\frac{p(X, Z \mid \theta)}{c}=\frac{p(X, Z \mid \theta)}{c \cdot \sum_{Z} Q(Z \mid \theta)} \left(\longrightarrow \sum_{Z} Q(z \mid \theta)=1\right) \\ & =\frac{p(X, Z \mid \theta)}{\sum_{Z} c \cdot Q(Z \mid \theta)}=\frac{p(X, Z \mid \theta)}{\sum_{Z} p(X, Z \mid \theta)} \left(\longrightarrow \frac{p(X, Z \mid \theta)}{Q(Z \mid \theta)}=c \right)\\ & =\frac{p(X, Z \mid \theta)}{p(X \mid \theta)}=p(Z \mid X, \theta) \end{aligned}$$

此时固定 $\theta$, 计算 $Q(Z\mid \theta)=p(Z,x\mid \theta)$, 就可以得到 $\ell(\theta)$ 的下界. 然后继续优化这个下界:

$$\begin{aligned} \theta^{*} & =\underset{\theta \in \Theta}{\operatorname{argmax}} \ell(\theta) \\ & =\underset{\theta \in \Theta}{\operatorname{argmax}} \sum_{X} \sum_{Z} p(Z \mid X, \theta) \ln \frac{p(X, Z \mid \theta)}{p(Z \mid X, \theta)}\end{aligned}$$

5.2. Steps

形式化地, EM 算法可以写成如下的三步骤.

• $\textbf{E-Step}$: 利用可观测数据 $X$ 和当前的参数估计 $\hat{\boldsymbol \theta}^{(t)}$, 估计更好的隐藏变量 $Z$

$$Q^{t}=p\left(Z \mid X, \theta^{t}\right)=\frac{p\left(X, Z \mid \theta^{t}\right)}{\sum_{Z} p\left(X, Z \mid \theta^{t}\right)}$$

$$\gamma_{i j}=\mathbb{E}\left[z_{i j} \mid \boldsymbol{x}_{j}, \boldsymbol{\theta}^{(t)}\right]=\frac{\left.\alpha_{i}^{(t)} N\left(\boldsymbol{x}_{j} ; \boldsymbol{\mu}_{i}^{(t)}, \Sigma_{i}^{(t)}\right)\right)}{\sum_{k=1}^{N} \alpha_{k}^{(t)} N\left(\boldsymbol{x}_{j} ; \boldsymbol{\mu}_{k}^{(t)}, \Sigma_{k}^{(t)}\right)}$$

其中

• $1\le i\le N,1\le j\le M$
• $z_{ij}\in \{0,1\}$
• $z_{ij}=1\iff x_j$ 由第 $i$ 个 $\text{Gaussian}$ 分布产生

• $\textbf{M-Step}$: 利用可观测数据 $X$ 和当前的参数估计 $Z$, 估计更好的隐藏变量 变量 $\hat{\boldsymbol \theta}^{(t+1)}$

$$\boldsymbol{\theta}^{(t+1)}=\underset{\theta \in \Theta}{\operatorname{argmax}} \sum_{X} \sum_{Z} Q^{t} \ln \frac{p(X, Z \mid \theta)}{Q^{t}}$$

$$\begin{align} m_{i} &=\sum_{j=1}^{M} \gamma_{i j}, \\ \boldsymbol{\mu}_{i}^{(t+1)}&=\frac{1}{m_i}\sum_{j=1}^{M} \gamma_{i j} \boldsymbol{x}_{j}, \\ \Sigma_{i}^{(t+1)}&= \frac{1}{m_i}\sum_{j=1}^{M} \gamma_{i j}\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}^{(t+1)}\right)\left(\boldsymbol{x}_{j}-\boldsymbol{\mu}_{i}^{(t+1)}\right)^{\mathsf T} \\ \alpha_{i}&=\frac{1}{M}\sum_{j=1}^{M} \gamma_{i j}=\frac{m_{i}}{M} \end{align}$$

• $\textbf{Repeat}$: 重复上述两个步骤, 直到收敛.

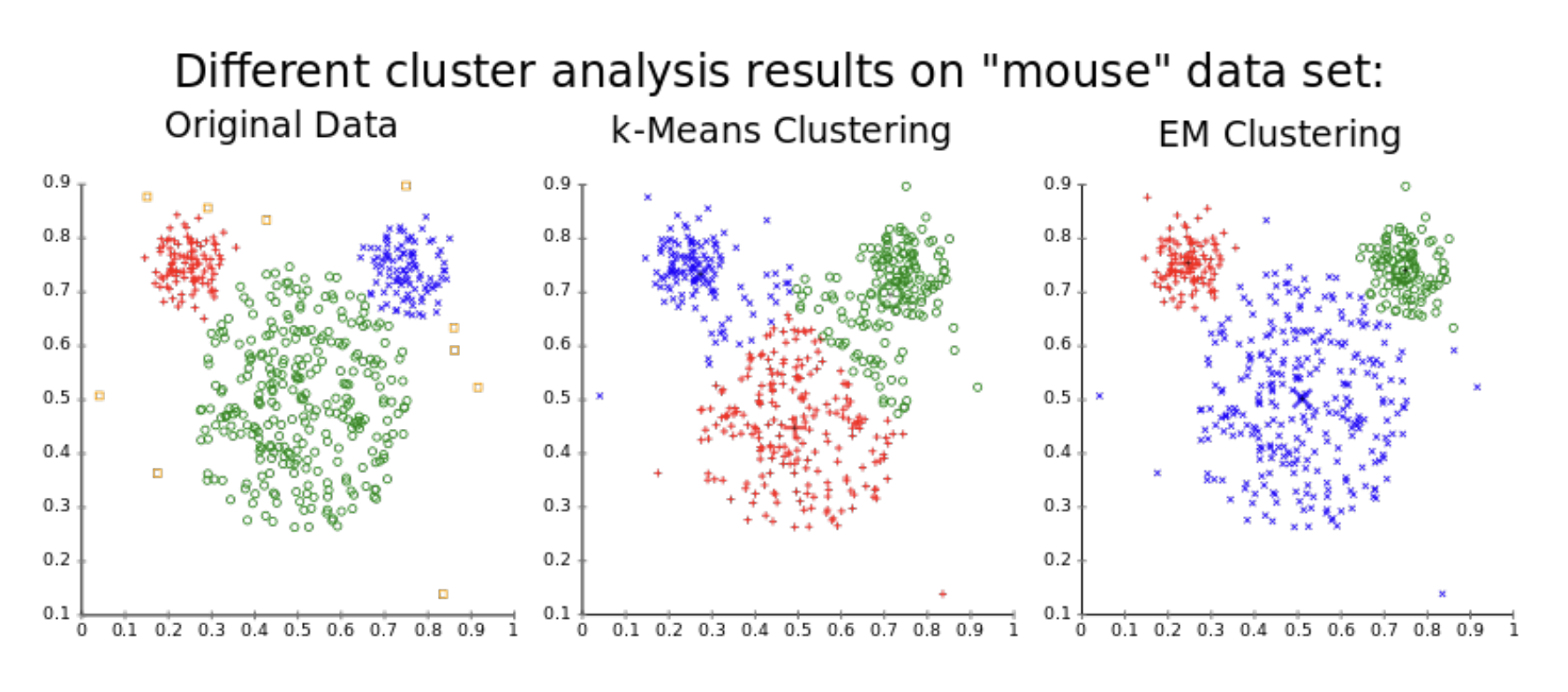
5.3. EM in K-means

K-means 算法本质上也使用了 EM 算法的设计.

对于聚类准则函数 $\displaystyle J=\sum_{j=1}^{c} \sum_{x \in S_{j}}\left\|x-m_{j}\right\|^{2}$

• 样本 $x_j$ 是可观测变量 $X$
• 类别标签 (簇) $S_j$ 看作是隐藏变量 $Z$
• 簇中心 / 聚类均值 $m_j$ 看作是参数 $\theta$
• 聚类准则函数 $J$ 看作是 $\theta$ 的似然函数