Neuron and Perceptron

CS › Machine Learning

1. Brain and Neurons

1.1. Biomimetic design

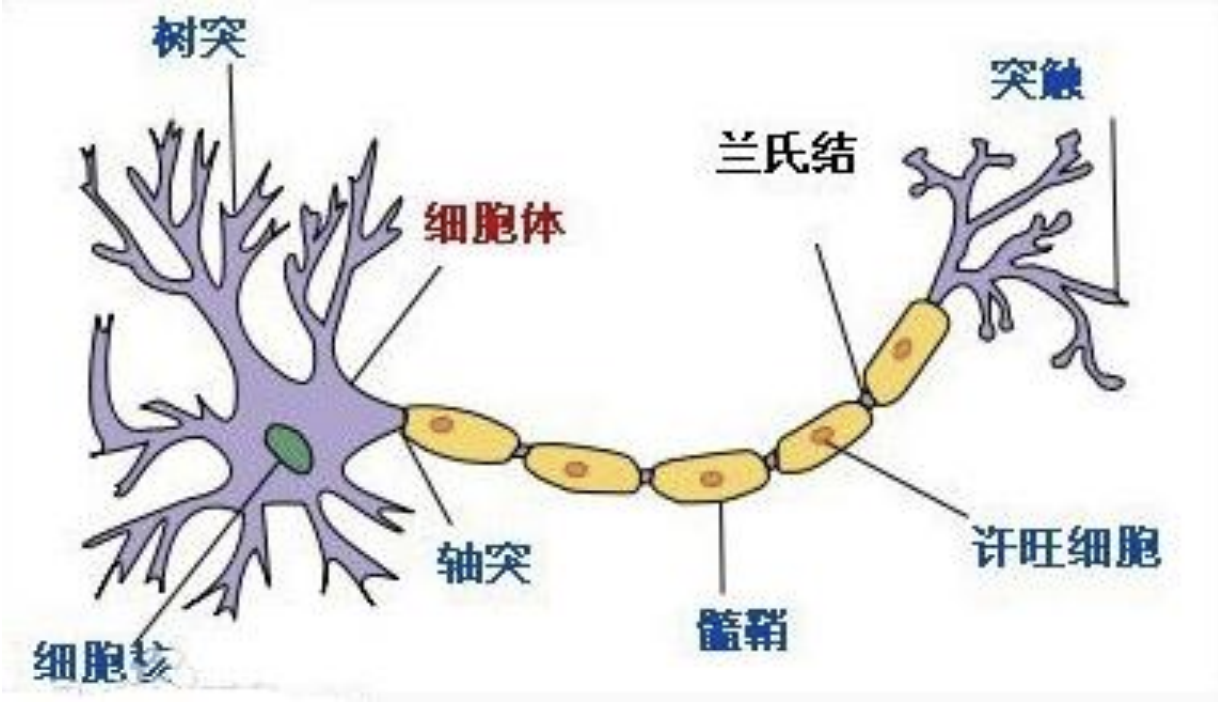
显然计算机中的神经元算是一种仿生学设计. 在生物学上, 树突进行信号的输入, 轴突进行信号的输出

  • 神经元内化学物质调节内部电位, 跨膜电位达到一个阈值时, 则激活或放电, (固定)时间和强度的脉冲传递给轴突

  • 轴突像树枝状, 连接到突触

1.2. $\text{Hebb}$'s Law

加拿大生理心理学家 $\text{Donald Olding Hebb}$ (1904-1985)

  • 连接强度调整量与输入输出的乘积成正比, 显然经常出现的模式将增强神经元之间的连接

  • 与巴普洛夫的’条件反射’一致

  • 又称为”长程增强机制”(LTP, Long Term Potentiation)或”神经可塑”(Neural Plasticity)

1.3. History

1943年, 心理学家 $\text{W. McCulloch}$ 和数理逻辑学家 $\text{W. Pitts}$ 首次提出神经元的数学模型: $\text{M-P}$ model

1948年, $\text{Von.Neumann}$ 提出相互再生自动机网络结构

1957年, $\text{F. Rosenblatt}$ 提出 Perceptron model

1960s, $\text{Widrow}$ 提出非线性多层自适应网络

1968年, $\text{Minsky}$ 发表 Perceptron 一书

1982年和1984年, 物理学家 $\text{Hopfield}$ 在美国科学院院刊上发表ANN文章

2006年, $\text{Hinton}$ 发表深度信念网络 $\to$ 深度学习

1.3. $\text{M-P}$ Neuron

$\text{M-P}$ Neuron 的设计高度还原了神经元的工作机制. 对于第 $i$ 个神经元的输入 $x_i$ 以及对应的权重 $\omega_i$, 有

$$\begin {align} \boldsymbol {x}=(x_1,x_2,\ldots,x_n)^{\mathsf T}\\ \boldsymbol w=(w_1,w_2,\ldots,w_n)^{\mathsf T} \end {align} $$

再考虑上阈值 $\theta$ , 激活函数 $f$ 和输出 $y$, 我们有

$$y=f\left(\boldsymbol w^{\mathsf T}\boldsymbol x-\theta\right) $$

具体的示意图如下:

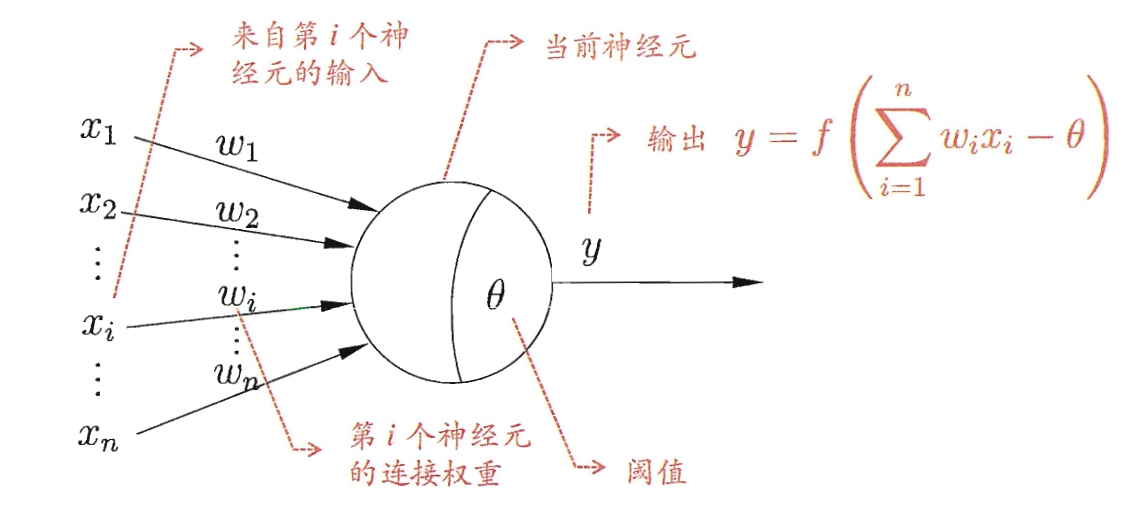
值得注意的是, 权重具有其生物学意义:

  • 兴奋性连接: 权重为正
  • 抑制性连接: 权重为负

理想情况下, 我们希望激活函数 $f$ 就是跃迁函数 $\operatorname{sgn}(x)$.

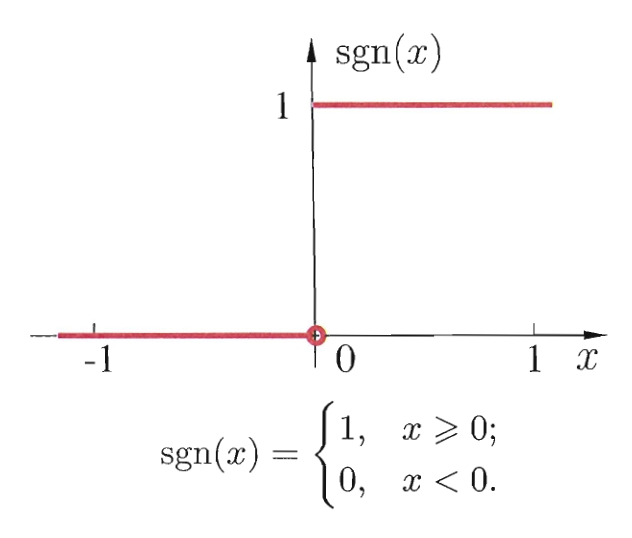
然而 $\operatorname{sgn}(x)$ 不连续不光滑, 不利于我们的后续计算. 因此我们更常用 $\operatorname{sigmoid}(x)$ 作为激活函数 (加上挤压参数 $\lambda$ )

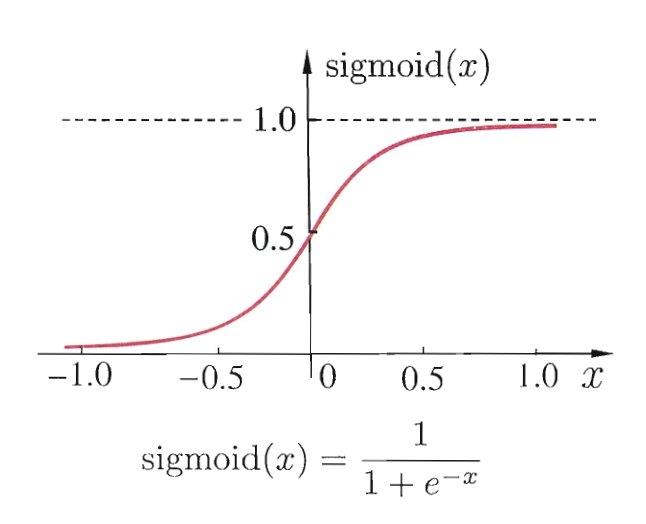
2. Perceptrons and Perceptron Learning

2.1. Perceptron

感知机 (Perceptron) 是最简单形式的前馈式人工神经网络, 它仅由两层神经元构成, 是一种二元线性分类器, 使用特征向量作为输入, 把矩阵上的输入 $\boldsymbol x$ (实数值向量)映射到输出值 $f(\boldsymbol x)$ 上 (一个二元的值)

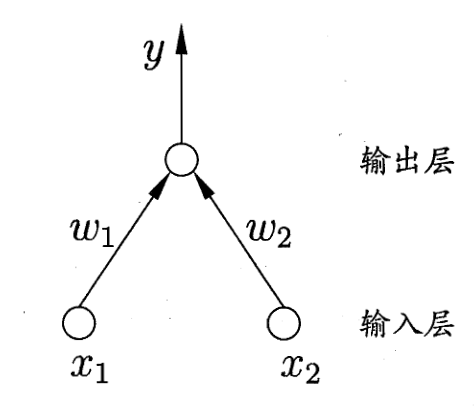
最简单的感知机结构

感知机具有这样的性质:

  • 同层内无互连

  • 不同层间无反馈

  • 由下层向上层传递

  • 输入输出均为离散值

  • 由阈值函数决定其输出

2.2. Perceptron Learning

我们发现更一般地, 给定训练数据集, 权重 $\boldsymbol w=(w_1,w_2,\ldots,w_n)^{\textbf T}$ 以及阈值 $\theta$ 可通过学习得到. 國值 $\theta$ 可看作一个固定输入为 -1 的 “哑结点” (dummy node) 所对应的连接权重 $w_{n+1}$. 这样, 权重和网值的学习就可统一为权重的学习. 感知机学习规则非常简单, 对训练样例 $(\boldsymbol x, y)$, 若当前感知机的输出为 $\hat y$, 则感知机权重将这样调整：

$$\left\{ \begin{array}{cc} w_{i} \leftarrow w_{i}+\Delta w_{i} \\ \Delta w_{i}=\eta(y-\hat{y}) x_{i} \end{array} \right. $$

其中 $\eta\in(0,1)$ 称为学习率 (learning rate)

总的来说, 感知机的学习包括如下的过程:

  1. 权值初始化

  2. 输入样本对

  3. 计算输出

  4. 根据感知机学习规则调整权重

  5. 返回到步骤2输入到下一对样本, 直至对所有样本的实际输出与期望输出相等

3. Linear separability

关于是否线性可分的问题很多, 具体还查看这篇文章

3.1. Decision Boundary

需注意的是, 感知机只有输出层神经元进行激活函数处理, 即只拥有一层功能神经元 (functional neuron), 其学习能力非常有限. 事实上, 根据 Perceptron 收敛理论, 可以证明 (IMinsky and Papert,1969):

若两类模式是线性可分的, 即存在一个线性超平面能将它们分开, 则感知机的学习过程一定会收敛 (converge) 而求得适当的权向量 $\boldsymbol w=(w_1,w_2,\ldots,w_n,w_{n+1})^{\textbf T}$ 否则感知机学习过程将会发生振荡 (Auetuation), $\boldsymbol w$ 难以稳定下来, 不能求得合适解.

例如如下图的异或问题.

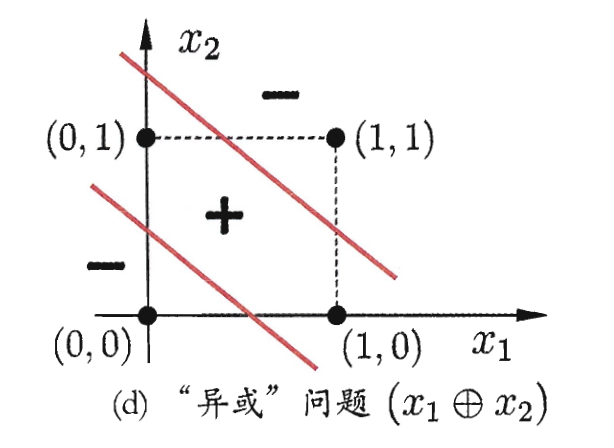
实际上, 定义 $\gamma$ 是分离超平面与最接近的数据点之问的距离, 则迭代次数的界是 $\displaystyle \frac 1 {\gamma^2}$

对于多分类问题, 每一个输出神经元定义一条决策边界, 多个神经元就决定了多分类的决策边界

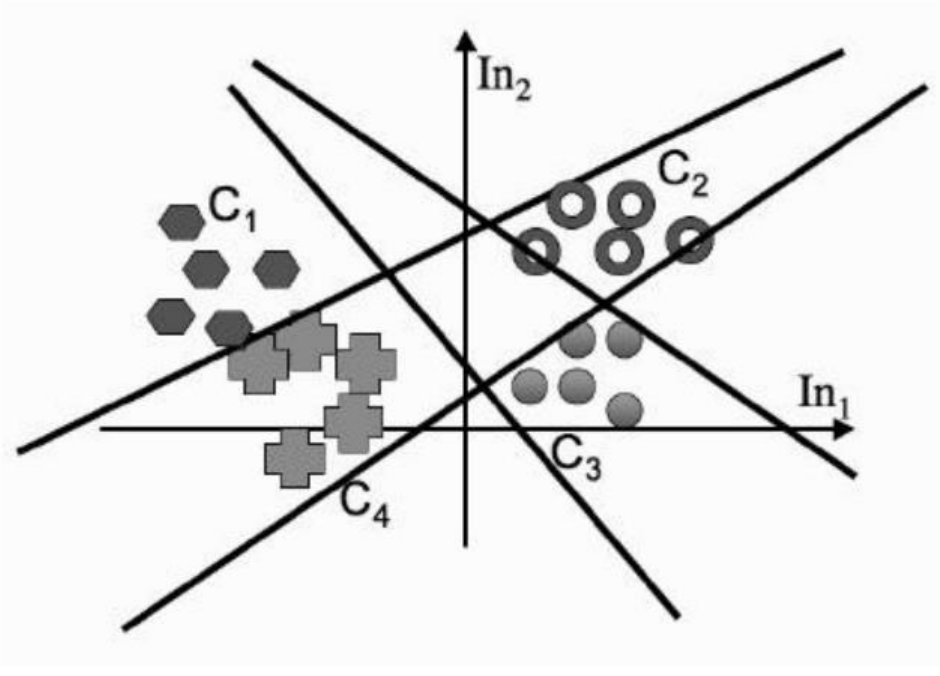
3.2. Non-linear Separable

对于线性不可分的问题, 我们可以考虑使用这篇文章中的数据升维技巧, 也可以考虑使用多层网络 (但我认为两者本质没什么区别).

下图介绍了一种使用多层网络来处理线性不可分问题的方法.

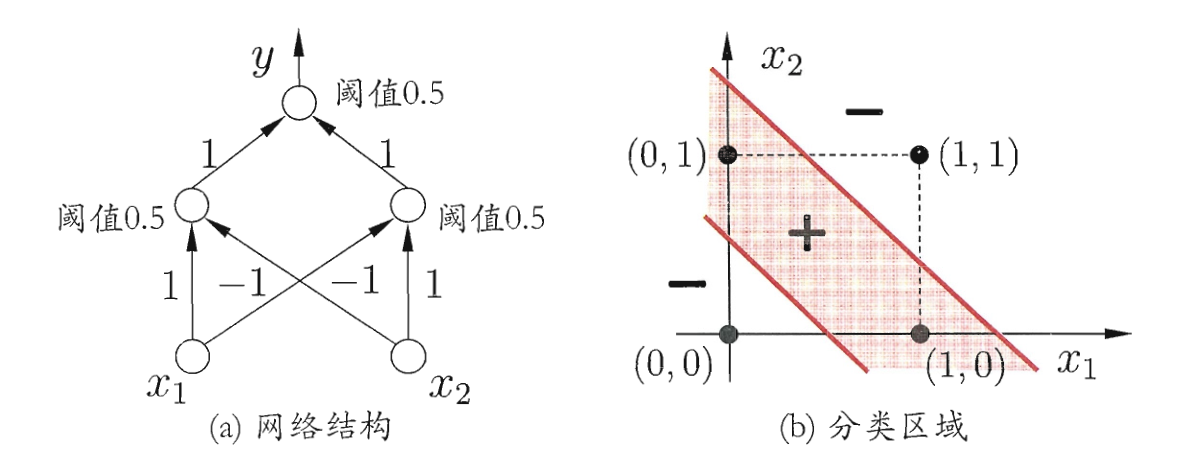
感知器表示与, 或, 与非, 或非的能力是很重要的, 因为所有的布尔函数都可表示为基于这些原子函数的互连单元的某个网络.

事实上, 仅用两层深度的感知器网络就可以表示所有的布尔函数, 在这些网络中输入被送到多个单元, 这些单元的输出被输入到第二级, 也是最后一级.

因为阈值单元的网络可以表示大量的函数, 而单独的单元不能做到这一点, 所以通常我们感兴趣的是学习阈值单元组成的多层网络.