Musical Scales

GE › Physics in the Arts

Reference:
Wikipedia and Physics in the Arts by P.U.P.A. Gilbert and W.J. Gilbert

1. Numerous Definitions & Notations

  1. 一些生词
    • pitch: 音高
    • tone: 音调
    • tune: 曲调 (由音调组成)
  2. Musical Scale (音阶): a set of pitches (or frequencies) that are used in music.
    • Major Scale (大调): a diatonic scale with a specific pattern of whole and half steps.
    • Diatonic Scale (自然音阶): a heptatonic scale that includes five whole steps and two half steps in each octave.
  3. Octave (八度): the interval between one musical pitch and another with half or double its frequency.
  4. Note (音符🎵): either to denote the symbols that represent the tones of the scale on paper or the tones themselves.
  5. Polyphony (复调): the simultaneous combination of two or more tones or melodic lines.
  6. Consontance (和谐): a consonant interval or chord is one in which the frequencies of the component tones are in simple integer ratios.
  7. Chord (和弦): a group of (typically three or more) notes sounded together, as a basis of harmony.

2. Musical Intervals

音程

A musical interval is characterized by the ratio of the two frequencies. Intervals sound the same if they have the same frequency ratios.

$\textbf{Examples}$ of musical intervals:

  • A 2:1 ratio is called the octave: The interval from 200 Hz to 400 Hz sounds the same as the interval from 300 Hz to 600 Hz.

  • A 3:2 ratio is called a fifth: The interval from 200 Hz to 300 Hz sounds the same as the interval from 300 Hz to 450 Hz.

    • If its a 2:3 ratio, we call it go down a fifth

  • A 5:4 ratio is called a major third: In the preceding example (“Are you sleeping . . . ”), the third tone (“sleep-”) is a major third above the first (“Are”).

  • A 6:5 ratio is called a minor third.

3. Consonance (Harmony): Simple Number Ratios

The establishment of a musical scale is a cultural development that extends over centuries and involves subjective preferences. However, one finds that all cultures seem to have a preference for certain musical intervals (frequency ratios), like the octave, the fifth and other simple-number ratios. The preference for simple-number ratios quite likely is related to the fact that in most music two or more tones are heard simultaneously.

Not all polyphonic combinations of tones are equally pleasing to the ear. The most pleasing combinations are called consonances. The most dissonant combinations are called dissonances.

But what combinations of frequencies are consonant?

Simple-number frequency ratios are consonant (“in harmony”) because the various partials of the two tones being played simultaneously either coincide exactly or are different enough to avoid beats or roughness.

Roughness comes about when two frequencies are near one another but not so close that one discerns the beats individually (e.g., 400 Hz and 410 Hz). For example, two tones a fifth apart, such as 200 Hz and 300 Hz are consonant because the partials of one (200, 400, 600, 800, 1000, 1200 Hz) and of the other (300, 600, 900, 1200 Hz) have a particular relationship: Some partials coincide exactly (here 600, 1200 Hz), while the others are so different that they produce no roughness. This of course would not be the case for a detuned fifth, such as 200 Hz and 305 Hz, since now the third partial of 200 Hz (600 Hz) clashes with the second partial of 305 Hz (610 Hz).

To repeat: Tones with simple number ratios of frequencies are consonant because of absence of beats or roughness between their higher partials. We said “simple number ratios,” but how simple do they need to be? An experiment shows that 6:5 is perceived as consonant (in earlier times it was considered dissonant!), while already 9/8 is not and 16:15 is very dissonant!

4. The Major Triad

A “triad” is a set of three tones often played together as a “chord.”

Frequencies of the major triad is

$$\left\{1, \frac{5}{4}, \frac{3}{2}\right\} $$

An example is the major triad C-E-G, where the frequencies are in the ratio 1:5/4:3/2. The major triad is a consonant chord because the frequencies of the tones are in simple-number ratios.

5. Constucting Musical Scales

Besides C-E-G, there are other consonant triads, such as D-F-A and E-G-B. These three triads are the basis of the major scale.

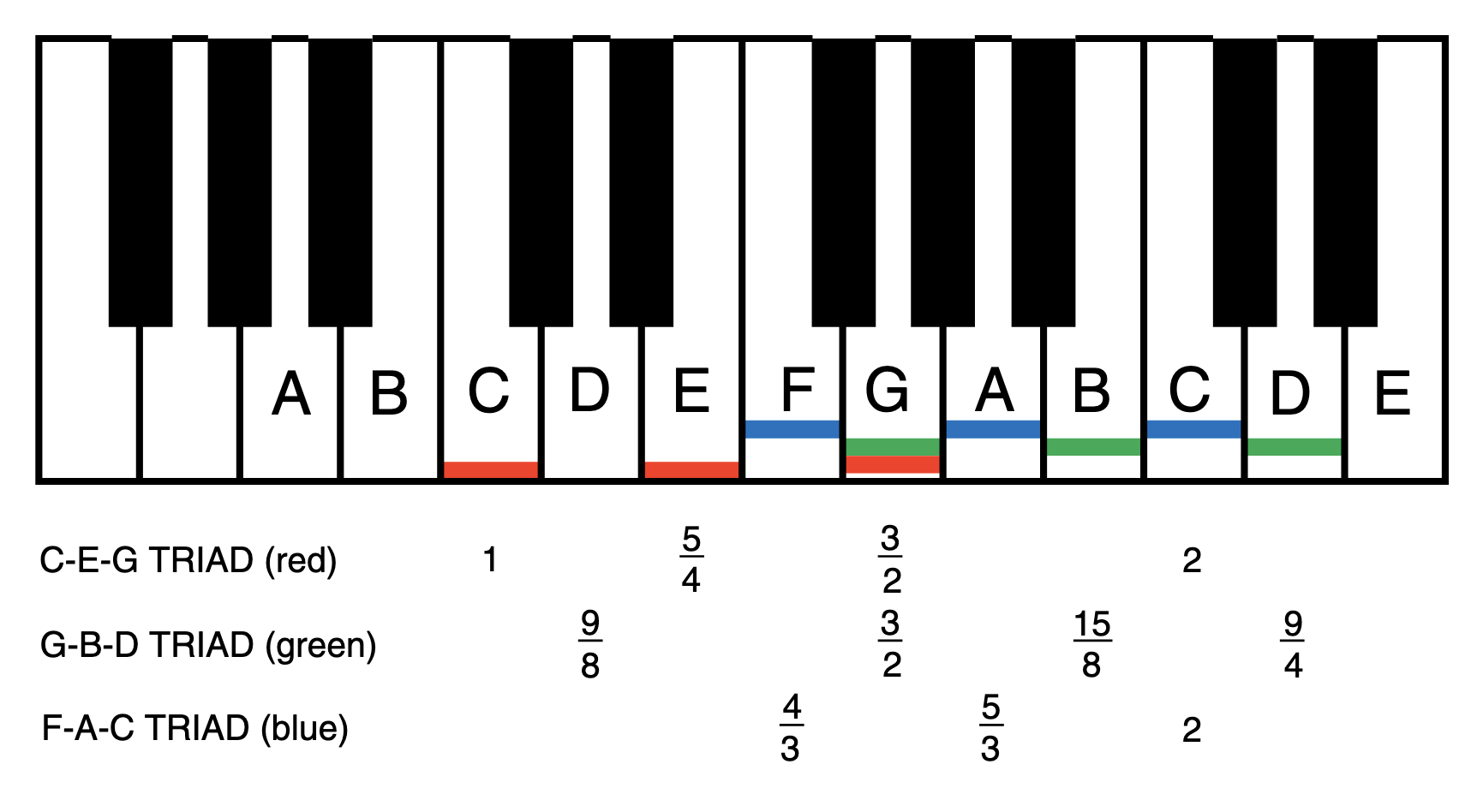
6. Hole and Half Tone Intervals

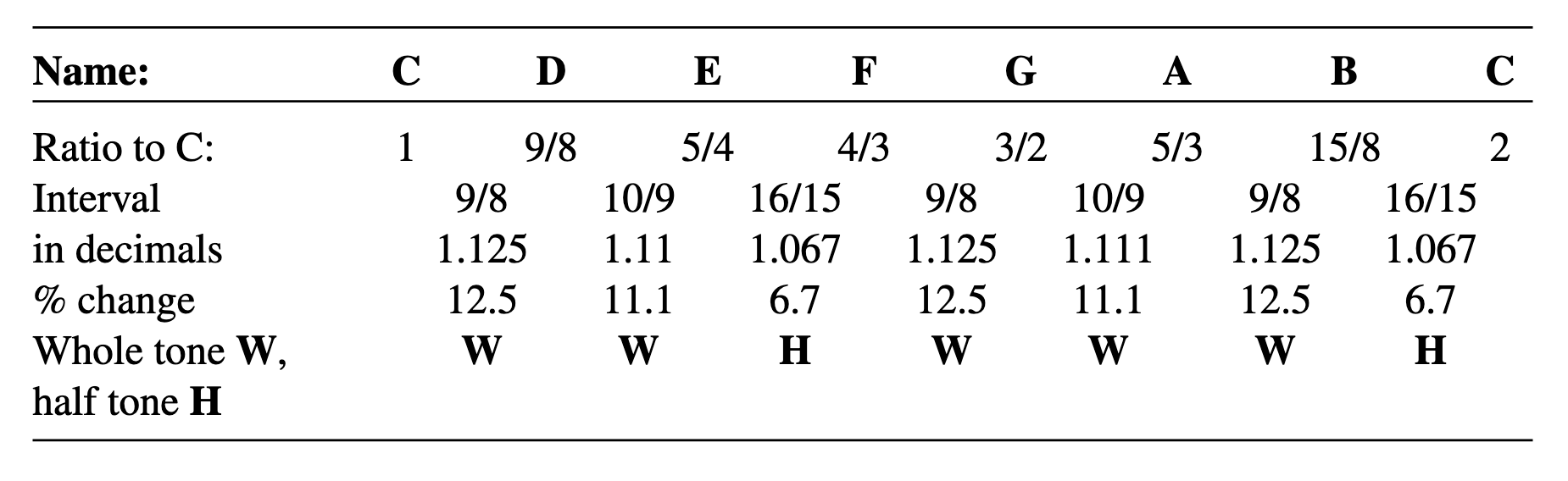
we may call the whole- and half-tones 1 and 1/2. Any sequence of tones that has this particular pattern of intervals:

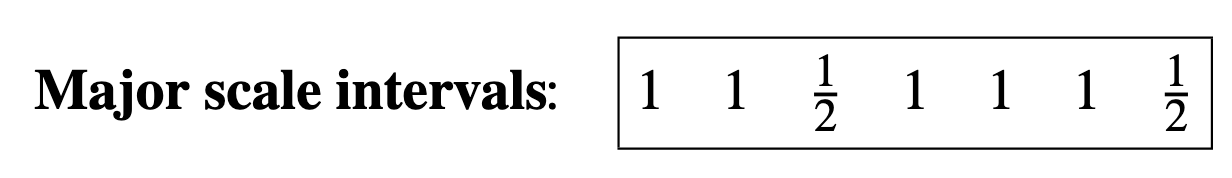
is called a major scale. Depending on the tuning of the instrument, the frequencies may differ a little bit from the just tuning, what is important here is that there are two kinds of intervals, large and small. Scales using two kinds of intervals, large and small, are called diatonic scales.

$\textbf{Example}$ of a diatonic scale:

  • The C-major scale is C-D-E-F-G-A-B-C.
  • The D-major scale is D-E-F#-G-A-B-C#-D.

7. Names of Intervals