1. Intro
线性分类可以进行如下的区分:
- 硬分类 $y\in\left\{0,1\right\}$
- LDA (Linear Discriminant Analysis)
- Perceptron (感知机)
- 软分类 $y\in[0,1]$
- 概率生成模型:
- $\text{Gaussian}$ Discriminant Analysis
- Naive $\text{Bayes}$
- 概率判别模型: Logistic Regression
我们将主要考察二分类模型. 也就是主要考虑逻辑回归 (logistic regression) 和 $\text{Fisher}$ 线性判别分析两种分类算法;
2. Binary Classification
2.1. Necessity
在多重线性回归分析中, 我们主要使用OLS和GLS来构造线形回归的模型.
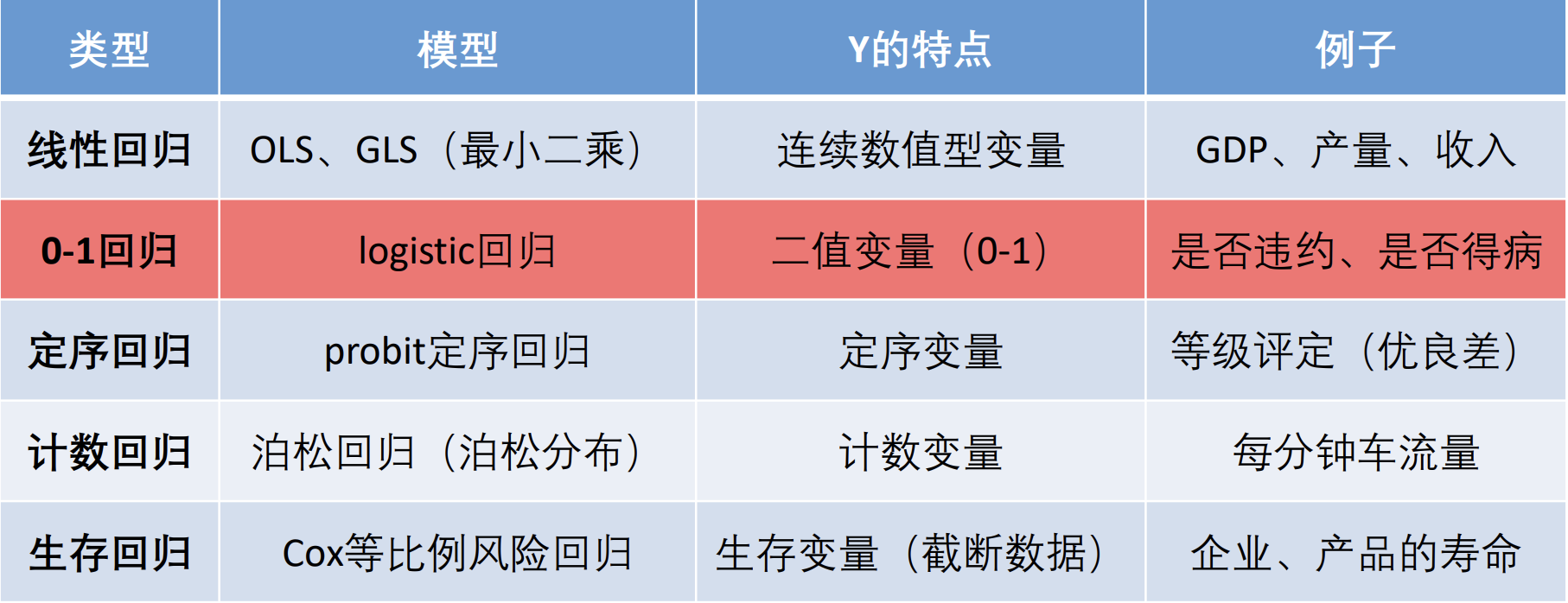
现在, 我们很自然地也想尝试, OLS 和 GLS 方法能否用来构造 $\text{0-1}$ 回归. 也就是说, 如果存在这样一个回归模型, 能够将我给出的数据分成0和1两类, 那就很自然地达到了二回归的效果. 实际上, OLS 模型不能构造出一个 $\text{0-1}$ 回归.
我们可以进行一个简单的验证. 假设一个线性概率模型 (Linear Probability Model, PLM) 能够用来构造 $\text{0-1}$ 回归. 那我们假设
$$y_{i}=\beta_{0}+\beta_{1} x_{1 i}+\beta_{2} x_{2 i}+\cdots+\beta_{k} x_{k i}+\mu_{i}
$$
也即:
$$y_{i}=\boldsymbol{x}_{\boldsymbol{i}}^T \boldsymbol{\beta}+u_{i}\quad(i=1,2, \cdots, n)
$$
由于 $y_i$ 只能取 $0$ 或者 $1$,
$$u_{i}=\left\{\begin{array}{cc}1-\boldsymbol{x}_{\boldsymbol{i}}^T \boldsymbol{\beta} & , y_{i}=1 \\ -\boldsymbol{x}_{\boldsymbol{i}}^T \boldsymbol{\beta} & , y_{i}=0\end{array}\right.
$$
显然发现 $\operatorname{Cov}(u_i,x_i)\not=0$. 那么根据假设, 我们得到这样的回归方程:
$$\widehat{y_{i}}=\widehat{\beta_{0}}+\widehat{\beta_{1}} x_{1 i}+\widehat{\beta_{2}} x_{2 i}+\cdots+\widehat{\beta_{k}} x_{k i}
$$
但是预测值却可能出现 $\hat y_i>1$ 或 $\hat y_i<0$ 的情况 (内生性).
2.2. Link Function
那么很自然地, 我们希望有一个映射, 能将 $\widehat {y_i}$ 映射到 $[0,1]$ 上.
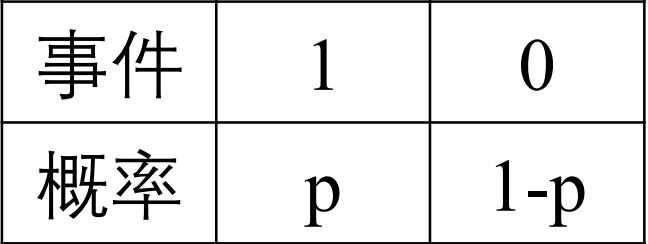
假设这样的映射叫 $F$, 那么:
$$\left\{\begin{array}{l}P(y=1 \mid \boldsymbol{x})=F(\boldsymbol{x}, \boldsymbol{\beta}) \\ P(y=0 \mid \boldsymbol{x})=1-F(\boldsymbol{x}, \boldsymbol{\beta})\end{array}\right.
$$
其中, $F(\boldsymbol{x}, \boldsymbol{\beta})=F\left(\boldsymbol{x}_{\boldsymbol{i}}^T \boldsymbol{\beta}\right)$. $F$ 被称为连接函数 (link function).
具体来说, 连接函数可以取包括但不限于如下的两种:
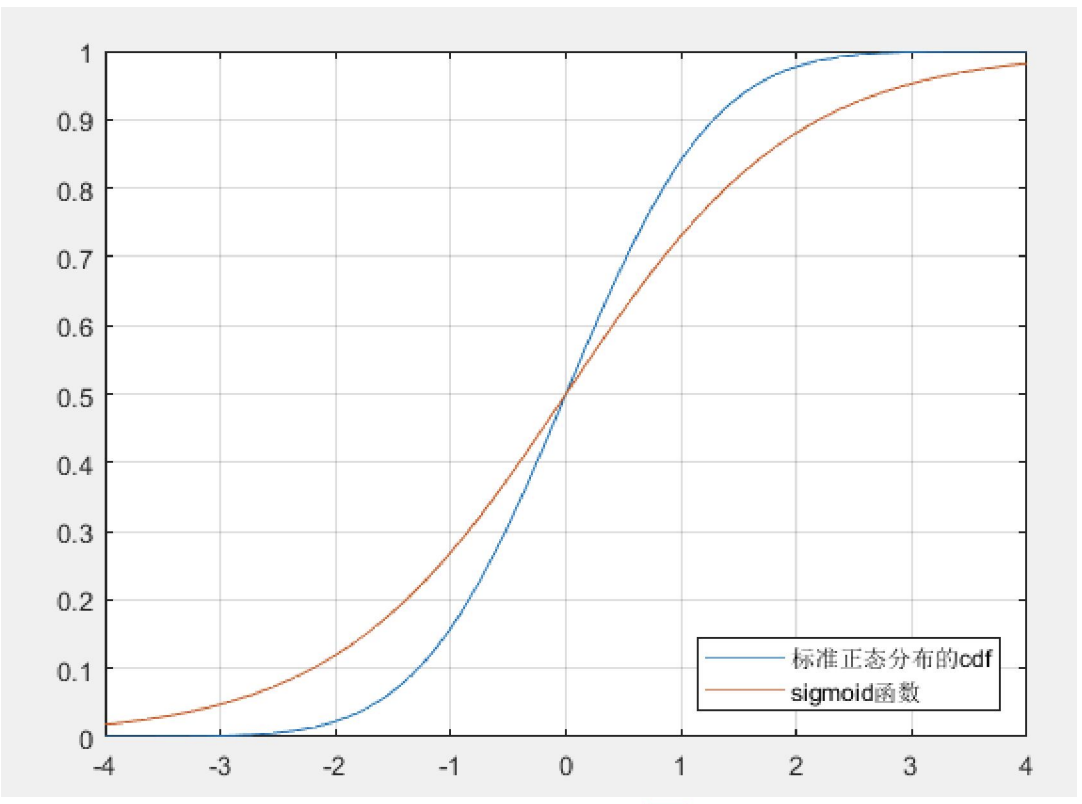
- 标准正态分布的累积密度函数 (probit 回归):
$$F(\boldsymbol{x}, \boldsymbol{\beta})=\Phi\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)=\int_{-\infty}^{x_{i}^{\prime} \boldsymbol{\beta}} \frac{1}{\sqrt{2 \pi}} e^{-\frac{t^{2}}{2}} d t
$$
- $Sigmoid$ 函数 (logistic回归):
$$F(\boldsymbol{x}, \boldsymbol{\beta})=S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)=\frac{\exp \left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)}{1+\exp \left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)}
$$
由于后者有解析表达式 (而标准正态分布的累积密度函数没有), 所以计算 logistic 模型比 probit 模型更为方便.
2.3. Logistic Regression
对于给定的函数
$$F(\boldsymbol{x}, \boldsymbol{\beta})=S\left(\boldsymbol{x}_{\boldsymbol{i}}’\boldsymbol{\beta}\right)=\frac{\exp \left(\boldsymbol{x}_{\boldsymbol{i}}’\boldsymbol{\beta}\right)}{1+\exp \left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)}\quad \boldsymbol x_i'=\boldsymbol x_i^T
$$
我们考虑对样本进行极大似然估计 (MLE):
在笔者的这篇数据科学笔记中对极大似然估计给出了具体的论述.
$$\left\{\begin{array}{l}P(y=1 \mid \boldsymbol{x})=S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right) \\ P(y=0 \mid \boldsymbol{x})=1-S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\end{array} \quad \Rightarrow f\left(y_{i} \mid \boldsymbol{x}_{\boldsymbol{i}}, \boldsymbol{\beta}\right)=\left\{\begin{array}{ll}S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right), & y_{i}=1 \\ 1-S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right), & y_{i}=0\end{array}\right.\right.
$$
写成更加紧凑的形式并取对数:
$$\begin{aligned} f\left(y_{i} \mid \boldsymbol{x}_{\boldsymbol{i}}, \boldsymbol{\beta}\right) & =\left[S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]^{y_{i}}\left[1-S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]^{1-y_{i}} \\ \ln f\left(y_{i} \mid \boldsymbol{x}_{\boldsymbol{i}}, \boldsymbol{\beta}\right) & =y_{i} \ln \left[S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]+\left(1-y_{i}\right) \ln \left[1-S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]\end{aligned}
$$
样本的对数似然函数如下:
$$\ln L(\boldsymbol{\beta} \mid \boldsymbol{y}, \boldsymbol{x})=\sum_{i=1}^{n} y_{i} \ln \left[S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]+\sum_{i=1}^{n}\left(1-y_{i}\right) \ln \left[1-S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \boldsymbol{\beta}\right)\right]
$$
我们考虑使用梯度下降法这一数值方法来解决这个非线性最大化问题. 有考虑到如下的等式:
$$E(y \mid \boldsymbol{x})=1 \times P(y=1 \mid \boldsymbol{x})+0 \times P(y=0 \mid \boldsymbol{x})=P(y=1 \mid \boldsymbol{x})
$$
因此 $\hat y_i$ 就是 $y_i=1$ 发生的概率. (一般和0.5进行比较)
$$\widehat{y}_{i}=P\left(y_{i}=1 \mid \boldsymbol{x}\right)=S\left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \widehat{\boldsymbol{\beta}}\right)=\frac{\exp \left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \widehat{\boldsymbol{\beta}}\right)}{1+\exp \left(\boldsymbol{x}_{\boldsymbol{i}}^{\prime} \widehat{\boldsymbol{\beta}}\right)}=\frac{e^{\widehat{\beta}_{0}+\widehat{\beta}_{1} x_{1 i}+\widehat{\beta}_{2} x_{i i}+\cdots+\widehat{\beta}_{k} x_{i i}}}{1+e^{\widehat{\beta}_{0}+\widehat{\beta}_{1} x_{i n}+\widehat{\beta}_{2} x_{2 i}+\cdots+\widehat{\beta}_{k} x_{i k}}}
$$
2.4. Overfitting
过拟合现象
虽然预测能力提高了, 但是容易发生过拟合的现象. 对于样本数据的预测非常好, 但是对于样本外的数据的预测效果可能会很差. (类似于之前提到的 $\text{Runge}$ 现象)
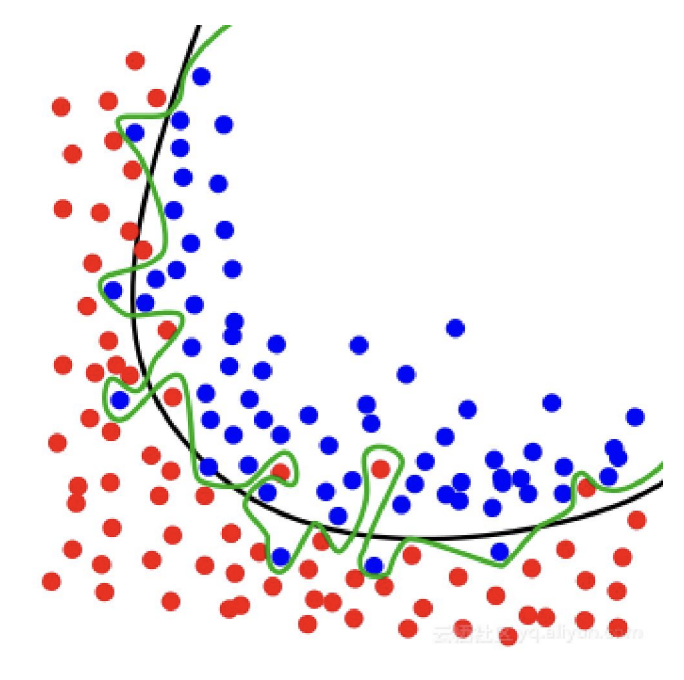
为了确定合适的模型, 我们一般把数据分为训练组和测试组, 用训练组的数据来估计出模型, 再用测试组的数据来进行测试. (训练组和测试组的比例一般设置为 80% 和 20%). 为了消除偶然性的影响, 可以对上述步骤多重复几次, 最终对每个模型求一个平均的准确率. 这个步骤称为**交叉验证**.
2.5. $\text{Fisher}$ Linear Discriminant Analysis
关于LDA, 笔者在他的这篇数据科学笔记中进行了相对详细的介绍
LDA (Linear Discriminant Analysis)是一种经典的线性判别方法, 又称 $\text{Fisher}$ 线形判别分析. 该方法思想比较简单: 给定训练集样例, 设法将样例投影到一维的直线上, 使得同类样例的投影点尽可能接近和密集, 异类投影点尽可能远离.
3. Multi-class Classification



