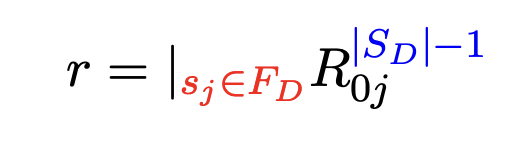Lexical Analysis

CS › Compilers

1. Lexer介绍

1.1. Lexer的功能

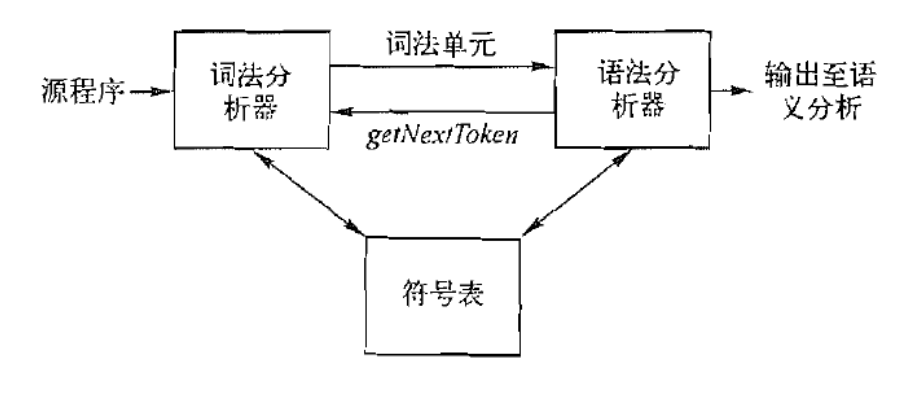
ANTLR4中的g4文件和ANTLR3中的g文件, 都是词法单元的规约

1
2
3
4
graph LR
  程序文本/字符串s -->|输入| Lexer
	词法单元的规约 --> |输入| Lexer
	Lexer --> |输出|词法单元流

1.2. 词法分析器的三种设计方法

难度递增

  • Lexer Generator (e.g. ANTLR4)
  • Handwritten Lexer
  • Automated Lexer

生产环境下的编译器 (如 gcc) 通常选择手写词法分析器

2. 词法单元的规约

词法单元的规约需要 形式化 定义

2.1. 非形式化的定义

  1. id: 以字母开头的字母/数字串
  2. Language: id 所构成的集合
  3. Definition of Language: 给定 Alphabet $\Sigma$ 上一个任意的可数的 String 集合
Language

(3) Alphabet: 字母与数字等符号的集合

  • $def$: Alphabet $\Sigma$ 是一个有限的符号集合.
alphabet

(4) String: 语言中的每一个元素(即一个id)称为串

  • $def$: Alphabet $\Sigma$ 上的 String (s) 是由 $\Sigma$ 中符号构成的一个有穷序列.

  • 特殊地, 空串 $\epsilon$ 是满足 $|\epsilon|=0$ 的串

String 上定义了两种运算

  • 连接运算: 如果 $x$ 和 $y$ 都是一个 String, 则
$$(x = dog\ \wedge \ y = house) \ \Rightarrow xy = doghouse $$
  • 指数运算: 如果$s$ 是一个 String, 则
$$\begin{align} s^0 &:= \epsilon\\ s^i &:=ss^{i-1},\ i\geq 1 \end{align} $$

根据上述的四个定义, 我们不难发现: 语言是串的集合

2.2. 形式化的定义

语言形式化的定义, 我们借助了集合的概念. 对于集合的运算, 我们首先需要回顾闭包的概念, 闭包允许我们通过有限集构造出无限集

正闭包与Kleene闭包

常见的集合运算

这里的连接应该是一种类似于 Descartes积的东西

我们发现, 如果 $\mathbf L := \{A, B, . . . , Z, a, b, . . . , z\},\mathbf D:=\{= 0, 1, . . . , 9\} $, 那么根据集合运算的定义, id 可以形式化地定义为:

$$\mathbf {id}:= \mathbf {L(L \cup D)^*} $$

接下来要引入 (简洁、优雅、强大的) 正则表达式.

2.3. 正则表达式的形式化定义

每个正则表达式 $r$ 对应着一个正则语言, 记作 $L(r)$. 给定字母表 $\Sigma$, $\Sigma$ 上的正则表达式以及对应的正则语言由且仅由如下的4条规则定义:

  1. $\epsilon$ 是正则表达式:
$$L(\epsilon):=\{\epsilon\} $$
  1. $\forall a\in \Sigma$, $a$ 是正则表达式:
$$\forall a\in \Sigma, L(a):=\{a\} $$
  1. 如果 $r$ 是正则表达式, 则 $(r)$ 也是正则表达式:
$$L((r))=L(r) $$
  1. 如果 $r$ 与 $s$ 是正则表达式, 则 $r|s$, $rs$, $r^*$ 也是正则表达式:
$$\begin{align} L(r|s) &=L(r)\cup L(s)\\ L(rs) &=L(r)L(s)\\ L(r^*) &=(L(r))^* \end{align} $$

其中, 运算优先级满足

$$() \ \color {red} {\succ} \color{black} \ ^*\ \color{red}\succ\color{black}\ \text{连接} \ \color{red}\succ\color{black}\ | $$
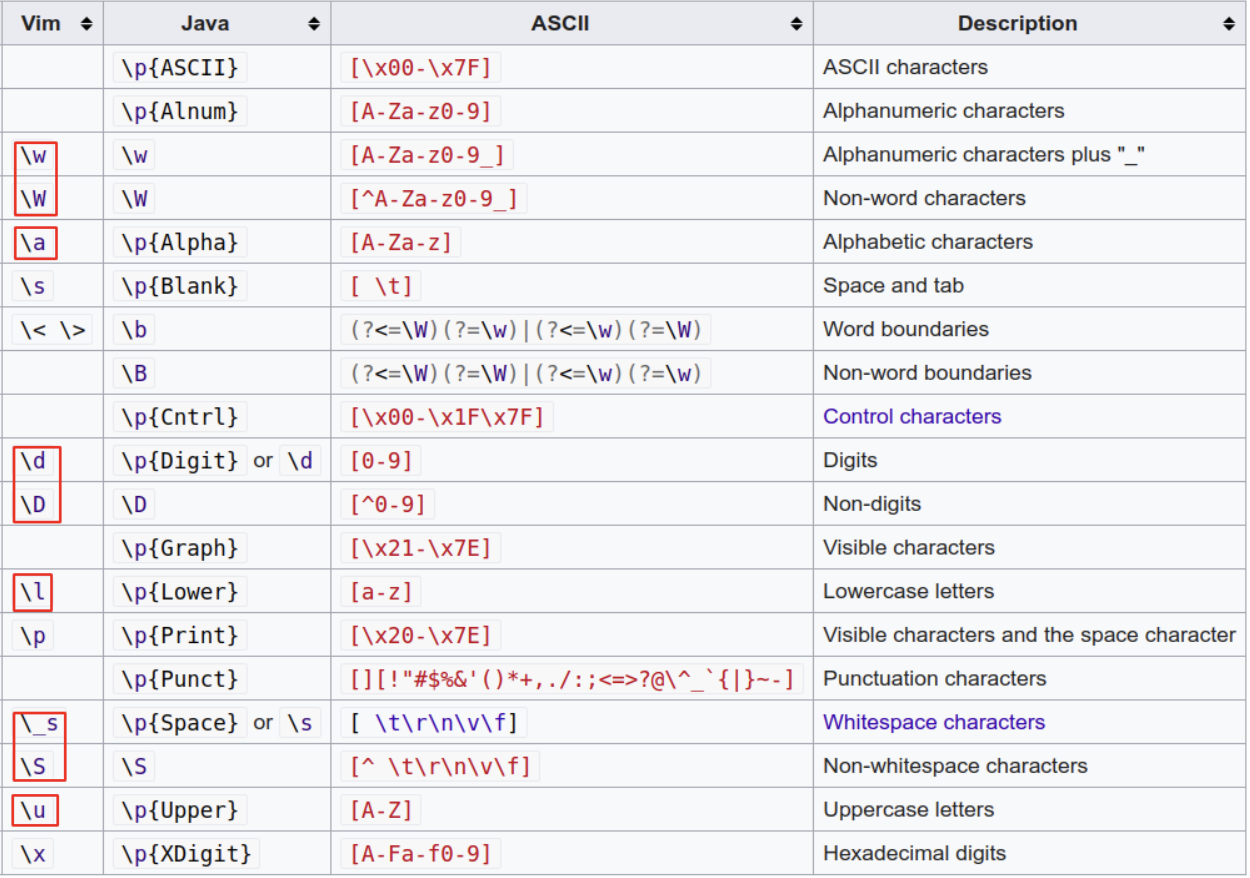
正则表达式简记法

3. Lexer Generator—— ANTLR4

3.1. ANTLR4中的冲突解决规则

这篇文章介绍了贪婪匹配和非贪婪匹配的区别

  • 最前优先匹配
  • 最长优先匹配
    • 1.23不会被匹配成1, ., 23
    • >=不会被匹配成 > 和 =
  • 非贪婪匹配
  • 在默认情况下的量词匹配都是贪婪匹配, 只需要在量词后加上?, 就会转变为非贪婪匹配
  • ANTLR4采用这样的非贪婪匹配

4. Automated Lexer

4.1. Definitions

自动机(Automaton; Automata) 的两大要素: 状态集 $S$ 和状态转移函数 $\delta$

‘开关’自动机

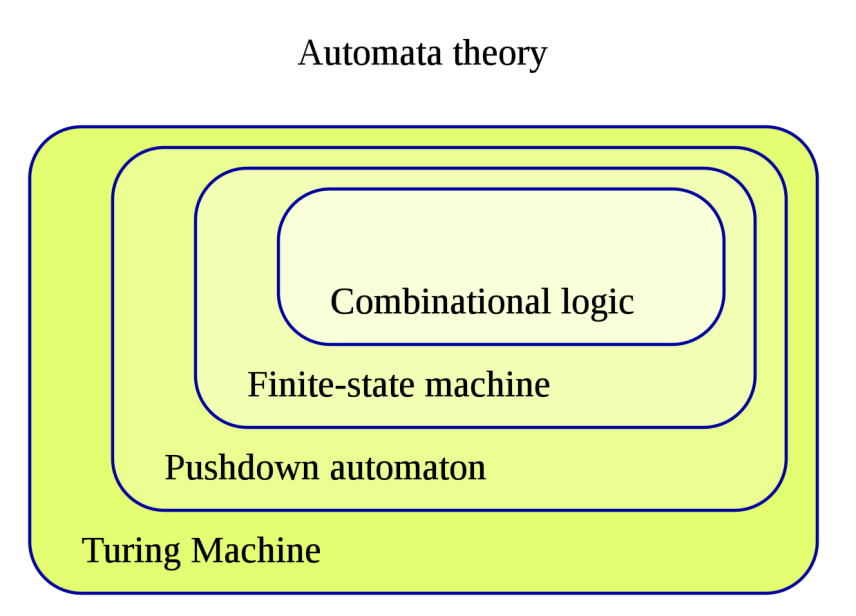
在自动机理论中, 根据表达/计算能力的强弱, 自动机可以分为不同层次.

自动机的常见层次

在接下来的全部内容中, 我们将试图生成一个正则表达式的词法分析器 (也就是说, 下面的定义可能有其狭义之处).

NFA

$def$: 非确定性有穷自动机 (Nondeteministic Finite Automaton) $\mathcal A$ 是一个五元组:

$$\mathcal A:=(\Sigma, S, s_0, \delta, F) $$

where:

(1) $\Sigma$ 是字母表 ($\epsilon \not \in \Sigma$)

(2) $S$ 是有穷的状态集合

(3) $s_0$ 是唯一的初始状态, $s_0 \in S$

(4) $\delta$ 是状态转移函数:

$$\delta : S \times (\Sigma \ \cup \{\epsilon\})\rightarrow 2^S $$

(5) $F$ 是接受状态的集合, $F\subseteq S$

约定: 所有没有对应出边的字符默认指向一个默认不存在的 “空状态” $∅$

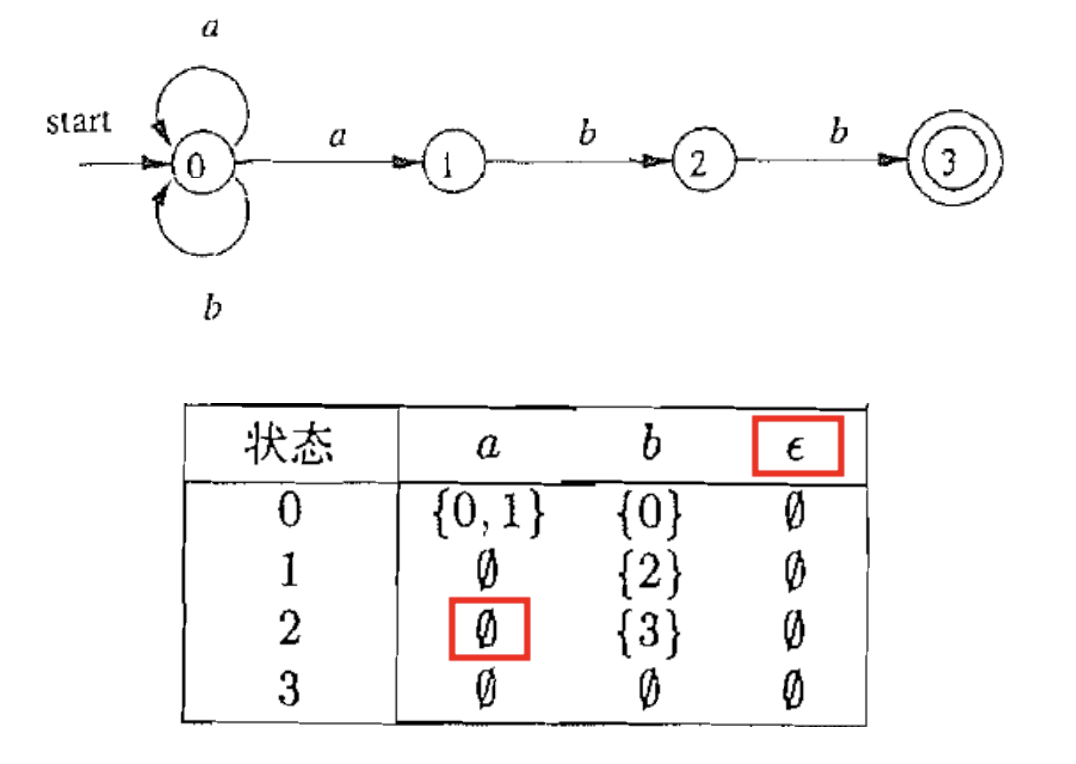
imgsimage-20230411142523855

(非确定性) 有穷自动机是一类极其简单的计算装置 它可以识别 (接受/拒绝) $\Sigma$ 上的字符串

Accept

$def$: NFA $\mathcal A $ 接受String $x$, 当且仅当存在一条从开始状态 $s_0$ 到某个接受状态 $f\in F$, 标号为 $x$ 的路径.

根据这样的定义, $\mathcal A$ 定义了一种语言 $L(\mathcal A)$: 即所有能被 $\mathcal A$ 接受的字符串所构成的集合

在上面的例子中, $\mathcal A$ 的语言 $L(\mathcal A)$ 就是如下的正则表达式定义的正则语言:

$$L(\mathcal A)=L((a|b)^*abb) $$

DFA

$def$: 确定性有穷自动机 (Deteministic Finite Automaton) $\mathcal A$ 是一个五元组:

$$\mathcal A:=(\Sigma, S, s_0, \delta, F) $$

其中:

(1) $\Sigma$ 是字母表 ($\epsilon \not \in \Sigma$)

(2) $S$ 是有穷的状态集合

(3) $s_0$ 是唯一的初始状态, $s_0 \in S$

(4) $\delta$ 是状态转移函数:

$$\delta: S \times \Sigma\rightarrow 2^S $$

(5) $F$ 是接受状态的集合, $F\subseteq S$

约定: 所有没有对应出边的字符默认指向一个 “死状态”

直觉上, DFA 和 NFA 的区别在于, DFA 的每一个节点的出边都是确定的, 不会存在对于一个节点, 给定一个输入, 但是进入到两个不同状态的情况

相比之下 NFA 更加简洁, 适合用来描述语言 $L(\mathcal A)$

DFA 更加易于判断 $x\in L(\mathcal A)$, 适合产生词法分析器

所以我们的思路是: 用 NFA 描述语言, 用 DFA 实现词法分析器, $i.e.$

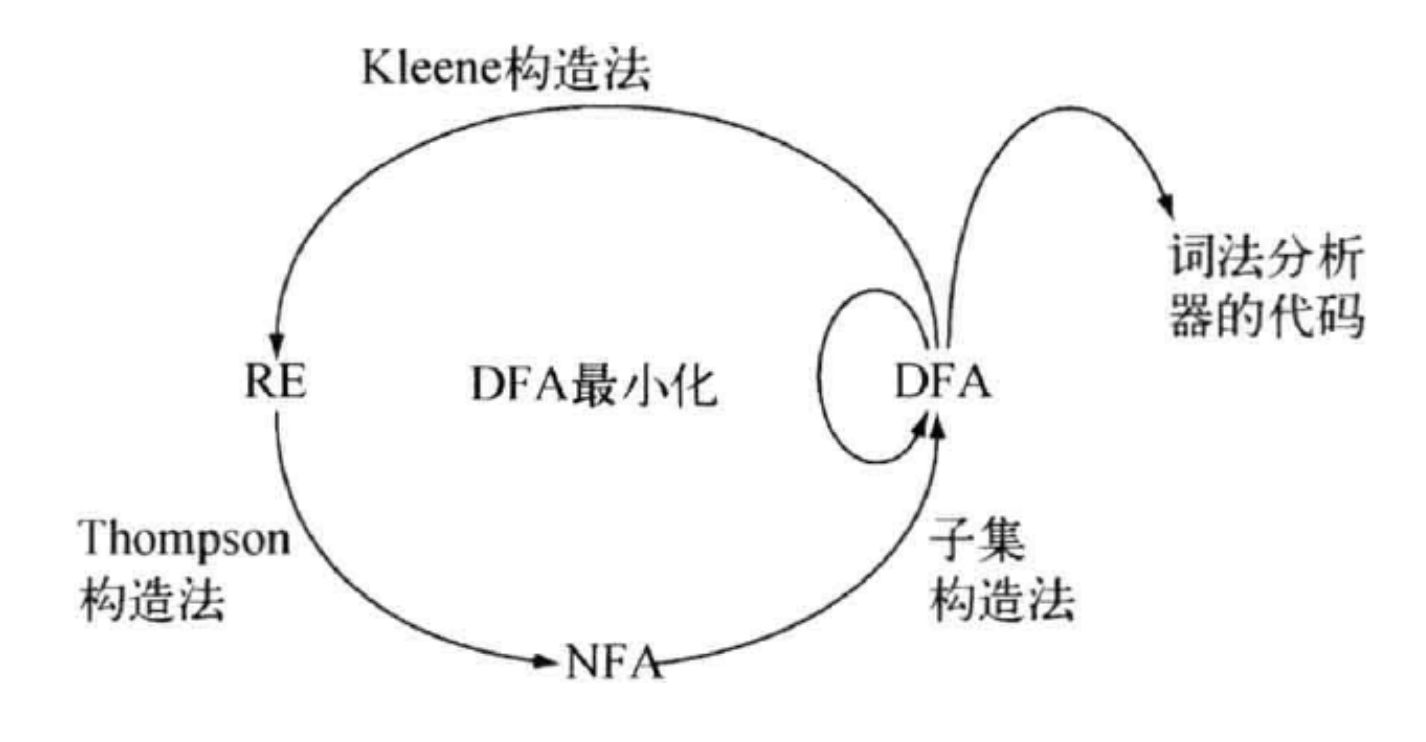
$$\text{RE}\Rightarrow \text{NFA} \Rightarrow \text{DFA} \Rightarrow \text{Lexer} $$

4.2. $\small \text{RE} \Rightarrow \text{NFA}:$ Thompson 构造法

即对于给定的正则表达式 $r$, 要将其转化为对应的 NFA $N(r)$, 且满足 $L(r)=L(N(r))$

Thompson构造法的基本思想

Thompson构造法的基本思想是: 按照结构归纳

根据上面给出的正则表达式的形式化定义, 将 NFA 的规则分成基本规则和归纳规则两种, 基本规则处理不包含运算符的子表达式, 归纳规则根据一个给定表达式的直接子表达式的 NFA 构造出这个表达式的 NFA

$(1)$ 基本规则 —— $\epsilon$ 是正则表达式:

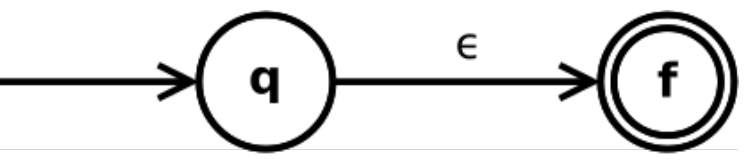
$(2)$ 基本规则 —— $\forall a\in \Sigma$, $a$ 是正则表达式:

$(3)$ 基本规则 —— 如果 $r$ 是正则表达式, 则 $(r)$ 也是正则表达式:

$$N((r))=N(r) $$

$(4)$ 归纳假设 —— 如果 $r$ 与 $s$ 是正则表达式, 则 $r|s$, $rs$, $r^*$ 也是正则表达式:

这里设计了$\epsilon$ 转移

一种扩展的NFA是NFA-λ（也叫做NFA-ε或有ε移动的NFA），它允许到新状态的变换不消耗任何输入符号。例如，如果它处于状态1，下一个输入符号是a，它可以移动到状态2而不消耗任何输入符号，因此就有了歧义：在消耗字母a之前系统是处于状态1还是状态2呢?由于这种歧义性，可以更加方便的谈论系统可以处在的可能状态的集合。因此在消耗字母a之前，NFA-ε可以处于集合{1,2}内的状态中的任何一个。等价的说，你可以想象这个NFA同时处于状态1和状态2:这给出了对幂集构造的非正式提示：等价于这个NFA的DFA被定义为此时处于状态q={1,2}中。不消耗输入符号的到新状态的变换叫做λ转移或ε转移。它们通常标记着希腊字母λ或ε。

我们首先假设正则表达式 $r$ 与 $s$ 的 NFA 分别为 $N(r)$ 和 $N(s)$, 那么根据假设, 它们必须满足 NFA 的递归定义.

$(4.1)$ 如果 $r$ 与 $s$ 是正则表达式, 则 $r|s$ 也是正则表达式:

r|s

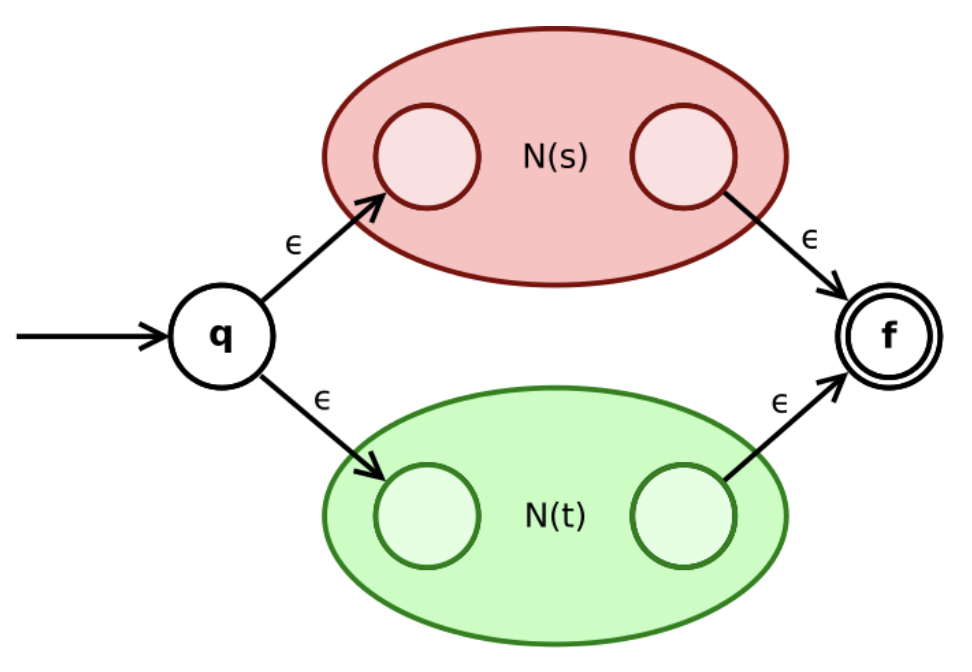
$(4.2)$ 如果 $r$ 与 $s$ 是正则表达式, 则 $rs$ 也是正则表达式:

rs

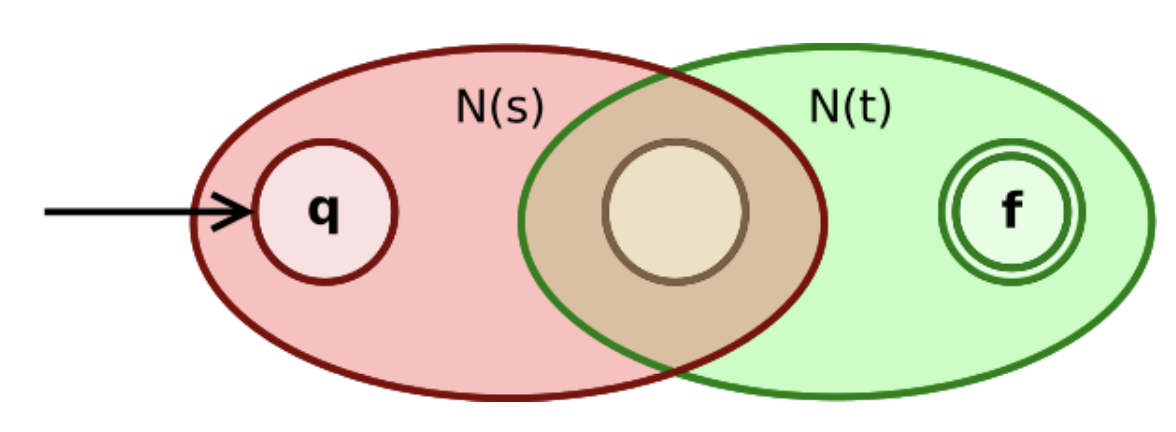
$(4.3)$ 如果 $r$ 与 $s$ 是正则表达式, 则 $r^*$ 也是正则表达式:

r*

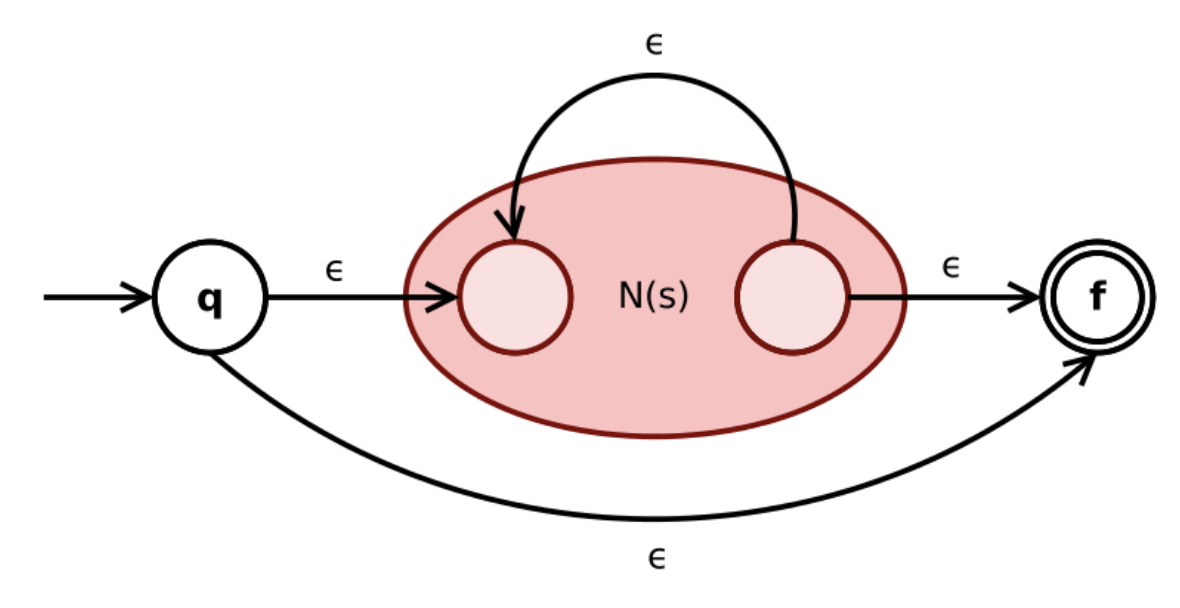
下面给出一个完整的例子. 对于正则表达式 $r=(a|b)^*abb$, 可以根据 Thompson构造法进行这样的构造

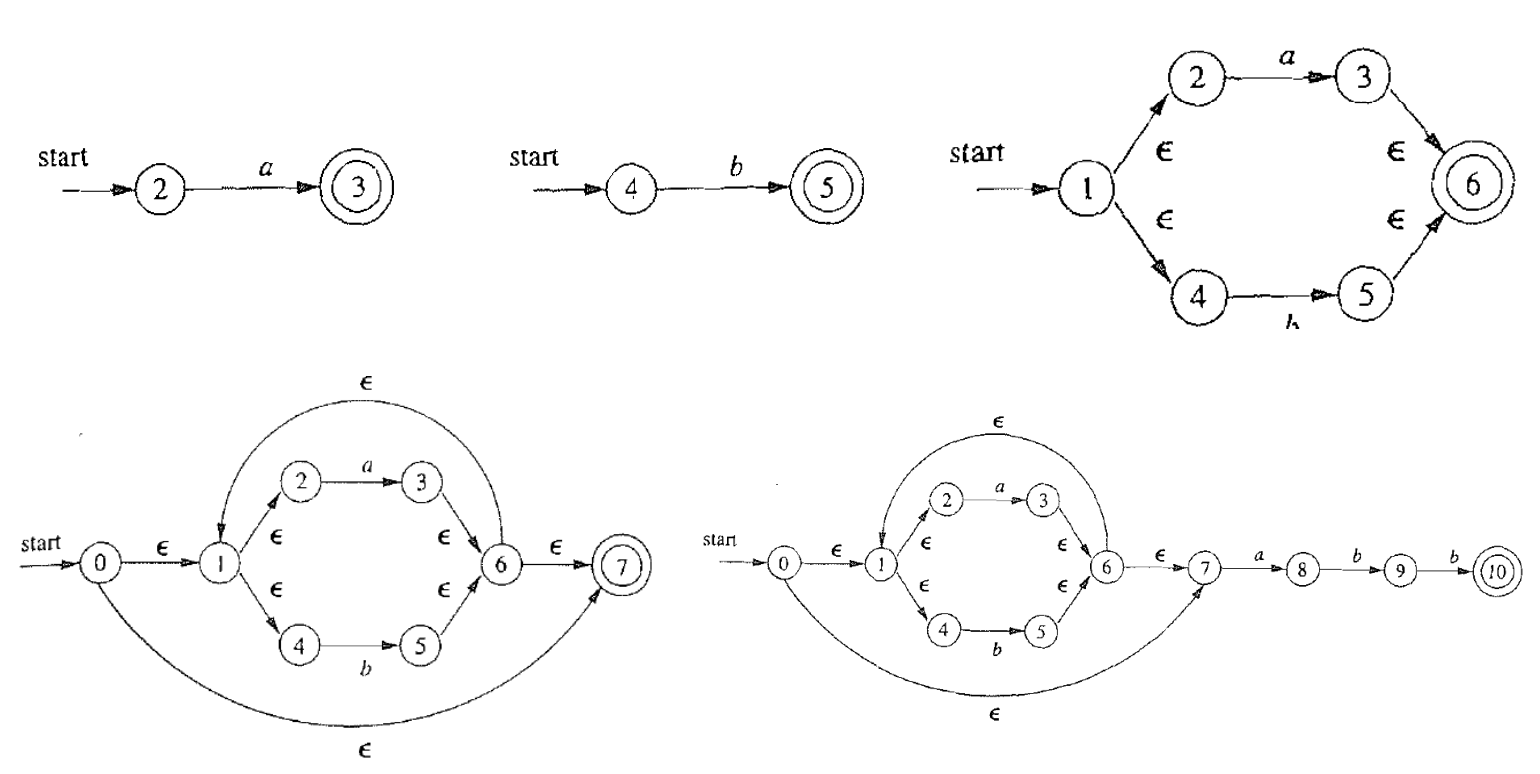
$N(r)$ 的性质和 Thompson 构造法的复杂度分析

  1. $N(r)$ 的开始状态和结束状态均唯一
  2. $N(r)$ 的开始状态没有入边, 结束状态没有出边
  3. $N(r)$ 的状态数 $|S|\leq 2\times |r|$ (其中 $|r|$ 为 $r$ 中运算符和运算分量的总和)
  4. 每个状态最多有两个 $\epsilon$-入边和两个 $\epsilon$-出边
  5. $\forall a\in \Sigma$, 每个状态最多有一个 $a$-入边和 $a$-出边

4.3. $\small \text{NFA} \Rightarrow \text{DFA}:$ 子集构造法

子集构造法的整体思想是, 用 DFA 模拟 NFA.

下面给出一个用 $\text{DFA}$ 来模拟 $\text{NFA}$ 的例子. 对于左边的 $\text{NFA}$, 可以使用如右图的 $\text{DFA}$ 来模拟.

$$L(\mathcal A) = L((a|b)^* abb) $$
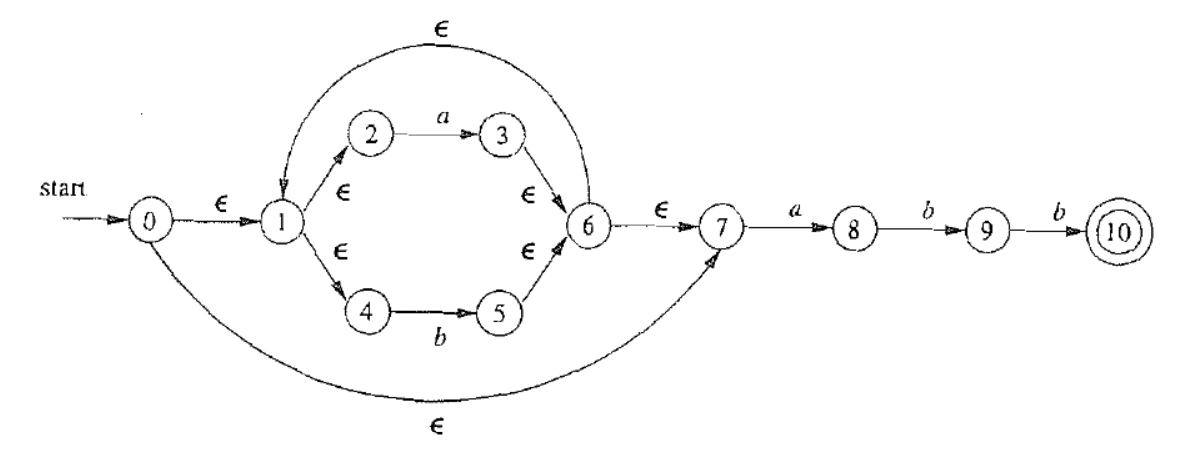
image-20230622165125946
NFA
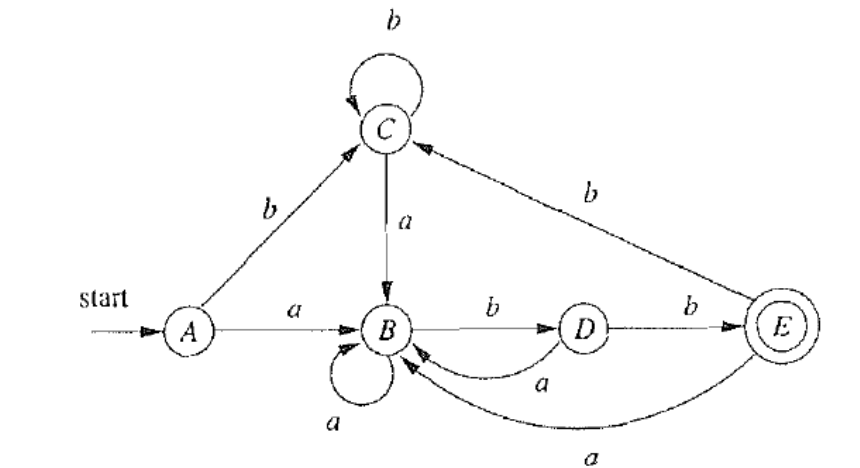
image-20230622165144361
DFA

并且其关键步骤给出如下:

为了展示子集构造法, 我们必须先阐述几个定义

$\epsilon\text{-closure}(s)$: 也就是状态 $s$ 的 $\epsilon\text{-}$闭包, 是只通过 $\epsilon\text{-}$转移就可达的状态集合. 形式化地定义如下:

$$\epsilon\text{-closure}(s) :=\{t \in S_N |s \stackrel {\large\epsilon^*}{\to} t\} $$

其中, 形式化地, 闭包 $f\text{-closure}(T)$ 的代数含义如下:

$$f\text{-closure}(T):=\{ x: x\in T \land f(x)=x\} $$

称为函数 $f$ 在 $T$ 上的闭包. 在此基础上, 再提出状态集的 $\epsilon\text{-}$闭包和状态集的转移函数的概念. 形式化地定义如下:

$$\epsilon\text{-closure}(T) :=\bigcup_{s\in T}\epsilon\text{-closure}(s) $$
$$\text{move}(T,a):=\bigcup_{s\in T}\delta(s, a) $$

在此基础上, 我们给出子集构造法的形式化表述.:

如果 $\text{NFA}$ $N$ 和 $\text{DFA}$ $D$ 的形式化定义如下:

$$N=(\Sigma_N, S_N, n_0, \delta_N, F_N) $$
$$D=(\Sigma_D, S_D, d_0, \delta_D, F_D) $$

一些比较关键的关系如下

  1. $\Sigma_D = \Sigma_N$

  2. $\forall s_D\in S_D:s_D\subseteq S_N$, 也就是说:

$$S_D\subseteq 2^{S_N} $$
  1. 初始状态 $d_0=\epsilon\text{-closure}(n_0)$
  2. 转移函数 $\forall a\in \Sigma_D:\delta_D(s_D,a)=\epsilon\text{-closure}(\text{move}(s_D, a))$
  3. 接受状态集 $F_D=\{s_D\in S_D|\exists f\in F_N:f\in s_D\}$

子集构造法的复杂度分析:

$(|S_N | = n)$

$ |S_D| = \text{Θ}(2^n )$

最坏情况下, $|S_D| = Ω(2^n )$

4.4. $\small \text{NFA} \Rightarrow \text{DFA}:\text{DFA}$ 最小化

上个阶段构建出来的 DFA 也确实已经是能拿来使用了. 但是不够简介. 我们将继续完善我们的 DFA, 来使它成为一个最简洁的 DFA. 最小化 DFA 的基本思想是: 划分而非合并 (合并在理论上只是下面这个逻辑式取反而已, 但是在计算上更加复杂.)

$$s \not \sim t \iff \exists a ∈ \Sigma: (s \stackrel {a}{\to} s') ∧ (t \stackrel {a}{\to}t') ∧ (s'\not \sim t') $$

$def:$ 如果分别从 $s$ 与 $t$ 出发, 沿着标号为 $x$ 的路径到达的两个状态中只有一 个是接受状态, 则称 $x$ 区分了状态 $s$ 与 $t$.

$def:$ 如果存在某个能区分状态 $s$ 与 $t$ 的字符串, 则称 $s$ 与 $t$ 是可区分的.

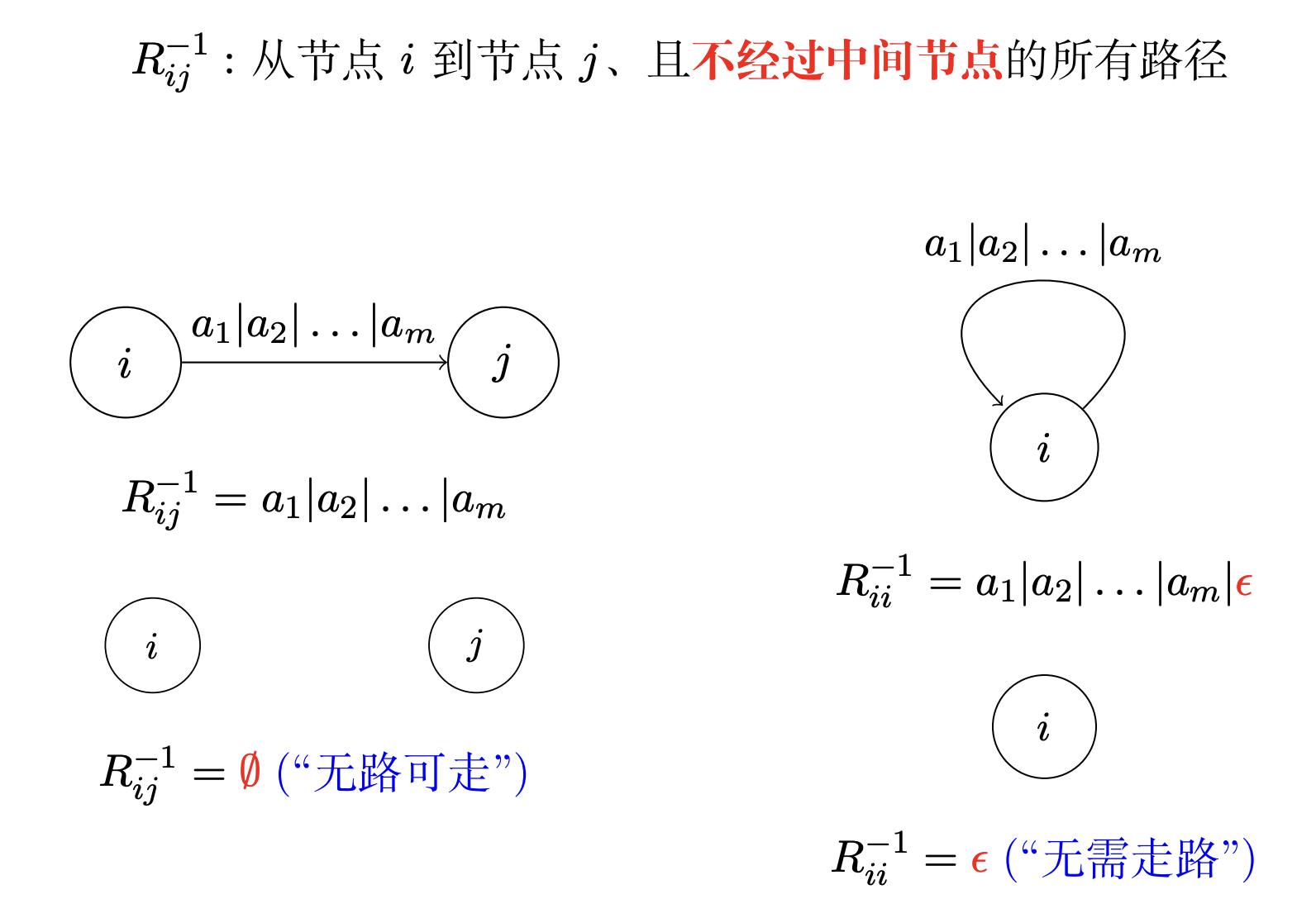
4.5. $\small \text{DFA} \Rightarrow \text{RE}$

没错我懒得打了

image-20230713225517722