Inductive Synthesis

CS › Program Synthesis

参考 MIT CS 6.S981 Lec 2

1. Intro to Inductive Synthesis

归纳合成 (Inductive Synthesis) 中的目标是生成与给定的一组输入/输出示例相匹配的函数. 包括两类:

  • Programming by Example (PBE): infer a function given only a set of inputs and outputs
  • Programming by Demonstration (PBD): the user also provides a trace of how the output was computed.

一般来说 PBD 包含有更多的信息, 但是两者的界限实际上很模糊.

试图实现 PBD 涉及到的两项关键的技术是:

  • Version Space Generalization
  • Inductive Logic Programming

which will be covered later.

2. PBD/PBE

在 PBE/PBD 范式中存在两个核心挑战:

  • 如何找到与观察结果相匹配的程序？
  • 如何知道找到的程序是用户真正想要的程序？

传统的机器学习由于选择了 extremely expressive 的 program space (e.g. Neural Network), 所以往往主要考虑第二个问题. 现代的 PBE 关注程序空间本身.

3. Programs

3.1. What is Program

A program is a description of how to perform a computation.

在另一个极端, 数字与四则运算也可以算作是一个编程语言. 在后面的课程中我们会看到, 选择合适的符号对于程序合成的成功至关重要. 相对于 C 和 Python 这样的高级语言, 我们往往选择领域特定语言 (DSL) 来进行合成, 因为方便.

3.2. Representing a Program

在编程时, 我们往往用文本来表示一个程序. 但是在合成时间, 我们希望用一个数据结构来表示程序. 这样的抽象数据结构可以忽略掉一些不重要的东西 (比如 ;). As an example, consider the language of arithmetic expressions. The syntax of such a language can be represented as a context free grammar.

1
2
3
4
5
expr := term |
        term + expr
term := (expr) | 
        term * term
        N

CFG 捕捉了很多语法 (syntactic) 信息, 比如优先计算 *, 但是我们在 AST 中并不需要知道这样的信息 (品一下.), 所以我们可以忽略掉一些 syntactic 信息. 比如下面就是一个刻画了 AST 信息的 Haskell 表示.

1
2
3
data AST = Num Int
        | Plus AST AST
        | Times AST AST

4. Search

在任何程序合成问题中都无法回避搜索. 我们在这里探究几个基本的问题:

  • 程序空间是什么 (在什么里搜索)
  • 有哪些常见的搜索技术.

4.1. Program Space

一般来说, 程序合成问题中的程序空间指的是 一个小型领域特定语言 内所有可能的程序, 通过 AST 的形式来刻画, 而 AST 我们可以用 CFG 来描述. 这样做的前提是这个语言足够简单, 我们仅仅用 CFG 就可以枚举出这个语言的所有程序.

考虑这样一种语言

1
2
3
4
5
6
7
8
9
10
lstExpr := sort(lstExpr)
         | lstExpr[intExpr, intExpr] # sublist
         | lstExpr + lstExpr # concat 
         | recursive(lstExpr)
         | [0]
         | in   # the input list
intExpr := firstZero(lstExpr)
         | len(lstExpr)
         | 0
         | intExpr + 1

上面的语言包含有两种表达式: list 和 int. 实际上这一语言的表达能力很强, 比如下面是一个用来 inverse list 的例子

1
recursive(in[0 + 1, len(in)]) + in[0, 0]

在另一方面我们的 DSL 又是如此的合适, 因为如果用 Python 或者 C 这样的高级语言来合成的话, 将会有非常多种程序. 但是实际上我们的 DSL 能合成的最短的(满足要求的)程序, 正是上面的程序. 这个例子说明了程序空间的选择是非常重要的.

常见的搜索技术分成两类:

  • Explicit Enumeration
  • Symbolic search

4.2. Explicit Enumeration

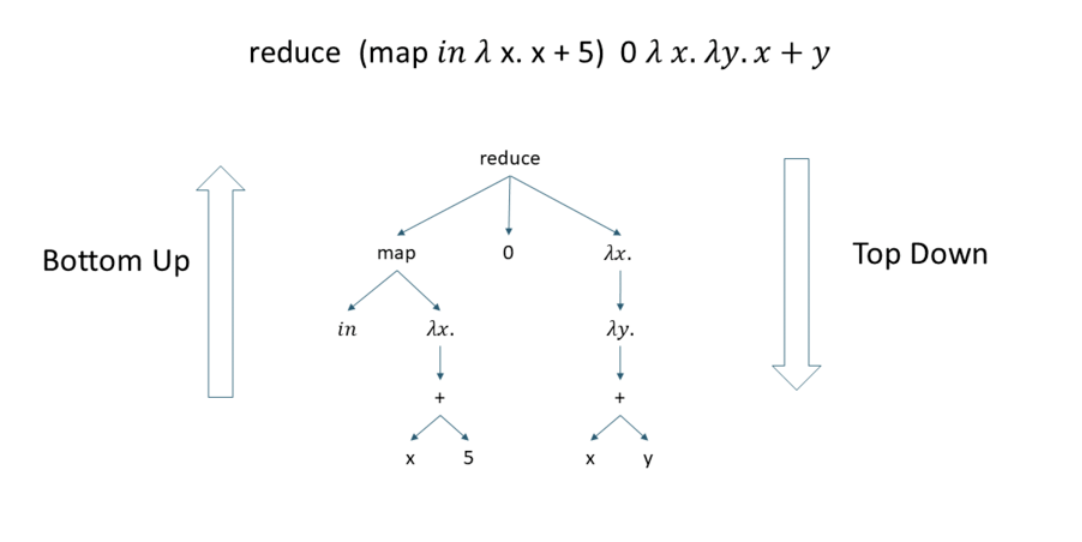
一般来说程序空间都是无限大的, explicit enumeration 的主要任务找到一个合适的枚举顺序, 使得程序可以较快地被枚举出来. 基于这样的想法, enumeration 又分成两类:

  • top-down
  • bottom-up

在显式搜索中，Synthesizer 始终维护一个或多个 当前正在考虑的部分 构造程序. 相比之下在 Symbolic Search 中, Synthesizer 维护 所有被认为有效的程序空间的符号表示. 不同的符号表示会导致不同的搜索算法. 当今使用最广泛的两种符号表示:

  • Version Space Algebras.
  • Constraint System.

但现实是 symbolic search 太困难, 以至于在大部分常见的场景下, 都是 explicit enumeration 的效果更好.