9. High-dimensional Data

$$\huge\textbf{High-dimensional Data}$$

1. Dimensionality

1.1. Curse of Dimensionality

纬度灾难 (Curse of dimensionality) 最早由美国应用数学家理查德·贝尔曼在考虑优化问题时首次提出来, 用来描述当 (数学) 空间维度增加时, 分析和组织高维空间 (通常有成百上千维), 因体积指数增加而遇到各种问题场景. 这样的难题在低维空间中不会遇到, 如物理空间通常只用三维来建模.

1.2. $\text{Gauss}$ Ring Theorem

一个均值为 $0$，方差为 $\sigma^2$ 的 $d$ 维 $\text{Gauss}$ 分布的密度函数为：

$$p(x) = \frac{1}{(2\pi)^{\frac{d}{2} }\sigma^d}\exp(-\frac{||x||^2}{2\sigma^2})$$

$def$: $\text{Gauss}$ 环定理

在任意方向上都有单位方差的 $d$ 维球面 $\text{Gauss}$ 分布，$\forall\beta\leq\sqrt d$，除了最多 $3e^{-c\beta^2}$ 的概率质量外，其余质量都在

$$\sqrt d -\beta \leq||x||\leq \sqrt d + \beta$$

的环里, 其中 $c$ 为正常数.

1.3. $\text{J-L}$ Lemma

$\text{Johnson-Lindenstrauss} \ Lemma$ 与1984年由 $\text{William Johnson}$ 和 $\text{Joram Lindenstrauss}$ 提出.

$lemma.$ $\text{J-L}$ 引理

对给定的 $\varepsilon \in (0,1)$ 以及 $N$ 维 $\text{Euclidian}$ 空间的 $m$ 个点 $\{x_1, x_2, …,x_n\}$，对于任意满足条件的 $n\in \mathbb N$ 且 $n > \frac{lnm}{ {\varepsilon^2\over 2} - {\varepsilon^3\over 3} }$，存在一个线性映射 $f:\mathbb{R}^N\to\mathbb{R}^n$，将这 $m$ 个点，从 $\mathbb{R}^N$ 中映射到 $\mathbb{R}^n$，同时“基本上”保持了点集成员两两之间的距离，即：

$$\forall x_i,x_j:(1-\varepsilon)||x_i-x_j||^2_2\leq ||f(x_i)-f(x_j)||^2_2\leq (1+\varepsilon)||x_i-x_j||^2_2\quad(1\leq i<j\leq m)$$

更进一步地，这个线性映射 $f$ 还可以在多项式时间内给出.

2. Correlation Analysis

2.1. $\text{Pearson}$ Correlation Coefficient

$def.$ $\text{Pearson}$ 相关系数（$\text{Pearson}$-$r$）

两个**样本** (注意不是总体) $X,Y$ 的 $\text{Pearson}$ 相关系数可以用来描述两个统计样本之间的线性关系（当然也可能存在良好的非线性关系使得该系数为 0），是两个容量为 $n$ 的样本值的标准偏差之积的累加和除以自由度 $n-1$，即

$$r_{XY}:=\frac{1}{n-1}\sum_{i=1}^n(\frac{X_i-\overline X}{s_X})(\frac{Y_i-\overline Y}{s_Y})$$

$thm.$ Pearson-$r$ 计算公式

$$r_{XY}=\frac{n\displaystyle\sum_iX_iY_i-\displaystyle\sum_iX_i\displaystyle\sum_iY_i}{\sqrt {n\displaystyle\sum_iX_i^2-(\displaystyle\sum_iX_i)^2}\sqrt { {n\displaystyle\sum_iY_i}-(\displaystyle\sum_iY_i)^2} }$$

关于 $\text{Pearson}$ 相关系数的更具体的介绍, 可以查看我的这篇文章

3. Dimensionality Reduction

3.1. Introduction

研究表明, 当维数越来越多时, 分析和处理多维数据的复杂度和成本成指数级增长; 与此同时, 在分析高维数据时, 所需的空间样本数会随维数的增加成指数增长. 数据降维的应用很多, 比方说特征工程

3.2. Principal Components Analysis, PCA

1. Principles

$def.$ 主成分分析

主成分分析 (Principal Components Analysis, PCA) 由 Pearson ^[1] 于 1901 年提出. 主成分分析是一种简单的非参数的统计分析⽅法, 用于从混乱的数据集中提取相关信息, 进行**数据降维**. 它可以将多个相关变量转化为少数⼏个不相关变量. 通过主成分分析 PCA 量保留原始信息, 并在此基础上尽可能提出更少的不相关变量 (主成分), 可以对数据进⾏有效的降维. 下图是 PCA 的投影的⼀个表⽰, 蓝⾊的点是原始的点, 带箭头的橘⻩⾊的线是投影的向量, 表⽰特征值最⼤的特征向量, 表⽰特征值次⼤的特征向量.

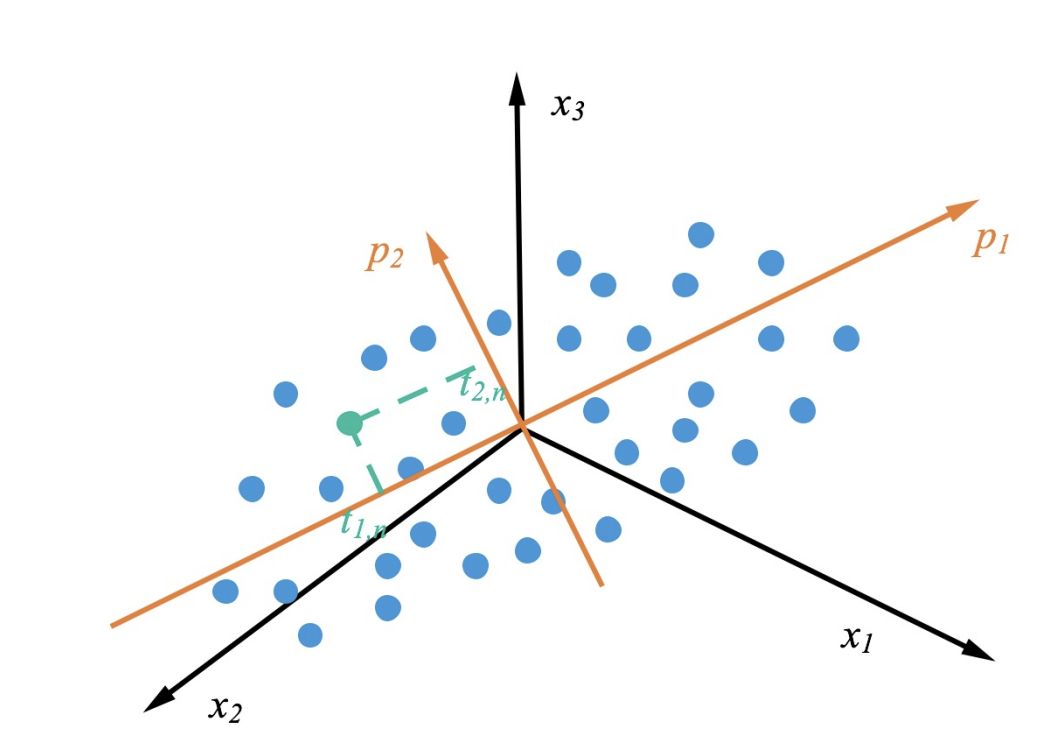
2. Steps

设有随机变量 $X_1,X_2,…,X_p$, 样本标准差记为 $S_1,S_2,…,S_p$. 首先做标准化变换:

$$C_j = \sum_{i = 1}^pa_{ji}x_i\ (j = 1,2,…,p)$$

注意, 标准化的⽬的是为了让数据的均值为 0, 标准差为 1.

$def.$ 第一主成分

若 $C_1 = \displaystyle\sum_{i = 1}^pa_{1j}x_j$，且使 $Var(C_1)$ 最大，则称 $C_1$ 为第一主成分.

$def.$ 第二主成分

若 $C_2 = \displaystyle\sum_{i = 1}^pa_{2j}x_j$，$(a_{21},a_{22},…,a_{2p})$ 与 $(a_{11},a_{12},…,a_{1p})$ 垂直且使 $Var(C_2)$ 次大, 则称 $C_2$ 为第二主成分.

类似地定义下去, 可以有第三, 第四, …主成分. 至多有 $p$ 个. $p$ 的取值由人来决定, 和随机变量的数目有关, 也与实际应用有关.

更加通俗地从矩阵的角度来考虑, PCA 可以理解为将⼀个 $m$ 维的数据转换称⼀个 $k$ 维的数据, 其中 $k<m$. 对于具有 $n$ 个样本的数据集, 假设 $\boldsymbol{x}_{i}$ 表⽰ $m$ 维的列向量, 则

$$X_{m * n}=\left(\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \ldots, \boldsymbol{x}_{n}\right)$$

对每⼀个维度进⾏零均值化，即减去这⼀维度的均值

$$X_{m * n}^{\prime}=X-\boldsymbol{u h}$$

其中, $\boldsymbol{u}$ 是⼀个 $m$ 维的⾏向量, $\boldsymbol{u}[m]=\displaystyle\frac{1}{n} \sum_{i=1}^{n} X[m, i]$; $h$ 是⼀个值全为 1 的 $n$ 维⾏向量. 对于已经零均值化的矩阵 $X'$, 有:

$$C=\frac{1}{n} X^{\prime} X^{\prime \mathsf T}=\left(\begin{array}{cccc} \displaystyle\frac{1}{n} \sum_{i=1}^{n} x_{1 i}^{2} & \displaystyle\frac{1}{n} \sum_{i=1}^{n} x_{1 i} x_{2 i} & \cdots & \displaystyle\frac{1}{n} \sum x_{1 i} x_{n i} \\ \displaystyle\frac{1}{n} \sum_{i=1}^{n} x_{2 i} x_{1 i} & \displaystyle\frac{1}{n} \sum_{i=1}^{n} x_{2 i}^{2} & \cdots & \displaystyle\frac{1}{n} \sum x_{2 i} x_{n i} \\ \vdots & \vdots & \vdots \\ \displaystyle\frac{1}{n} \sum_{i=1}^{n} x_{m i} x_{1 i} & \displaystyle\frac{1}{n} \sum_{i=1}^{n} x_{m i} x_{2 i} & \cdots & \displaystyle \frac{1}{n} \sum x_{m i}^{2}\end{array}\right)$$

因为矩阵 $X'$ 已经经过了零均值化处理, 因此矩阵 $C$ 中对⻆线上的元素为维度 $m$ 的⽅差, 其他元素则为两个维度之间的协⽅差. 从 PCA 的⽬标来看, 我们则可以通过求解矩阵 $C$ 的特征值和特征向量, 将其特征值按照从⼤到小的顺序按⾏重排其对应的特征向量, 则取前 $k$ 个, 则实现了数据从 $m$ 维降⾄ $k$ 维.

3. Properties

值得注意的是, 主成分分析后得到的向量与原向量之间有一些关系:

1. 各成分间互不相关, 即

$$\operatorname{Corr}(C_i,C_j) = 0\ (i\not = j)$$

2. 组合系数构成的向量 $(a_{i1},a_{i2},…,a_{ip})$ 为单位向量

3. 主成分的方差是依次递减的, 即

$$V(C_1)\geq V(C_2)\geq …\geq V(C_p)$$

4. 总方差不增不减 (主成分只是原变量的线性组合), 即

$$\sum_{i = 1}^pV(C_i)=\sum_{i=1}^pV(x_i)=p$$

5. 主成分与原变量的相关系数满足

$$\operatorname {Corr}(C_i,x_j) = a_{ij}$$

6. 令 $X_1,X_2,…,X_p$ 的相关矩阵为 $R$，$(a_{i1},a_{i2}.…,a_{ip})$ 则是相关矩阵 $R$ 的第 $i$ 个特征向量。且特征值 $l_i$ 就是第 $i$ 主成分的方差

3.3. Linear Discriminant Analysis, LDA

1. Principles

判别分析是一种统计技术, 其中线性判别分析 (Linear Discriminant Analysis) 是对 $\text{Fisher}$ 线性鉴别方法的归纳.

$def.$ 线性判别分析

线性判别分析是一种找到最佳分离两个或者多个类的变量的线性组合的方法. 该方法思想比较简单: 给定训练集样例, 设法将样例投影到一维的直线上, 使得同类样例的投影点尽可能接近和密集, 异类投影点尽可能远离. 不过 LDA 的逻辑基于如下的两个假设:

• 原始数据根据样本均值进行分类.
• 不同类的数据拥有相同的协方差矩阵.

当然在实际情况中, 不可能满足以上两个假设. 但是当数据主要是由均值来区分的时候, LDA一般都可以取得很好的效果.

2. Steps

更加具体地说, 为了使得类别内的点距离越近越好, 类别间的点越远越好, 我们刻画了两个变量 $S_{W(ithin)}$ 和 $S_{B(etween)}$:

$$\begin {align} S_{W}&=\sum_{\text {classes }c} \sum_{j\in c} p_{c}\left(\boldsymbol {x}_{j}-\boldsymbol{\mu}_{c}\right)\left(\boldsymbol {x}_{j}-\boldsymbol{\mu}_{c}\right)^{\mathsf T}\\ S_B&=\sum_{\text{classes }c}(\boldsymbol \mu_c-\boldsymbol \mu)(\boldsymbol \mu_c-\boldsymbol \mu)^{\mathsf T} \end {align}$$

众所周知向量内积有投影的效果 (我们先不考虑大小), 那我们考虑找到这样的一个最合适的 $\boldsymbol w$ (的方向) 来进行投影. 令 $y=\boldsymbol w^{\mathsf T}\boldsymbol x$, 则

$$\begin {align} \boldsymbol w^{\mathsf T}S_{W}\boldsymbol w&=\sum_{\text {classes }c} \sum_{j\in c} p_{c}(\boldsymbol w^{\mathsf T}\left(\boldsymbol {x}_{j}-\boldsymbol{\mu}_{c}\right))(\boldsymbol w^{\mathsf T}\left(\boldsymbol {x}_{j}-\boldsymbol{\mu}_{c}\right))^{\mathsf T}\\ \boldsymbol w^{\mathsf T}S_{B}\boldsymbol w&=\sum_{\text{classes }c}(\boldsymbol w^{\mathsf T}(\boldsymbol \mu_c-\boldsymbol \mu))(\boldsymbol w^{\mathsf T}(\boldsymbol \mu_c-\boldsymbol \mu))^{\mathsf T} \end {align}$$

我们考虑使

$$f(\boldsymbol w)=\frac{\boldsymbol w^{\mathsf T}S_{W}\boldsymbol w}{\boldsymbol w^{\mathsf T}S_{B}\boldsymbol w}$$

最小 (这样的设计也消除了量纲的影响, 这也是为什么上面先不考虑大小). 很自然地我们考虑

$$\begin{align} \frac{\mathrm df}{\mathrm d\boldsymbol w}&=\frac{S_{B} \boldsymbol w\left(\boldsymbol w^{\mathsf T} S_{W} \boldsymbol w\right)-S_{W} \boldsymbol w\left(\boldsymbol w^{\mathsf T} S_{B} \boldsymbol w\right)}{\left(\boldsymbol w^{\mathsf T} S_{W} \boldsymbol w\right)^{2}}=0 \\ &\implies S_{W} \boldsymbol w=\frac{\boldsymbol w^{\mathsf T} S_{W} \boldsymbol w}{\boldsymbol w^{\mathsf T} S_{B} \boldsymbol w} S_{B} \boldsymbol w=f(\boldsymbol w) S_{B} \boldsymbol w\propto S_B\boldsymbol w\end{align}$$

显然 $S_W^{-1}S_B$ 的特征值就是 $f(\boldsymbol w)$, 特征向量就是 $\boldsymbol w$.

总的来说, LDA 的算法包括如下的几个步骤:

• 计算每个类别的均值 $\boldsymbol \mu_i$, 全局样本均值 $\boldsymbol \mu$
• 计算类内散度矩阵 $S_W$, 类间散度矩阵 $S_B$
• 对矩阵 $S_W^{-1}S_B$ 做特征值分解
• 取最大的数个特征值所对应的特征向量
• 计算投影矩阵

3.4. Locally Linear Embedding, LLE

1. Principles

$def.$ 局部线性嵌入

局部线性嵌入 (Locally Linear Embedding, LLE) 方法基于这样的假设: 靠的足够近的数据之间近似是线性的. LLE的基本想法是, 努力去保留相邻数据间的关系, 数据集中的数据用其局部近邻线性近似. 在效果上, LLE 消除了估计广泛分析的数据点之间成对距离的需要, 从局部线性拟合中恢复全局非线性结构.

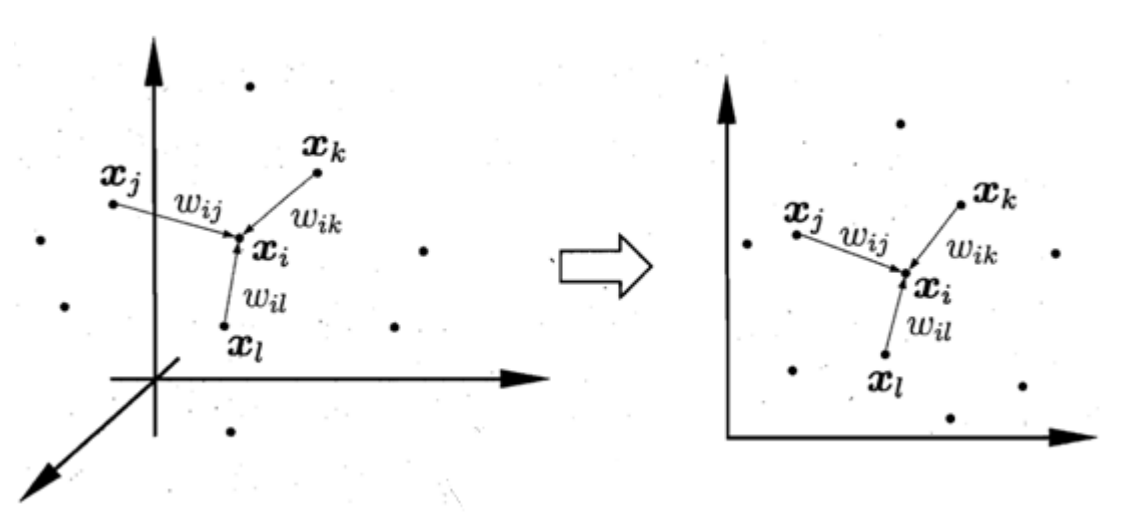
一般来说, 确定一个点是不是当前点的临近点有两种方法:

• 距离: 和当前点的距离小于预先定义的距离 $d$ 的点集合
• 个数: 前 $k$ 个靠得最近的点集合

为了方便调节, 我们用一个权重矩阵 $W$ 来为数据集 (大小为 $n$ ) 中的所有点对之间的距离刻画权重. 假设 $Q(i)$ 表示距离 $\boldsymbol x_i$ 前 $k$ 近的 $k$ 个点的 index

$$\forall i: \sum_{j\in Q(i)}W_{ij}=1\tag{1}$$

如果点 $\boldsymbol x_j$ 距离当前点 $\boldsymbol x_i$ 很远, 那么记 $W_{ij}=0$, 记残差函数

$$\varepsilon=\sum_{i=1}^{n}\|\boldsymbol x_i-(\sum_{j=1}^n W_{ij}\boldsymbol x_j)\|^2$$

我们考虑将 $\varepsilon$ 矩阵化.

$$\begin{align} \varepsilon&=J(W)\\ &=\sum_{i=1}^{n}\|(\sum_{j\in Q(i)} W_{ij}\boldsymbol x_i)-(\sum_{j\in Q(i)} W_{ij}\boldsymbol x_j)\|^2\\ &=\sum_{i=1}^{n}\sum_{j\in Q(i)}\|W_{ij}\boldsymbol x_i- W_{ij}\boldsymbol x_j\|^2\\ &=\sum_{i=1}^{n}\boldsymbol W_{i}^{\mathsf T}(\boldsymbol x_i-\boldsymbol x_j)(\boldsymbol x_i-\boldsymbol x_j)^{\mathsf T}\boldsymbol W_{i}\tag{2} \end {align}$$

我们令 $Z=(\boldsymbol x_i-\boldsymbol x_j)(\boldsymbol x_i-\boldsymbol x_j)^{\mathsf T}$, 这时我们可以将 (1) 和 (2) 使用 $\text{Lagrange}$ 乘数法共同写成同一个优化函数. 假设 $\boldsymbol \alpha=(1,1,...,1)^{\mathsf T}$

$$L(W)=\sum_{i=1}^{n}\boldsymbol W_{i}^{\mathsf T}Z\boldsymbol W_{i}\tag{2}+\lambda(\boldsymbol W_i^{\mathsf T}\boldsymbol \alpha-1)$$

我们对 $W$ 求偏导,

$$\begin{align} \frac{\partial L}{\partial W}=0&\implies 2\boldsymbol Z_i\boldsymbol W_i+\lambda\alpha=0\\ &\implies\boldsymbol W_i=\frac{\boldsymbol Z_i^{-1}\boldsymbol \alpha}{\boldsymbol \alpha^{\mathsf T}\boldsymbol Z_i^{-1}\boldsymbol \alpha} \end {align}$$

2. Calculation

3.5. $t\text{-}$distributed stochastic neighbor embedding, $t\text{-}$SNE

$def.$ $t\text-$分布邻域嵌入

$t$ 分布邻域嵌入 ($t\text{-}$distributed stochastic neighbor embedding, $t\text{-}$SNE）将数据点间的距离转化为概率分布并且以此来表达点与点之间的相似度，算法使得高低维数据分布尽可能接近为目标.

4. References

---

1. Pearson, Karl. LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 2.11 (1901): 559-572. ↩︎