CS►Machine Learning

Feature Engineering

“数据和特征决定了机器学习的上限, 而模型和算法只是逼近这个上限而已”. [1]

1. Intro

在现实⽣活中, 所有的事物都具有多种多样的属性 (Attribute). 在数据科学中, 我们将⼀个所考察的对象的属性集合称之为特征 (Feature) 或特征集. 特征⼯程 (Feature Engineering) 顾名思义是对特征进⾏⼀系列加⼯操作的过程, 对于特征⼯程有多种不同的定义：

  1. 特征⼯程是利⽤对数据的业务理解构建适合特定机器学习算法的特征的过程 [2].
  2. 特征⼯程是将原始数据转换成特征的过程。这些特征能够更好的将根本问题表达表述成预测模型, 同时利⽤不可直 接观测的数据提⾼模型准确性 [3].
  3. 特征⼯程就是⼈⼯设计模型的输⼊变量 $x$ 的过程 [4]
  4. …

从数据挖掘过程的⻆度, 对 “传统的” 特征⼯程给出如下定义. 特征⼯程就是指从原始数据 (即通过现实⽣活中的实际业务发⽣产⽣的数据) 加⼯得到最终⽤于特定的挖掘算法的输⼊变量的过程. 此处之所以强调是 “传统的” 特征⼯程主要是⽤于区分其和近期基于深度学习等⽅法的⾃动特征⽣成. 因此, 特征工程可以分为如下几个阶段:

  • Data Preprocessing (特征提取)
  • Feature transformation and encoding（特征变换和编码）
  • Feature extraction and selection（特征提取和选择）
  • Feature monitoring（特征监控）

2. Data Preprocessing

2.1. Why Missing

在实际的项⽬中, 数据从⽣产和收集过程中往往由于机器或⼈的问题导致脏数据的⽣成, 这些脏数据包括缺失, 噪声, 不⼀致等等⼀系列问题数据. 脏数据的产⽣是不可避免的, 但在后期的建模分析过程中, 如果直接使⽤原始数据进⾏建模分析, 则得到的结果会受到脏数据的影响从而表现很差.

$$\text{Data Cleaning}\to\text{Data Laundering}\to\text{Data Scrubbing}\to \text{Data Massaging} $$

2.2. Missing Data Processing

对于数据缺失的情况, Rubin [5] 从缺失机制的⻆度分为 3 类

  • 完全随机缺失 (missing completely at random, MCAR)
  • 随机缺失 (missing at random, MAR)
  • ⾮随机缺失 (missing not at random, MNAR)

在 Missing Data [6] 中定义有, 对于⼀个数据集, 变量 $Y$ 存在数据缺失, 如果 $Y$ 的缺失不依赖于 $Y$ 和数据集中其他的变量, 称之为 MCAR. 如果在控制其他变量的前提下, 变量 $Y$ 不依赖于 本⾝, 称之为 MAR, 即：

$$P\left(Y_{\text {missing }} \mid Y, X\right)=P\left(Y_{\text {missing }} \mid X\right) $$

如果上式不满⾜, 则称之为 MNAR.

至于 Missing Data Imputation, 直接从sklearn调包

2.3. Duplicates Removing

去重是指对于数据中重复的部分进⾏删除操作, 对于⼀个数据集, 可以从样本和特征两个⻆度去考虑重复的问题.

样本去重: 从“样本”的⻆度, 相同的事件或样本 (即所有特征的值均⼀致) 重复出现是可能发⽣的. 但从业务理解的⻆度上考虑, 并不是所有的情况都允许出现重复样本, 例如: 我们考察⼀个班级的学⽣其平时表现和最终考试成绩之间的相关性时, 假设利⽤学号作为学⽣的唯⼀标识, 则不可能存在两个学号完全相同的学⽣. 则这种情况下我们就需要对于重复的“样本”做出取舍.

特征去重：从“特征”的⻆度, 不同的特征在数值上有差异, 但其背后表达的物理含义可能是相同的. 例如: ⼀个⼈的⽉均收⼊和年收⼊两个特征, 尽管在数值上不同, 但其表达的都是⼀个⼈在⼀年内的收⼊能⼒, 两个特征仅相差常数倍. 因此, 对于仅相差常数倍的特征需要进⾏去重处理, 保留任意⼀个特征即可. 常量特征剔除: 对于常量或⽅差近似为零的特征, 其对于样本之间的区分度贡献为零或近似为零, 这些特征对于后⾯的建模分析没有任何意义.

2.4. Anomaly Processing

异常处理

异常值是指样本中存在的同样本整体差异较⼤的数据, 异常数据可以划分为两类:

  1. 异常值不属于该总体，而是从另⼀个总体错误抽样到样本中而导致的较⼤差异.
  2. 异常值属于该总体，是由于总体所固有的变异性而导致的较⼤差异。

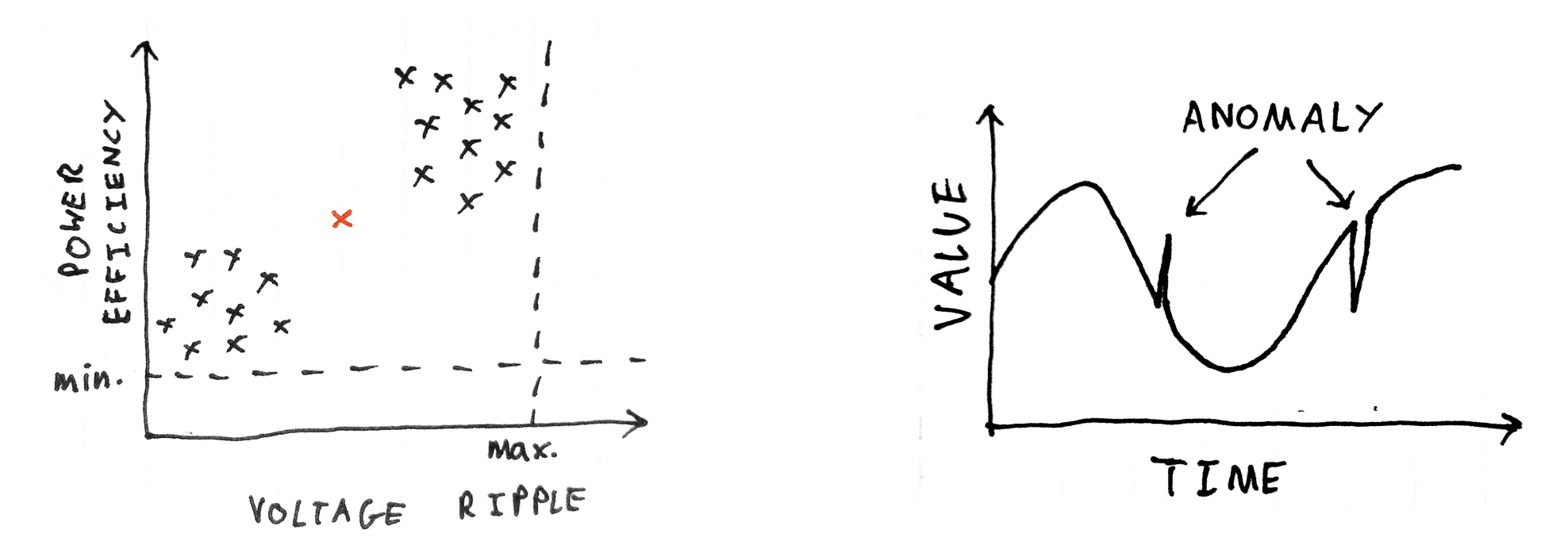
对于数值型的单变量, 我们可以利⽤拉依达准则对其异常值进⾏检测. 假设总体 $x$ 服从正态分布, 则:

$$P(|x-\mu|>3\sigma)\le 0.003 $$

其中 $\mu$ 表⽰总体的期望, 表⽰ $\sigma$ 总体的标准差. 因此, 对于样本中出现⼤于 $\mu+3\sigma$ 或小于 $\mu-3\sigma$ 的数据的概率是⾮常小的, 从而可予以剔除.

那么对于更加一般的单变量, 我们需要通过异常检测 (Anomaly Detection) 手段是指对不符合预期模式或数据集中异常项⽬、事件或观测值的识别. 通常异常的样本可能会导致银⾏欺诈、结构缺陷、医疗问题、⽂本错误等不同类型的问题. 异常也被称为离群值、噪声、偏差和例外.

常⽤的异常检测算法有:

  • 基于密度的⽅法: 最近邻居法、局部异常因⼦等 One-Class SVM
  • 基于聚类的⽅法
  • $\text{Isolation Forest}$
  • $\text{AutoEncoder}$

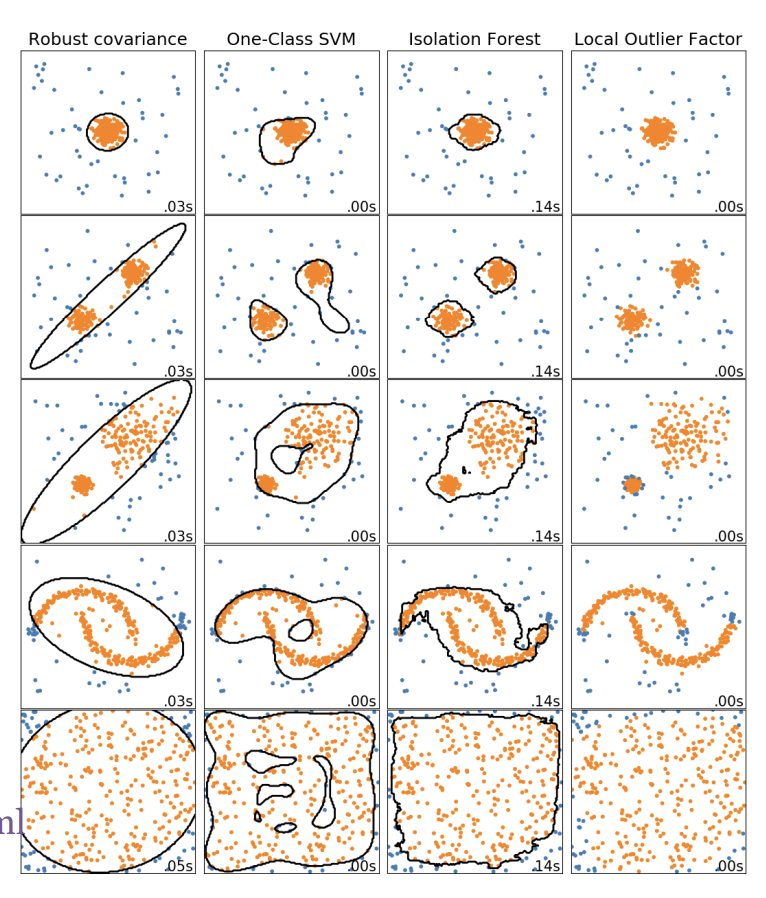
这里我们需要重点关注Isolation Forest.

Isolation Forest, 简称 $\text{iForest}$ [7][8]. $\text{iForest}$ 算法⽤于挖掘异常数据, 或者说离群点挖掘, 总之是在⼀⼤堆数据中, 找出与其它数据的规律不太符合的数据. 通常⽤于⽹络安全中的攻击检测和流量异常等分析, ⾦融机构则⽤于挖掘出欺诈⾏为. 对于找出的异常数据, 要么直接清除异常数据, 如数据清理中的去除噪声数据, 要么深⼊分析异常数据, ⽐如分析攻击、欺诈的⾏为特征.

$\text{iForest}$ 属于⾮监督学习的⽅法, 假设我们⽤⼀个随机超平⾯来切割数据空间, 切⼀次可以⽣成两个⼦空间. 之后我们再继续⽤⼀个随机超平⾯来切割每个⼦空间, 循环下去, 直到每⼦空间⾥⾯只有⼀个数据点为⽌. $\text{iForest}$ 由 $t$ 个 $\text{iTree}$ (Isolation Tree) 孤⽴树组成, 每个 $\text{iTree}$ 是⼀个⼆叉树结构, 其实现步骤如下:

  1. 从训练集中随机选择 $\phi$ 个点样本点, 放⼊树的根节点.
  2. 随机指定⼀个特征, 在当前节点数据中随机产⽣⼀个切割点 $p$, 切割点产⽣于当前节点数据中指定维度的最⼤值和最小值之间.
  3. 以此切割点⽣成了⼀个超平⾯, 将当前数据空间划分为 2 个⼦空间: 小于 $p$ 的数据作为当前节点的左孩⼦, ⼤于等于的数据作为当前节点的右孩⼦.
  4. 在孩⼦节点中递归步骤 2 和 3, 不断构造新的孩⼦节点, 直到孩⼦节点只有⼀个数据或孩⼦节点已到达限定⾼度.

获得 $t$ 个 $\text{iTree}$ 之后, $\text{iForest}$ 训练就结束, 然后我们可以⽤⽣成的 $\text{iForest}$ 来评估测试数据了. 对于⼀个训练数据, 我们令其遍历每⼀棵 $\text{iTree}$, 然后计算最终落在每个树第⼏层. 然后我们可以得出在每棵树的⾼度平均值. 获得每个测试数据的平均深度后, 我们可以设置⼀个阈值, 其平均深度小于此阈值的即为异常.

2.5. Data Sampling

简单随机抽样: 从总体 $N$ 个单位中随机地抽取 $n$ 个单位作为样本, 使得每⼀个容量为样本都有相同的概率被抽中. 特点是: 每个样本单位被抽中的概率相等, 样本的每个单位完全独⽴, 彼此间⽆⼀定的关联性和排斥性.

分层抽样: 将抽样单位按某种特征或某种规则划分为不同的层, 然后从不同的层中独⽴、随机地抽取样本. 从而保证样本的结构与总体的结构⽐较相近, 从而提⾼估计的精度.

⽋采样和过采样: 在处理有监督的学习问题的时候, 我们经常会碰到不同分类的样本⽐例相差较⼤的问题, 这种问题会对我们构建模型造成很⼤的影响, 因此从数据⻆度出发, 我们可以利⽤⽋采样或过采样处理这种现象.

3. Data Transformation

3.1. Dimensionality Reduction

无量纲化: 归一化与标准化

归⼀化⼀般是指将数据的取值范围缩放到 $[0,1]$ 之间, 当然部分问题也可能会缩放到 $[-1,1]$ 之间. 针对⼀般的情况, 归⼀化的结果可以表⽰为:

$$x^{\prime}=\frac{x-x_{\min }}{x_{\max }-x_{\min }}\newline (x_{min}=\min_{x\in X} x\quad x_{max}=\max_{x\in X} x) $$

通过归⼀化, 我们可以消除不同量纲下的数据对最终结果的影响.

除了归一化之外, 我们还需要标准化. 标准化的⽬的是为了让数据的均值为 0, 标准差为 1, 标准化还称为 $\text{Z-score}$，标准化的结果可以表⽰为:

$$x^{\prime}=\frac{x-\bar{X}}{S} $$

通过标准化得到的新的数据均值为 0 和标准差为 1 的新特征, 这些新特征在后续处理中会有很多好处. 如：我们将标准差统⼀到 1，从信息论⻆度, ⽅差可以表⽰其中蕴含的信息量越大, 信息量越⼤对模型的影响就也⼤, 因此我们将其标准化到 1, 这样就消除了最开始不同变量具有不同的影响程度的差异. 除此之外, 去量纲化在利⽤梯度下降等⽅法求最优解的时候也具有重要的作⽤. 在利⽤梯度下降等⽅法求最优解的时候, 每次我们都会朝着梯度下降的最⼤⽅向迈出⼀步, 但当数据未经过去量纲化的原始数据时, 每次求解得到的梯度⽅向可能和真实的误差最小的⽅向差异较⼤, 这样就会可能导致收敛的速度 很慢甚⾄⽆法收敛. 而通过去量纲化后的数据, 其⽬标函数会变得更“圆”, 此时每⼀步梯度的⽅向和真实误差最小的⽅向的偏差就会⽐较小, 模型就可以很快收敛到误差最小的地⽅.

3.2. Binning

分箱是⼀种数据预处理技术, 用于减少次要观察误差的影响, 是⼀种将多个连续值分组为较少数量的“分箱”的⽅法. 分箱的⼀些优势如下:

  • 离散化后的特征对异常数据有更强的鲁棒性.
  • 逻辑回归属于⼴义线性模型, 表达能⼒受限, 单变量离散化为 $N$ 个后, 每个变量有单独的权重, 为模型引⼊了⾮线性, 提升模型表达能⼒, 加⼤拟合.
  • 离散化后可以进⾏特征交叉, 由 $M+N$ 个变量变为 $M\times N$ 个变量, 进⼀步引⼊⾮线性提升表达能⼒.
  • 可以将缺失作为独⽴的⼀类带⼊模型.
  • 将所有变量变换到相似的尺度上。

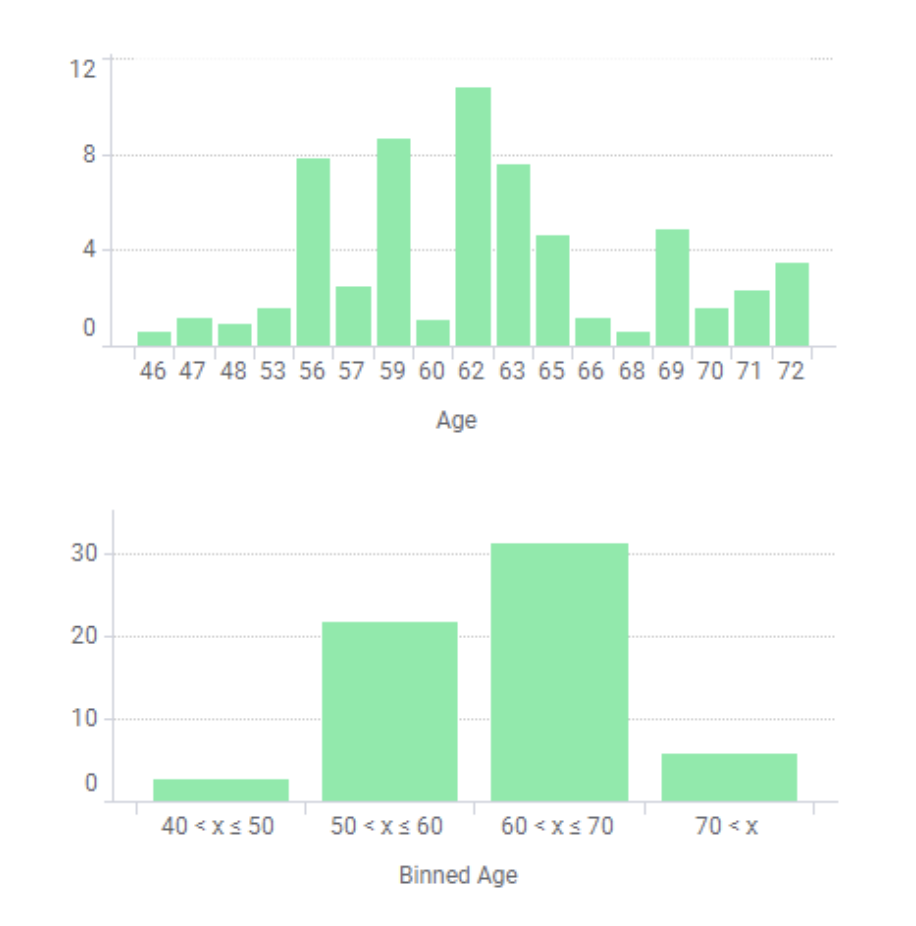
3.3. Data Encoding

分类标签编码与One-Hot编码, 比较trivial.

4. Extraction, Selection and Monitoring

4.1. Feature Extraction

⼈⼯特征提取: $\xcancel{\mathbf{SQL}\ \mathbf{SQL}\ \mathbf{SQL}}$

降维:

4.2. Feature Selection

特征选择本质上继承了奥卡姆剃⼑的思想, 从⼀组特征中选出⼀些最有效的特征, 使构造出来的模型更好.

  • 避免过度拟合, 改进预测性能
  • 使学习器运⾏更快, 效能更⾼
  • 剔除不相关的特征使模型更为简单，容易解释

过滤⽅法 (Filter Methods): 按照发散性或相关性对特征进⾏评分, 设定阈值或者待选择阈值的个数, 选择特征.

  • ⽅差选择法: 选择⽅差⼤的特征。
  • 相关关系 & $\chi^2$ 检验: 特征与⽬标值的相关关系.
  • 互信息法: ⼀个随机变量包含另⼀个随机变量的信息量.

封装⽅法 (Wrapper Methods): 是利⽤学习算法的性能来评价特征⼦集的优劣. 因此, 对于⼀个待评价的特征⼦集, Wrapper ⽅法需要训练⼀个分类器, 根据分类器的性能对该特征⼦集进⾏评价, 学习算法包括决策树、神经⽹络、 ⻉叶斯分类器、近邻法以及⽀持向量机等. Wrapper ⽅法缺点主要是特征通⽤性不强, 当改变学习算法时, 需要针对该 学习算法重新进⾏特征选择.

集成⽅法 (Embedded Methods): 在集成法特征选择中, 特征选择算法本⾝作为组成部分嵌⼊到学习算法⾥. 最典型的即决策树算法. 包括基于惩罚项的特征选择法和基于树模型的特征选择法.

4.3. Feature Monitoring

在数据分析和挖掘中, 特征占据着很重要的地位. 因此, 我们需要对重要的特征进⾏监控与有效性分析, 了解模型所⽤的特征是否存在问题, 当某个特别重要的特征出问题时, 需要做好备案, 防⽌灾难性结果.

  • 数据缺失
  • 数据异常
  • …

5. References

  1. Leo Van, Prompt Engineering, https://ds-python.leovan.tech/lecture/feature-engineering/ ↩︎

  2. Wikipedia, Feature engineering. https://en.wikipedia.org/wiki/Feature_engineering ↩︎

  3. Brownlee, Discover feature engineering, how to engineer features and how to get good at it. http://machinelearningmastery.com/discover-feature-engineering-how-to-engineer-features-and-how-to-get-good-at-it/ ↩︎

  4. T. Malisiewicz, What is feature engineering?. https://www.quora.com/What-is-feature-engineering ↩︎

  5. Rubin, Donald B. Inference and missing data. Biometrika 63.3 (1976): 581-592. ↩︎

  6. Allison, Paul D. Missing data. Vol. 136. Sage publications, 2001. ↩︎

  7. Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. Isolation forest. 2008 Eighth IEEE International Conference on Data Mining. IEEE, 2008. ↩︎

  8. Liu, Fei Tony, Kai Ming Ting, and Zhi-Hua Zhou. Isolation-based anomaly detection. ACM Transactions on Knowledge Discovery from Data (TKDD) 6.1 (2012): 1-39. ↩︎

  9. Leo Van, Maniford Learning, https://leovan.me/cn/2018/03/manifold-learning/ ↩︎