这份课件很烂
1. Origins
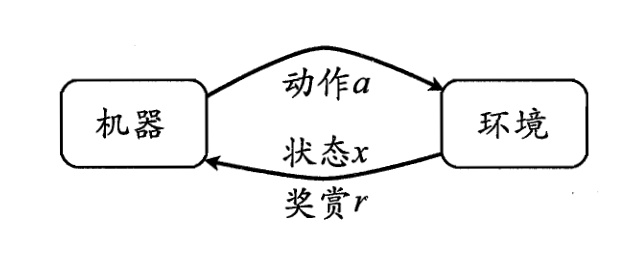
概念学习: 给定正例/反例,学习目标概念(如监督学习)
交互学习: 通过交互学习一个任务(如走出迷宫)
- 系统(或外部环境)存在若干个”状态”
- 学习算法/动作会影响”状态”的分布
- 潜在的 Exploration 和 Exploitation 折衷
2. MDP Model
Markov Decision Process (马尔可夫决策过程, MDP) 是一种离散时间随机控制过程.
Formally, MDP 由如下的几个部分构成:
- $S$-set of states, 状态集合
- $A$-set of actions, 动作集合
- 目标: 最大化期望奖赏(单状态下)
- $\delta$-transition probability, 状态转移概率
- $R$–immediate reward function, 即时奖赏函数
值得注意的是, 这里的奖赏函数是需要仔细设计的. 有很多值得考虑的问题:
- 轨迹中早期的奖赏和晚期的奖赏相比, 谁更重要?
- 系统是持续的, 还是有终止状态的?
通常返回函数是即时奖赏值的线性组合
$\textbf{Finite Horizon}$: $\displaystyle \text{return}=\sum_{i=1}^H R(s_i,a_i)$
$\textbf{Infinite Horizon}$
- 有折扣: $\displaystyle \text{return}=\sum_{i=0}^{\infty} \gamma^i R(s_i,a_i)$
- 无折扣: $\displaystyle \text{return}=\lim_{n\to +\infty}\frac 1 n\sum_{i=0}^{n-1} R(s_i,a_i)$
3. DP
$\textbf{Optimal Control}$: 寻找一个最优策略$π^*$ (从任一状态出发, 其返回值都为最大)
3.1. value Functions
$V_π(s)$: 从 $s$ 状态出发, 采用 $π$ 策略, 所获得的期望返回值
$Q_π(s,a)$: 从 $s$ 状态出发, 采用 $a$ 动作, 继而采用 $π$ 策略, 所获得的期望返回值
最优值函数 $V^*(s)$ and $Q^*(s,a)$: 采用最优策略 $π^*$ 所获得的期望
返回值定理: 策略 $π$ 为最优策略当且仅当, 在每一个状态$s$
$$\begin{align}
V^*(s) = \max_{\pi}V_π (s) \\
V_π(s) = \max_aQ_π(s,a)
\end {align}
$$
4. Reinforcement Learning
4.1. Concepts
监督学习: (正/反例)在样本上的分布是确定的
强化学习: (状态/奖赏)的分布是策略依赖的 (policy dependent), 策略上小的变化都会导致返回值的巨大改变
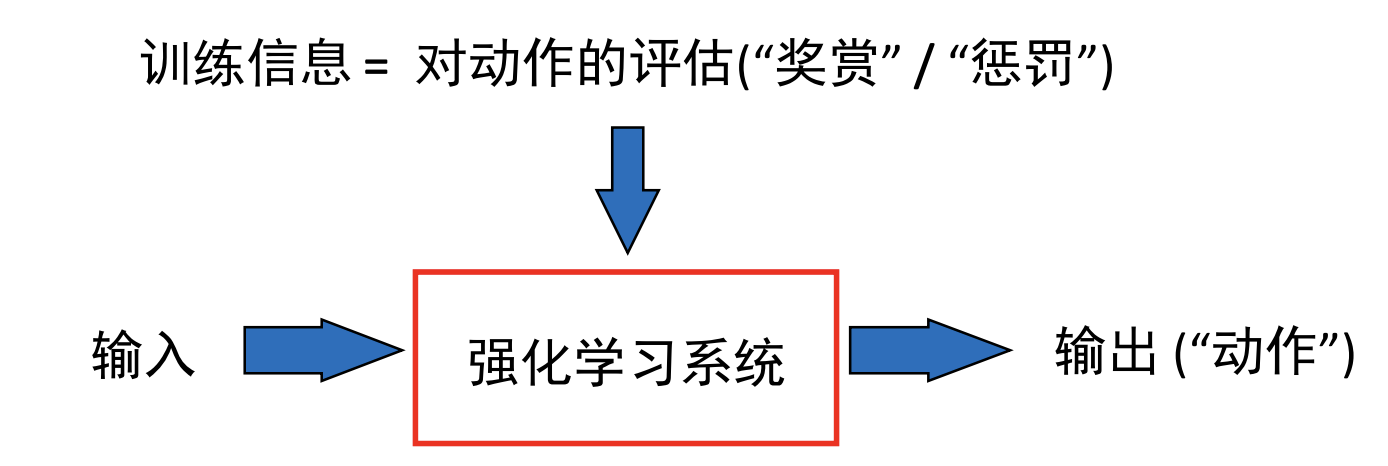
强化学习要素
- 策略: 选择动作的(确定/不确定)规则
- 奖赏/返回: 学习系统试图最大化的函数
- 值函数: 评估策略好坏的函数
- 模型: 环境(问题)演变遵循的法则
4.2. Monte Carlo Method
关于 $\text{Monte Carlo}$ 方法可以查看我的这篇数学建模笔记
- MC策略迭代: 使用MC方法对策略进行评估, 计算值函数
- MC策略修正: 根据值函数(或者状态-动作对值函数), 采用贪心策略进行策略修正
$$V(s_t)\leftarrow V(s_t) + α[R - V(s_t)]
$$
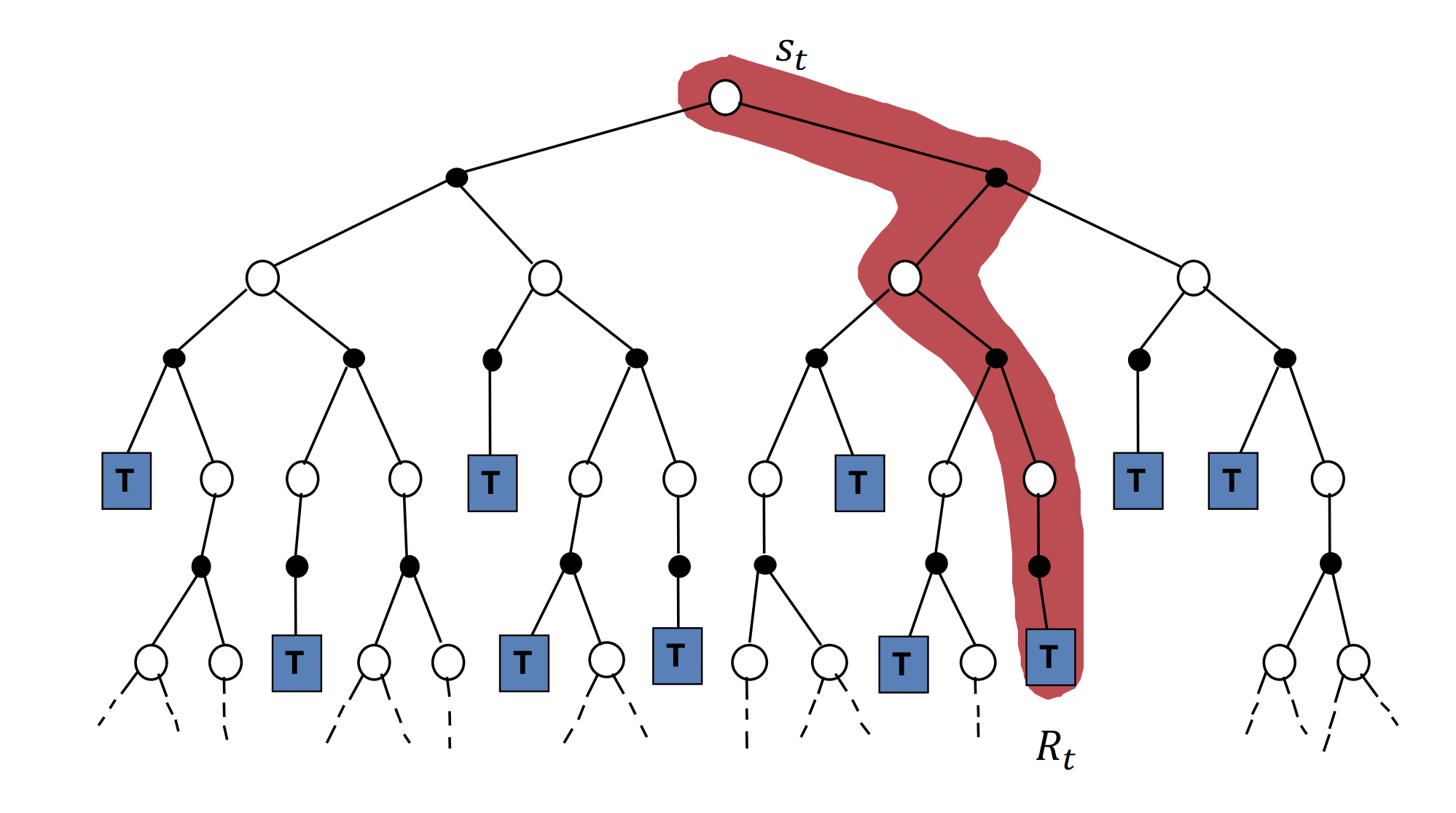
cont.