Database Indexing

CS › DBMS

1. B+ Tree Indexing

Clustered Index vs. Non-clustered Index

  • Clustered Index (聚集索引): The leaf nodes of the index contain the actual data rows of the table. The index is built on the same key as the table, and the data rows are stored in order of the index key.
  • Non-clustered Index (非聚集索引): The leaf nodes of the index do not contain the actual data rows of the table. Instead, they contain pointers to the data rows.

不同的数据库系统对聚集索引的支持和默认行为各不相同:

  • Microsoft SQL Server: 在SQL Server中, 当你为表定义一个主键时, 默认会为该主键创建一个聚集索引, 除非你显式指定不这么做. 如果不定义聚集索引, SQL Server允许表以堆的形式存储 (即没有排序的数据结构.
  • MySQL: 在MySQL中, InnoDB存储引擎默认使用聚集索引来存储表数据. 每个InnoDB表都有一个聚集索引, 如果定义了主键, 聚集索引就是主键. 如果没有显式定义主键, MySQL会选择一个唯一索引作为聚集索引；如果没有唯一索引, InnoDB会自动生成一个隐藏的行ID作为聚集索引.
  • Oracle: Oracle数据库不自动创建聚集索引. 相反, Oracle使用一个名为“索引组织表”的特殊表类型来实现类似聚集索引的行为. 在索引组织表中, 表数据是根据主键索引顺序存储的.
  • PostgreSQL: 默认情况下, PostgreSQL不使用聚集索引, 而是使用一种称为“堆”的结构来存储表中的数据. 不过, 你可以使用CLUSTER命令按某个索引的顺序重新组织表中的数据, 这与聚集索引有类似的效果, 但这种物理排序不是自动维护的.

2. Hash-based Indexing

Hash-based indexing is useful for equality selections, but not for range searches. B+ trees are more versatile.

由于 Hash Indexing 不能支持区间查询, 所以它不是绝大部分数据库的默认索引类型. 但是绝大部分数据库都支持 Hash Indexing, 用于支持等值查询.

2.1. Static Hashing

Static hashing is like what we have learnt in a normal data structrue course. It is a fixed-size hash table that maps keys to buckets.

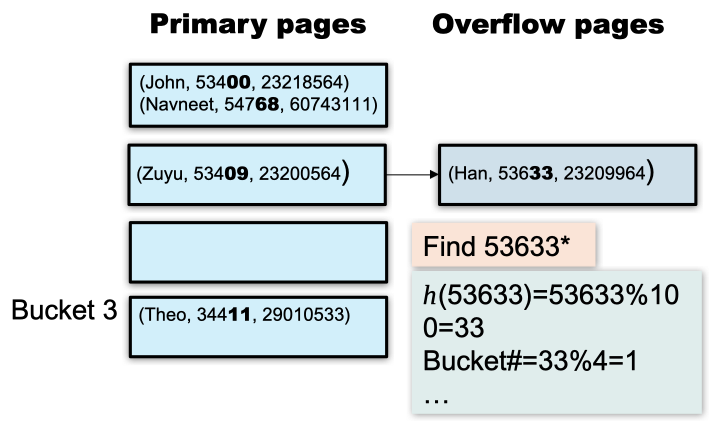
However static hashing is not so efficient when it comes to the context of database, since number of buckets in the index is fixed:

  • If the database grows, the number of buckets will be too small, and long overflow chains can degrade performance
  • If the database shrinks, space is wasted
  • Reorganizing the index is expensive and can block query execution

So we need a more dynamic hashing scheme.

2.2. Dynamic Hashing

AKA. Extendible Hashing

Dynamic hashing allows the hash function to be modified dynamically

3. Sorting

Why does DBMS need sorting?

  • Sorting is used for searching/retrieving data easier
  • Users usually want the returned results sorted
  • Sorting used in Joins (future topics)
  • Sorting is first step in bulk-loading a B+ tree
  • Sorting useful for eliminating duplicates

Why don’t these sorting algorithms work well in DBMS?

  • Quicksort
  • Mergesort
  • Heapsort
  • Selection sort
  • Insertion sort
  • Bubble sort

Because they are not designed for external sorting, which means they are not designed to handle data that is too large to fit in memory at once.

  • Internal Sorting (data is in memory at all time while the sorting is in progress)
    Heapsort, Quicksort
  • External Sorting (data is stored on disk and only small chunks are loaded inside the memory)
    2-way merge sort, Multiway Mergesort
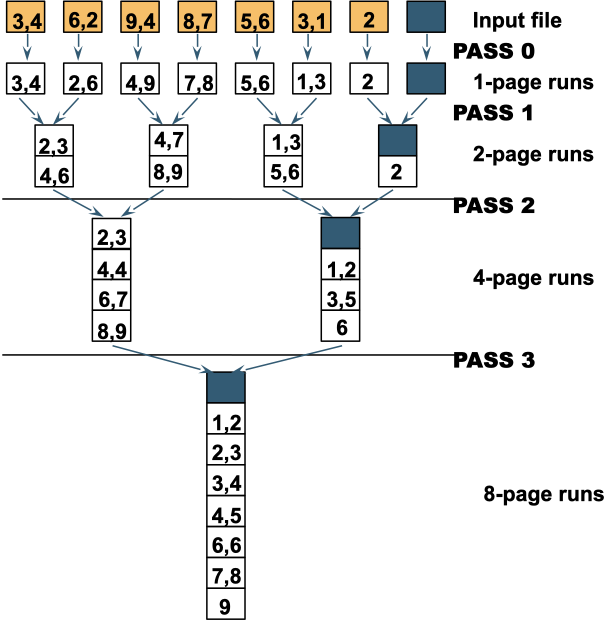
merge sort

Suppose there are $N$ pages in the file, and $B$ ways to merge.

  • The number of passes required to sort the file is $\lceil\log_{B-1} \rceil N$
  • The number of I/Os required to sort the file is $2N \lceil \log_{B-1} N\rceil$

4. Join Algorithms

Various algorithms for joining two relations:

  • Nested Loop Join
  • Block Nested Loop Join
  • Index Nested Loop Join
  • Block Index Nested Loop Join
  • Sort-merge Join
  • Hash Join

We consider such an example of two relations R and S:

R = Reserve

  • Each tuple is 40 bytes long.
  • 100 tuples per page.
  • 1000 pages. ~100,000 tuples.

S = Sailor

  • Each tuple is 50 bytes long.
  • 80 tuples per page.
  • 500 pages. ~40,000 tuples.

4.1. Simple Nested Loop Join

1
2
3
4
for tuple r in R:
    for tuple s in S:
      if r.x == s.x:
        result.add(r, s)

In this case there would be around T(R) * T(S) = 100,000 * 40,000 = 4,000,000,000 I/Os.

Assuming that each I/O takes 10ms -> this will take about 11,111 hours.

4.2. Block Nested Loop Join

1
2
3
4
5
for block in R:
    build a hash table on R-block 
    for S page:
      for each matching tuple r in R-block, s in S-page:
        result.add(r, s)
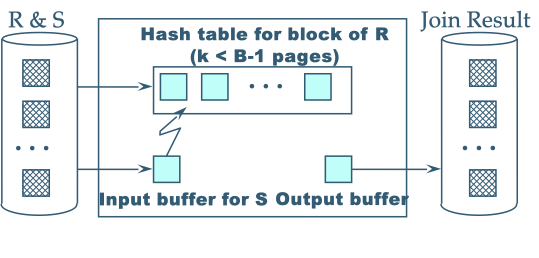
nested loop join

Assuming that each I/O takes 10ms -> this will take about 1 minute.

4.3. Index Nested Loop Join

Given the index of R on attribute x (which is the common attribute with S), we can use the index to retrieve the corresponding tuple in R for each tuple in S.

1
2
3
4
for s in S:
  retrieve corresponding r with r.x = s.x from given index
  if r is not null:
    result.add(r, s)

4.4. Block Index Nested Loop Join

Improve performance using available buffer pages

1
2
3
4
5
6
for each block of B-2 pages of R:
  Sort the tuples in the current block (in memory)
  for each tuple t_R in the current sorted block:
    Probe the index on S to find any tuples matching t_R 
      if found:
        concat them and output

4.5. Sort-Merge Join

Assuming x is the primary key of R and S.

1
2
3
4
5
6
7
8
9
10
11
Sort R and S on join column using external sorting. 
  Merge R and S on join column
  output result tuples. 
while R is not finished and S is not finished:  
  # Scanning:
  Advance scan of R until current R-tuple >=current S tuple, 
  Advance scan of S until current S-tuple>=current R tuple; 
  Do this until current R tuple = current S tuple. 
  # Matching: 
  Match all R tuples and S tuples with same value
  output <r, s> for all pairs of such tuples.

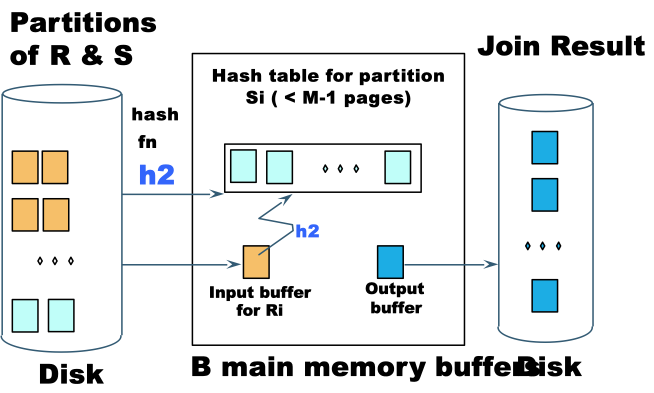
4.6. Hash Join

1
2
3
4
5
build index of R on attribute X
for s in S:
  r = use index of R to find (s.x)
  if r is not null:
    result.add(r, s)

Suppose the table is too big to fit in memory, we can use Partitioned Hash Join

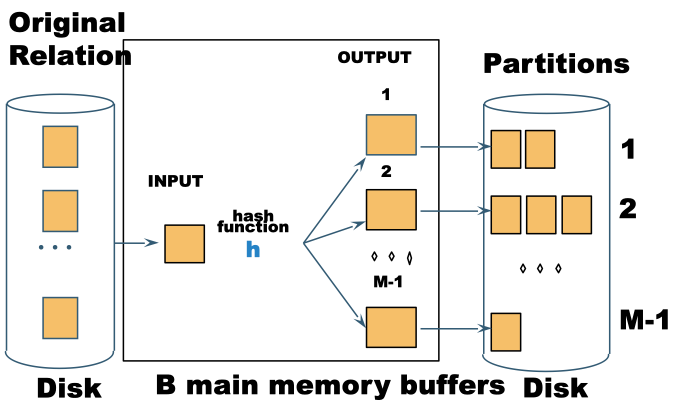
hash join
  1. Hash S into $M-1$ buckets, and send all buckets to disk.
  2. Hash R into $M-1$ buckets with the same hash function and send all buckets to disk
  3. Join every pair of buckets
hash join