Correlation Coefficient

$$\huge\textbf{Correlation Coefficient} $$

1. Intro

统计学上, 我们用相关系数来衡量两个变量之间的相关性的大小. 根据数据满足的不同条件, 我们选取不同的相关系数. 在这里我们主要研究 $\text{Pearson}$ 相关系数和 $\text{Spearman}$ 等级相关系数.

关于 $\text{Pearson}$ 相关系数最基本的介绍, 可以查看我的这篇数据科学笔记. 在统计学中, 要特别注意是样本的统计量还是总体的统计量.

2. $\text{Pearson}$ Correlation Coefficient

2.1. Definitions

统计学的一个最基本的问题是, 计算抽取的样本的统计量来估计总体的统计量. 例如使用样本均值, 样本标准差来估计总体的均值 (平均水平) 和总体的标准差 (偏离程度).

如果说有总体 $X:\left\{X_{1}, X_{2}, \cdots, X_{n}\right\}, Y:\left\{Y_{1}, Y_{2}, \cdots, Y_{n}\right\}$, 那么总体协方差为:

$$\operatorname{Cov}(X, Y)=\frac{\displaystyle\sum_{i=1}^{n}\left(X_{i}-E(X)\right)\left(Y_{i}-E(Y)\right)}{n} $$

直观理解协方差: 如果 $X$, $Y$ 变化方向相同, 即当 $X$ 大于 (小于) 其均值时, $Y$ 也大于 (小于) 其均值, 在这两种情况下, 乘积为正. 如果 $X$, $Y$ 的变化方向一直保持相同, 则协方差为正; 同理, 如果 $X$, $Y$ 变化方向一直相反, 则协方差为负; 如果 $X$, $Y$ 变化方向之间相互无规律, 即分子中有的项为正, 有的项为负, 那么累加后正负抵消.

注意: 协方差的大小和两个变量的量纲有关, 因此不适合做比较.

为了找到一个适合进行比较的统计量, 我们可以考虑使用总体 $\text{Pearson}$ 系数:

$$\rho_{XY}:=\frac{\operatorname{Cov}(X,Y)}{\sigma_X\sigma_Y}\\ $$

相对应的, 如果说有样本 $X:\left\{X_{1}, X_{2}, \cdots, X_{n}\right\}, Y:\left\{Y_{1}, Y_{2}, \cdots, Y_{n}\right\}$, 那么样本协方差为:

$$\operatorname{Cov}(X, Y)=\frac{\displaystyle\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)\left(Y_{i}-\bar{Y}\right)}{n-1} $$

对应的样本 $\text{Pearson}$ 相关系数为:

$$r_{X Y}=\frac{\operatorname{Cov}(X, Y)}{S_{X} S_{Y}} $$

值得注意的是, Pearson相关系数只能衡量两个线性相关变量之间的相关程度.

“In statistics, the Pearson product‐moment correlation coefficient is a measure of the linear correlation (dependence) between two variables $X$ and $Y$, giving a value between +1 and −1 inclusive, where 1 is total positive correlation, 0 is no correlation, and −1 is total negative correlation. It is widely used in the sciences as a measure of the degree of linear dependence between two variables.”

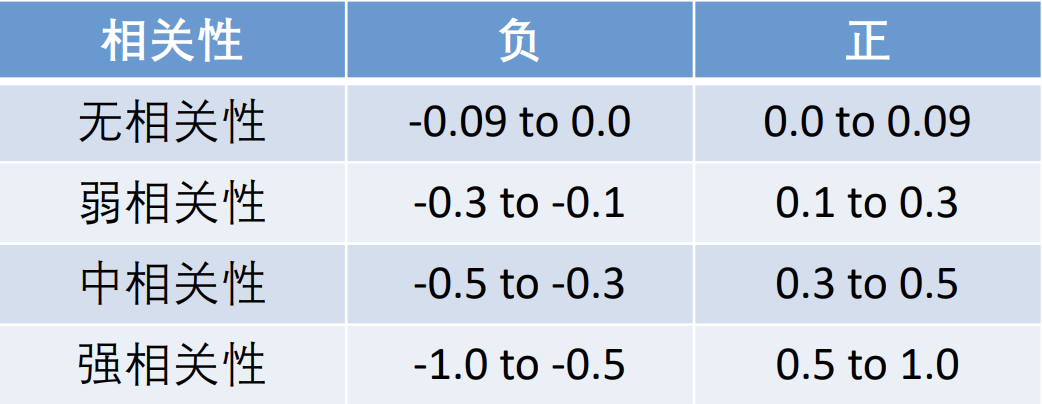
• 如果两个变量本身就是线性的关系, 那么皮尔逊相关系数绝对值大的就是相关性强, 小的就是相关性弱;
• 在不确定两个变量是什么关系的情况下, 即使算出皮尔逊相关系数很大, 也不能说明那两个变量线性相关, 甚至不能说他们相关, 我们一定要画出散点图来看才行.

2.2. Hypothesis Test

关于假设检验的部分, 可以查看我的这篇数据科学笔记

第一步：提出原假设 $H_0$ 和备择假设 $H_1$
假设我们计算出了一个皮尔逊相关系数 $r$, 我们想检验它是否显著的异于 $0$. 那么我们可以这样设定原假设和备择假设:

$$\begin{align} H_0:r=0\\ H_1:r\not=0 \end{align} $$

第二步：在原假设成立的条件下，利用我们要检验的量构造出一个符合某一分布的统计量

统计量相当于我们要检验的量的一个两数，里面不能有其他的随机变量

这里的分布一般有四种: 标准正态分布, $t$ 分布, $\chi^2$分布和 $F$ 分布. 对于 $\text{Pearson}$ 相关系数 $r$ 而言, 在满足一定条件下, 我们可以构造统计量:

$$t=r \sqrt{\frac{n-2}{1-r^{2}}} $$

可以证明 $t$ 是服从自由度为 $n-2$ 的 $t$ 分布.

第三步: 将我们了要检验的这 个值带入这个统计量中, 可以得到一个特定的值 (检验值)

第四步: 由于我们知道统计量的分布情况, 因此我们可以画出该分布的概率密度两数 $pdf$, 并给定一个置信水平, 根据这个置信水平查表找到临界值, 并画出检验统计量的接受域和拒绝域.

第五步: 看我们计算出来的检验值是落在了拍绝域还是按受域, 并下结论.

2.3. Conditions

$\text{Pearson}$ 相关系数假设检验需要满足一定的条件

• 实验数据通常假设是成对的来自于正态分布的总体. 因为我们在求 $\text{Pearson}$ 相关性系数以后, 通常还会用 $t$ 检验之类的方法来进行皮尔逊相关性系数检验, 而 $t$ 检验是基于数据呈正态分布的假设的.
• 实验数据之间的差距不能太大. $\text{Pearson}$ 相关性系数受异常值的影响比较大
• 每组样本之间是独立抽样的. 构造 $t$ 统计量时需要用到

这里引入两种方法, 来判断数据是否很大程度上可能符合正态分布.

1. $\text{Jarque‐Bera}$ Test

雅克‐贝拉检验常用于大样本 ($n>30$)

对于一个随机变量 $\{X_i\}$, 假设其偏度为 $S$, 峰度为 $K$, 那么我们可以构造 $JB$ 统计量:

$$J B=\frac{n}{6}\left[S^{2}+\frac{(K-3)^{2}}{4}\right] $$

可以证明, 如果 $\{X_i\}$ 是正态分布, 那么在大样本情况下 $JB\sim\chi^2(2)$.

注: 正态分布的偏度为 $0$, 峰度为 $3$

2. $\text{Shapiro‐wilk}$ Test

Shapiro-wilk检验常用与小样本: $3≤n≤50$

这个我只会调包

3. $\text{Q-Q}$ graph

$\text{Q‐Q}$ 图 (Q代表分位数Quantile) 是一种通过比较两个概率分布的分位数对这两个概率分布进行比较的概率图方法. 首先选定分位数的对应概率区间集合, 在此概率区间上, 点 $(x,y)$ 对应 于第一个分布的一个分位数 $x$ 和第二个分布在和 $x$ 相同概率区间上相同的分位数. 这里, 我们选择正态分布和要检验的随机变量, 并对其做出 $\text{Q-Q}$图, 可想而知, 如果要检验的随机变量是正态分布, 那么 $\text{Q-Q}$ 图就是一条直线. 要利用 $\text{Q‐Q}$ 图鉴别样本数据是否近似于正态分布, 只需看图上的点是否近似地在一条直线附近. (要求数据量非常大)

3. $\text{Spearman}$ 相关系数

3.1. Definitions

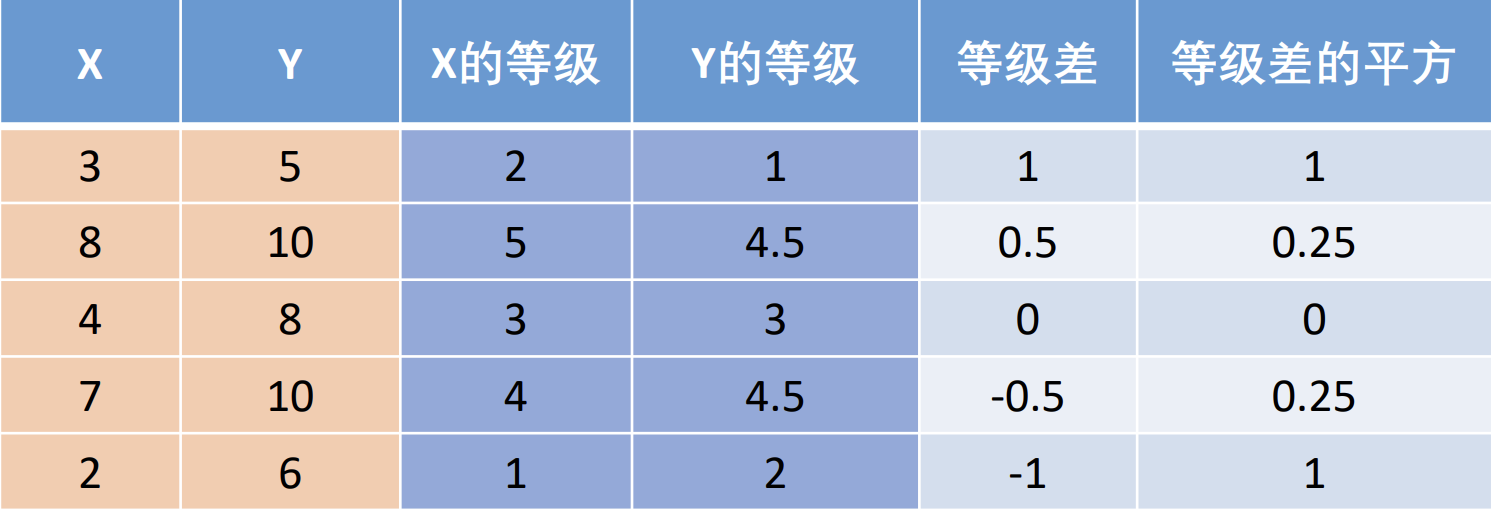
如果 $X,Y$ 为两组数据, 那么其 $\text{Spearman}$ (等级) 相关系数定义为:

$$r_{s}=1-\frac{6 \displaystyle\sum_{i=1}^{n} d_{i}^{2}}{n\left(n^{2}-1\right)} $$

其中, $d_i$ 为 $X_i$ 和 $Y_i$ 之间的等级差. 通过一些初等代数的变形可以证明 $-1\le r_s\le 1$.

一个数的等级, 就是将它所在的一列数按照从小到大排序后, 这个数所在的位置. 如果有的数值相同, 则将它们所在的位置取算术平均.

如果样本数目不太大 ($n\le30$), 直接查临界值表即可. 如果样本数目比较大, 由于在大样本情况下有:

$$\begin{align} r_s\sqrt{n-1}\sim\mathbb N(0,1)\\ H_0:r_s=0\quad H_1:r_s\not =0 \end{align} $$

我们计算 $r_s\sqrt{n-1}$, 并求出对应的 $p$ 值与 $0.05$ 比较即可.

3.2. Differentiations

$\text{Spearman}$ 相关系数和 $\text{Pearson}$ 相关系数选择

• 连续数据, 正态分布, 线性关系, 用 $\text{Pearson}$ 相关系数是最恰当, 当然用$\text{Spearman}$ 相关系数也可以, 就是效率没有 $\text{Pearson}$ 相关系数高.
• 上述任一条件不满足, 就用$\text{Spearman}$ 相关系数, 不能用 $\text{Pearson}$ 相关系数.
• 两个定序数据之间也用$\text{Spearman}$ 相关系数, 不能用$\text{Pearson}$ 相关系数.