Congruence Problems

Chentian Wu

2024-11-19

\renewcommand{\N}{\mathbb N} \renewcommand{\Z}{\mathbb Z} \renewcommand{\C}{\mathbb C} \renewcommand{\Q}{\mathbb Q} \renewcommand{\R}{\mathbb R} \renewcommand{\1}{\textbf{1}} \renewcommand{\argmin}{\text{argmin}}

1. Euclidean Domains

Definition. Euclidean (integral) domain
An integral domain $$D$$ is called Euclidean, if there is a map $$v$$ called the Euclidean function

v : D\setminus\{0\}\to \N

such that

\forall a, b\in D,b \neq 0\quad \exists q, r\in D, a = qb+r

such that either $$r = 0$$ or $$v(r) < v(b)$$ . The process of finding such $$q$$ and $$r$$ is called division with remainder and $$v$$ is called the Euclidean function.

Example.

$\Z$ is an Euclidean domain with $v:n\mapsto |n|$
The Gaussian integer ring $\Z[i] = \{a + bi \mid a, b ∈ \Z\} \subset \C$ is an Euclidean domain with Euclidean function $z\mapsto \|z\|^2$
(long division) The polynomial ring $R=\R[x]$ is an Euclidean domain with Euclidean function defined as $f\mapsto \deg(f)$

Theorem. Let $$D$$ be an Euclidean domain, then any ideal $$I$$ of $$D$$ can be written as

I = \{ra \mid r \in D\}

for some $a\in I$ .
Pf. Suppose $$v$$ is the Euclidean function of $$D$$ .

If $I=\{0\}$ , then $I=\{r0\mid r\in R\}$
Otherwise let $a=\argmin_{r\in R}v(r)$ . Since $$D$$ is an Euclidean domain, $\forall b\in I. b=ca+r$ and $r\in R$ , this indicates

Definition. Principal ideal (主理想)
An ideal generated by a single element $a\in R$ is called a principal ideal. Denoted by $$(a)$$ . Here $$a$$
is called the generator of this ideal.

If the generator exists, it’s unique up to a unit factor ( $$2$$ and $$-2$$ are both generate $\Z$ )

Note. Given a ring $$R$$ ,

If $$I$$ is a principal ideal of $$R$$ , then $$I$$ is of the form $\{ra\mid r\in R\}$ . This is because $$I$$ is a ideal and $$I$$ is a principal ideal. So every principal ideal has a generator.
Given any arbitrary $a\in R$ , $\{ra\mid r\in R\}$ is not necessarily a ideal. But as long as it’s an ideal, it’s then a principal ideal.
If $$R$$ is a commutative ring, given any $a\in R$ , we have $Ra:=\{ra\mid r\in R\}$ is a principal ideal.

Definition. Principal ideal domain (PID)
An integral domain whose every ideal is principal is called a principal ideal domain (PID).

Definition. Greatest common divisor
Let $$D$$ be an PID. Given $a, b\in D$ , the generator of $(a,b)=\{ra+sb\mid r,s\in D\}$ is called the greatest common divisor of $$a$$ and $$b$$ , denoted by $\gcd(a,b)$ .
Why is gcd well defined? we know $$(a)$$ and $$(b)$$ are of the form

\begin{aligned} (a)&=\{ra\mid r\in D\}\\ (b)&=\{sb\mid s\in D\} \end{aligned}

Consider $(a, b)=\{ra+sb\mid r,s\in D\}$ . Since $$(a, b)$$ is the sum of two ideals, we know its then a new ideal. Since $$D$$ is a PID, so $$(a,b)$$ is principal, so it should have a generator $$c$$ such that

$$(c)=(a,b) $$

Note. (Foote, Dummit, P274 Definition) another definition of $\gcd$ .
We should know that the concept of $\gcd$ is not limited to PID. If $$R$$ is a commutative ring with identity, $a, b\in R$ , $b\neq 0$ , then

$$a$$ is said to be a multiple of $$b$$ if there exists an element $x\in R$ such that $$a=bx$$ . In this case we say $$b$$ is a divisor of $$a$$ or $$b$$ divides $$a$$ , denoted by $b\mid a$ .
The greatest common divisor of $a$ and $b$, denoted by $\gcd(a,b)$, is a nonzero element $d$ such that
1. $d\mid a$ and $d\ mid b$
2. If $d'\mid a$ and $d'\mid b$ then $d'\mid d$

Note. Any Euclidean domain is a PID.

Example. There are some integral domains that are not PIDs. Consider $R=\Z[x]$ as the polynomial ring with integral coefficients, it could then be proved that

(x,2):=\{xf+2g\mid f,g\in R\}

is not a PID. (prove by contradiction, discuss $\deg h$ for $h\in (x,2)$ )

Theorem. Bezout’s theorem.
Let $$D$$ be a PID. $c=\gcd(a,b)$ iff there exists $t,s,m,n\in D$ such that $$c=ta+sb$$ , $$a=mc$$ and $$b=nc$$ .

The question of finding such $$t,s,m,n$$ is called Bezout’s problem.

Algorithm. Euclidean’s algorithm

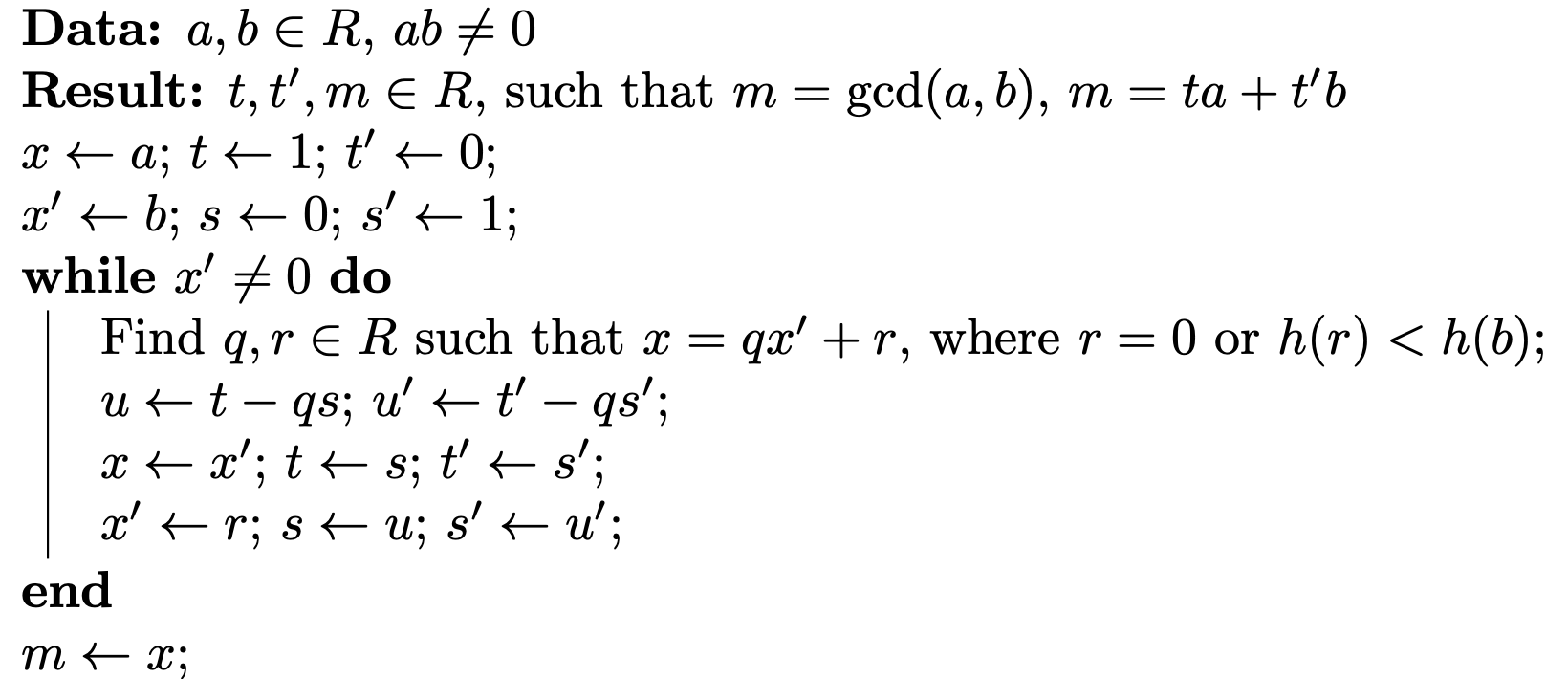
An example of this algorithm on $\Z$ implemented using Python is as follows

import sys 
a=int(sys.argv[1]) 
b=int(sys.argv[2])
if a * b == 0: 
	 exit() 
def euclid(a, b): 
	x = [a, b] 
	t = [1, 0] 
	s = [0, 1] 
	while x[1] != 0: 
		r = x[0] % x[1] 
		q = (x[0] − r ) // x[1] 
		u=[u − q * v for u, v in zip(t, s)] 
		x[0]= x[1]; t = s
		x[1]= r; s = u 
	return t[0], t[1], x[0] 
print(euclid(a, b))

Definition. Coprime of two ideals
Let $$R$$ be a commutative ring with identity $\1$ . We say two ideals $$I$$ and $$J$$ are coprime, if

I+J=\{a+b\mid a\in I,b\in J\}=(\1)=R

We say two elements $a,b\in R$ are coprime if the ideals $$(a)$$ and $$(b)$$ are coprime.

2. Unique Factorization

Definition. Prime
An element $p\in R$ where $$R$$ is a ring is called a prime if $$(p)$$ is a prime ideal

Another classical definition of prime (shown in hw) is that
In a commutative ring $$R$$ with identity, an element $$p$$ is said to be a prime if $p\mid ab\implies p\mid a$ or $p\mid b$ . Here, the “ $\mid$ ” notation means: $a\mid b$ iff there exists $r\in R$ s.t. $$b=ra$$ .

Definition. Several definitions regarding primes
Let $$R$$ be an integral domain,

If $r\in R$ is nonzero and not a unit. If $$r=ab$$ for some $a, b\in R$ , at least one of $$a$$ and $$b$$ must be a unit in $$R$$ , $$r$$ is said to be irreducible. Otherwise $$r$$ is said to be reducible.
Two elements $a,b\in R$ differing by a unit are said to be associate in $$R$$ (i.e. $$a=ub$$ for some unit $u\in R$ ).

Theorem. (Dummit Prop 8.3.10) In an integral domain, any prime is irreducible.

Definition. Unique factorization domain
An integral domain $$D$$ is said to have a unique factorization (UFD) if for any non-zero element $x\in D$ , either $$x$$ is a unit or there are primes $p_1, p_2,\ldots,p_r$ such that

x=\prod_{i=1}^r p_i

This is called a prime factorization. Moreover, if another prime factorization exists, say

x=\prod_{i=1}^sq_i

then

$$r=s$$ , and
after relabeling, there are units $$u_i$$ such that $$p_i=u_iq_i$$ ( $$p_i$$ and $$q_i$$ are associate for each $$i$$ )

Example.

$\Z$ is a UFD ( $6=2\times 3=(-2)\times (-3)$ )
Gaussian integer ring $\Z[i]$ is a UFD
$\Q[x]$ , the set of all polynomials with rational coefficients, is a UFD

Theorem. Any Euclidean domain is UFD
In particular, Euclidean domain $\subset$ PID $\subset$ UFD

Theorem. (Dummit Prop 8.3.12) In an UFD, a nonzero element is a prime iff it’s irreducible.

This theorem is so good that we can use the fact that a prime is irreducible in UFD.

3. Chinese Remainder Theorem

Theorem. Chinese Remainder Theorem
Let $$R$$ be a commutative ring with identities, $I_1, I_2,\ldots, I_n$ are ideals of $$R$$ that are pairwise coprime. Then the map

\begin{aligned} Q:R&\to(R/I_1)\times(R/I_2)\ldots\times (R/I_n)\\ r&\mapsto (r+I_1, r+I_2,\ldots, r+I_n) \end{aligned}

is surjective.