MATH►Mathematical Logic

1. Sentential Logic

$$\newcommand{\vD}{\vDash} \newcommand{\mS}{\mathcal S} \newcommand{\mE}{\mathcal E} \newcommand{\te}{\models=\!\mid} \huge\textbf{Sentential Logic} $$

这份笔记是用来记录数理逻辑的诸多定义和定理的, 以加强记忆. 所有的笔记都基于 A Mathematical Introduction to Logic

1. The Language of Sentential Logic

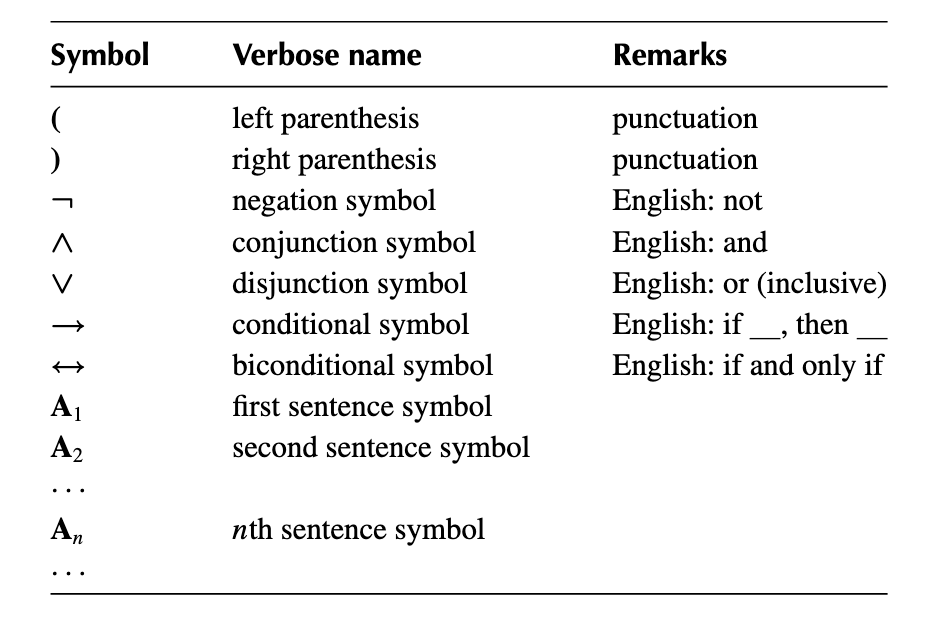
All Possible Symbols

$def: \textbf{sentential connective symbols}$ (命题连接符)

$$¬, ∧, ∨, →, ↔ $$

The 5 symbols above are called sentential connective symbols.

$def:\textbf{logical symbols}$

logic symbols are sentential connective symbols and parentheses

$def: \textbf{Sentence Symbol}$

The sentence symbols which are often denoted as $\mathbf{A_n}$ are the parameters (or nonlogical symbols).

$def: \textbf{Proposition Symbol}$

Proposition (命题) is what a sentence asserts.

命题就是肯定语句, 命题逻辑就是语句逻辑

We have assumed that no symbol is a finite sequence of other symbols. The purpose of this assumption is to assure that finite sequences of symbols are uniquely decomposable.

$def: \textbf{Expression}$

An expression is a finite sequence of symbols.

$def: \textbf{Well-formed Formulas}$
We want to define the well-formed formulas (wffs) to be the “grammatically correct” expressions; the nonsensical expressions must be excluded. The definition will have the following consequences:

  • Every sentence symbol is a wff.
  • If $α$ and $β$ are wffs, then so are $(¬ α)$, $(α ∧ β)$, $(α ∨ β)$, $(α → β)$, and $(α ↔ β)$.
  • No expression is a wff unless it is compelled to be one by (a) and (b).

More precisely, A well-formed formula (or simply formula or wff ) is an expression that can be built up from the sentence symbols by applying some finite number of times the formula-building operations (on expressions) defined by the equations:

$$\begin{aligned} \mathcal{E}_{\neg}(\alpha) & =(\neg \alpha) \\ \mathcal{E}_{\wedge}(\alpha, \beta) & =(\alpha \wedge \beta), \\ \mathcal{E}_{\vee}(\alpha, \beta) & =(\alpha \vee \beta), \\ \mathcal{E}_{\rightarrow}(\alpha, \beta) & =(\alpha \rightarrow \beta), \\ \mathcal{E}_{\leftrightarrow}(\alpha, \beta) & =(\alpha \leftrightarrow \beta) .\end{aligned} $$

$\textbf{INDUCTION PRINCIPLE}$

If $S$ is a set of wffs containing all the sentence symbols and closed under all five formula-building operations, then $S$ is the set of all wffs.

2. Truth Assignments

$def: \textbf{Truth Values}$

A truth values set is $\{T, F\}$, where

$$\begin{aligned} & F: \text{called \textit{falsity}}\\ & T: \text{called \textit{truth}} \end{aligned} $$

$def: \textbf{Truth Assignment}$

A truth assignment $v$ for a set $\mathcal S$ of sentence symbols is a function

$$v :\mathcal S \to \{F, T\} $$

assigning either $T$ or $F$ to each symbol in $\mathcal S$.

$def: \textbf{Extension Set \& Extension Assignment}$

Let $\mathcal {\bar S}$ be the set of wffs that can be built up from $\mathcal S$ by the five formula-building operations. ($\mathcal {\bar S}$ can also be characterized as the set of wffs whose sentence symbols are all in $\mathcal S$; see the remarks at the end of the preceding section.) We want an extension $\bar v$ of $v$,

$$\bar v : \bar S → \{F, T\}, $$

that assigns the correct truth value to each wff in $\mathcal {\bar S}$. It should meet the following conditions:

  1. $\forall A ∈ \mathcal S: \bar v(A) = v(A)$. (这也是为什么叫扩展 [extension])

$\forall \alpha,\beta \in \bar \mS$:

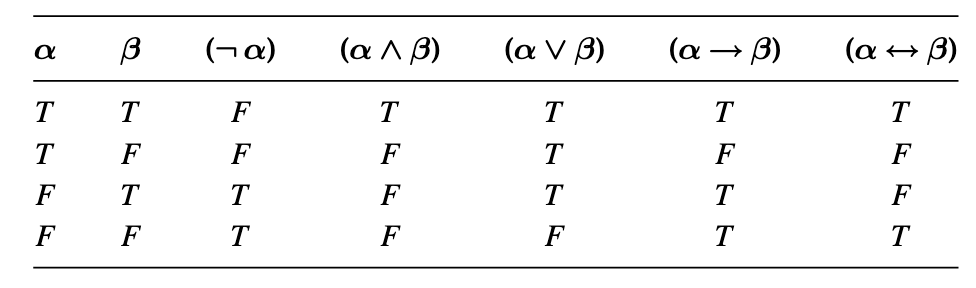
  1. $$\bar{v}((\neg \alpha))=\left\{\begin{array}{ll}T & \text { if } \bar{v}(\alpha)=F \\ F & \text { otherwise }\end{array}\right.$$
  2. $$\bar{v}((\alpha \wedge \beta))=\left\{\begin{array}{ll}T & \text { if } \quad \bar{v}(\alpha)=T \quad \text { and } \quad \bar{v}(\beta)=T \\ F & \text { otherwise. }\end{array}\right.$$
  3. $$\bar{v}((\alpha \vee \beta))=\left\{\begin{array}{ll}T & \text { if } \quad \bar{v}(\alpha)=T \quad \text { or } \quad \bar{v}(\beta)=T \text { (or both), } \\ F & \text { otherwise. }\end{array}\right.$$
  4. $$\bar{v}((\alpha \rightarrow \beta))=\left\{\begin{array}{ll}F & \text { if } \bar{v}(\alpha)=T \text { and } \bar{v}(\beta)=F, \\ T & \text { otherwise. }\end{array}\right.$$
  5. $$\bar{v}((\alpha \leftrightarrow \beta))=\left\{\begin{array}{ll}T & \text { if } \quad \bar{v}(\alpha)=\bar{v}(\beta) \\ F & \text { otherwise. }\end{array}\right.$$

$\textbf{THEOREM 12A}$

For any truth assignment $v$ for a set $S$ there is a unique function

$$v : \bar \mS \to \{F, T\} $$ meeting the aforementioned conditions 0–5. --- $def:\textbf{Satisfy}$ A truth assignment $v$ *satisfies* a *wff* $\varphi$ iff. $\bar v(\varphi)=T$ > Of course for this to happen, the domain of $v$ must contain all sentence symbols in $\varphi$. --- $\textbf{DEFINITION: Tautologically Imply}$. Consider a set of *wff*s $\Sigma$ and another *wff* $\tau$. $\Sigma$ *tautologically implies* $\tau $ (written $\Sigma\vD\tau$ ) iff. every truth assignment for the sentence symbols in $\Sigma$ and $\tau $ that satisfies every member of $\Sigma$ also satisfies $\tau $ . > $\Sigma$ can be thought of as hypotheses and $\tau$ can be thought of as a possible conclusion. This definition reflects our intuitive feeling that a conclusion follows from a set of hypotheses if the assumption that the hypotheses are true guarantees that the conclusion is true. --- $def: \textbf{Tautology}$ consider a *wff* $\tau$, $\tau$ is a tautology iff. $\forall$ sentential symbol $\in\tau$, $\bar v(\tau)=T$. two special cases are that - $\forall \tau:\emptyset\vD \tau$ - $\forall \tau: \{A, \neg A\}\vD \tau$ > If no truth assignment satisfies every member of $\Sigma$, then for any $\tau $ , it is vacuously true that $\Sigma \vD \tau$ . --- $def:\textbf{Tautologically Equivalent}$ If $\Sigma$ is singleton $\{\sigma \}$, then we write "$\sigma\vD \tau $" in place of "$\{\sigma \} \vD \tau $". If both $\sigma \vD \tau $ and $\tau\vD \sigma$ , then $\sigma $ and $\tau $ are said to be *tautologically equivalent* (written $\sigma \te\tau$ ). # 3. A Parsing Algorithm The purpose of this section is to prove that we have used enough parentheses to eliminate any ambiguity in analyzing *wff*s. The existence of the extension $\bar v$ of a truth assignment $v$ will hinge on this lack of ambiguity. > 这一部分是证明 $\bar v$ 的存在性的 $\textbf{LEMMA 13A}$ Every *wff* has the same number of left as right parentheses. $\textbf{PROOF}$. The idea is that we start with sentence symbols (having zero left parentheses and zero right parentheses), and then apply formula-building operations which add parentheses only in matched pairs. We can rephrase this argument as follows: The set of <span class="bd-box"><h-char class="bd bd-end"><h-inner>“</h-inner></h-char></span>balanced<span class="bd-box"><h-char class="bd bd-beg"><h-inner>”</h-inner></h-char></span> wffs (having equal numbers of left and right parentheses) contains all sentence symbols and is closed under the formula-building operations. The ***[induction principle](#induction)*** then assures us that all *wff*s are balanced. --- $\textbf{LEMMA 13B}$ Any proper *initial segment* of a *wff* contains an excess of left parentheses. Thus no proper initial segment of a *wff* can itself be a *wff*. We are now going to describe a procedure that, given an expression, - both will determine whether or not the expression is a legal *wff*, - and if it is, will construct the tree showing how it was built up from sentence symbols by application of the formula-building operations. - Moreover, we will see that this tree is ***uniquely determined*** by the *wff*. # 4. Induction and Recursion ## 4.1. Induction >*Induction* is a special type of construction that occurs frequently both in logic and in other branches of mathematics. We may want to construct a certain subset $C$ of a set $U$ by starting with some initial elements of $U$, and applying certain operations to them over and over again. The set we seek ($C$) will be the **smallest set containing the initial elements and closed under the operations**. Its members will be those elements of $U$ which can be built up from the initial elements by applying the operations some finite number of times. In the special case of immediate interest to us, $U$ is the set of expressions, the initial elements are the sentence symbols, and the operations are $\mathcal E_{\neg}$, $\mE_{\land}$, etc. The set to be constructed is the set of *wff*s. But we will encounter other special cases later, and it will be helpful to view the situation abstractly here. To simplify our discussion, we will consider an initial set $B \subseteq U$ and a class $\mathcal F$ of functions containing just two members $f$ and $g$, where $$

f : U \times U \to U\ \text{ and }\ g : U → U
$$

Actually $\mathcal F$ need not be finite.

In defining the target subset $C$ more formally, we have our choice of two definitions.

  1. We can define it “from the top down” as follows:

    1. $def: \textbf{Closed}$

      Say that a subset $S$ of $U$ is closed under $f$ and $g$ iff whenever elements $x$ and $y$ belong to $S$, then so also do $f(x, y)$ and $g(x)$.

    2. $def: \textbf{Inductive}$

      Say that $S$ is inductive iff $B \subseteq S$ and $S$ is closed under $f$ and $g$.

      Let $C^*$ be the intersection of all the inductive subsets of $U$ ; thus $x ∈ C^*$ iff $x$ belongs to every inductive subset of $U$. It is not hard to see that $C^*$ is itself inductive. Furthermore, $C^*$ is the smallest such set, being included in all the other inductive sets.

  2. The second (and equivalent) definition works “from the bottom up.”

    We want $C_*$ to contain the things that can be reached from $B$ by applying $f$ and $g$ a finite number of times. Temporarily define a construction sequence to be a finite sequence $<span class="bd-box"><h-char class="bd bd-end"><h-inner>〈</h-inner></h-char></span>x_1, . . . , x_n<span class="bd-box"><h-char class="bd bd-beg"><h-inner>〉</h-inner></h-char></span>$ of elements of $U$ such that for each $i ≤ n$ we have at least one of

    $$\begin{array}{lll}x_{i} \in B & & \\ x_{i}=f\left(x_{j}, x_{k}\right) & \text { for some } & j<i, k<i \\ x_{i}=g\left(x_{j}\right) & \text { for some } & j<i\end{array} $$

    Then let $C_*$ be the set of all points $x$ such that some construction sequence ends with $x$. Let $C_n$ be the set of points $x$ such that some construction sequence of length $n$ ends with $x$. Then $C_1 = B$ and $\displaystyle C_* = \bigcup_n C_n$, where:

$$C_{1} \subseteq C_{2} \subseteq C_{3} \subseteq \cdots $$

At this point we should verify that our two definitions are actually equivalent, i.e., that $C^* = C_*$ .

  • $C^{*}\ {\subseteq}\ C_*$ : 由于 $C^*$ 是 $U$ 最小的归纳子集, 所以只要能证明到 $C_*$ is inductive.
  • $C_{*}\ {\subseteq}\ C^*$ :

4.2. Recursion

5. Sentential Connectives

cont.