Optimization and Search

1. Basic Knowledge of Maths

多元函数的 $\text{Taylor}$ Expansion

$${\displaystyle T(\boldsymbol {x} )=\sum _{|\alpha |\geq 0}{\frac {(\boldsymbol {x} -\boldsymbol {a} )^{\alpha }}{\alpha !}}\left({\mathrm {\partial } ^{\alpha }}f\right)(\boldsymbol {a} ),} $$

但是一般来说, 我们展开到二次就完全足够:

$${\displaystyle T(\boldsymbol {x} )=f(\boldsymbol {a} )+(\boldsymbol{x} -\boldsymbol {a} )^{\mathsf {T}}\nabla f(\boldsymbol {a} )+{\frac {1}{2!}}(\boldsymbol {x} -\boldsymbol {a} )^{\mathsf {T}}\left(\nabla^{2}f(\boldsymbol {a} )\right)(\boldsymbol {x} -\boldsymbol {a} )+\cdots ,} $$

where $\nabla f(\boldsymbol a)$ is the gradient of $f$ evaluated at $\boldsymbol x= \boldsymbol a$ and $\nabla ^2f(\boldsymbol a)$ is the Hessian matrix. 也就是说, 对于
$$

\boldsymbol x=\left{x_1, x_2, \ldots,x_n\right}

$$有: $$

\begin{align}
\nabla f(\boldsymbol x)=\frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}}=\left(\frac{\partial f_{1}(\boldsymbol{x})}{\partial x_{1}}, \frac{\partial f_{1}(\boldsymbol{x})}{\partial x_{2}}, \ldots, \frac{\partial f_{1}(\boldsymbol{x})}{\partial x_{n}}\right) \
\nabla^2f(\boldsymbol{x})=\frac{\partial}{\partial \boldsymbol{x}{i}} \frac{\partial f(\boldsymbol{x})}{\partial \boldsymbol{x}{j}}=\left(\begin{array}{cccc}\frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{1}^{2}} & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{1} \partial x_{n}} \ \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f(\boldsymbol{x})}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial f_{n}(\boldsymbol{x})}{\partial x_{n}^{2}}\end{array}\right)
\end{align}
$$

这里课件上的符号写的很随便. 我们假设这里的 $\nabla^2\not =\nabla\cdot \nabla=\Delta$ ($\text{Laplace}$ 算子), 而仅仅表示 $\text{Hessian}$ 矩阵

2. Gradient Descent

2.1. Principle

梯度下降法是典型的一阶优化算法. 梯度下降法的终极目标是: 如何在较少的次数下找出局部范围内偏导充分小的区域.

对于 $\boldsymbol x=\left\{x_1, x_2, \ldots,x_n\right\}\in \mathbb R$, 对于给定的初始点 $\boldsymbol x_0$ 以及定义在 $\mathbb R$ 上的函数 $f$, 我们定义梯度下降算法的过程如下:

$$\left.\begin{array}{rl} x_{1}^{(i+1)} & =x_{1}^{(i)}-\eta \cdot \displaystyle \frac{\partial f}{\partial x_{1}}\left(\boldsymbol{x}^{(i)}\right), \\ & \cdots \\ x_{n}^{(i+1)} & =x_{n}^{(i)}-\eta \cdot \displaystyle \frac{\partial f}{\partial x_{n}}\left(\boldsymbol{x}^{(i)}\right)\end{array}\right\}\iff \quad \boldsymbol{x}^{(i+1)}=\boldsymbol{x}^{(i)}-\eta \boldsymbol{\nabla} f(\boldsymbol{x}) $$

其中, $\eta$ 叫做学习率 ($\eta>0$)

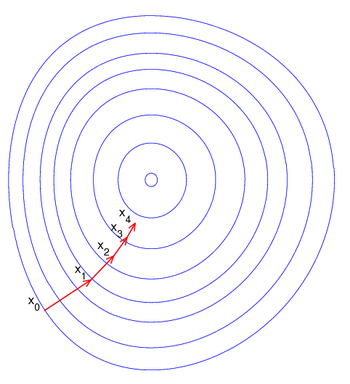
总的来说, 梯度下降法的过程包括四个部分:

• 目标函数定义
• 初始点选择
• 更新公式
• 结束机制

2.2. optimizations

我们发现上述的梯度下降法有失灵活性. 具体来说, 不管在函数的何种位置, 我们总是给予它相同程度的学习率. 历史上采取了多次优化

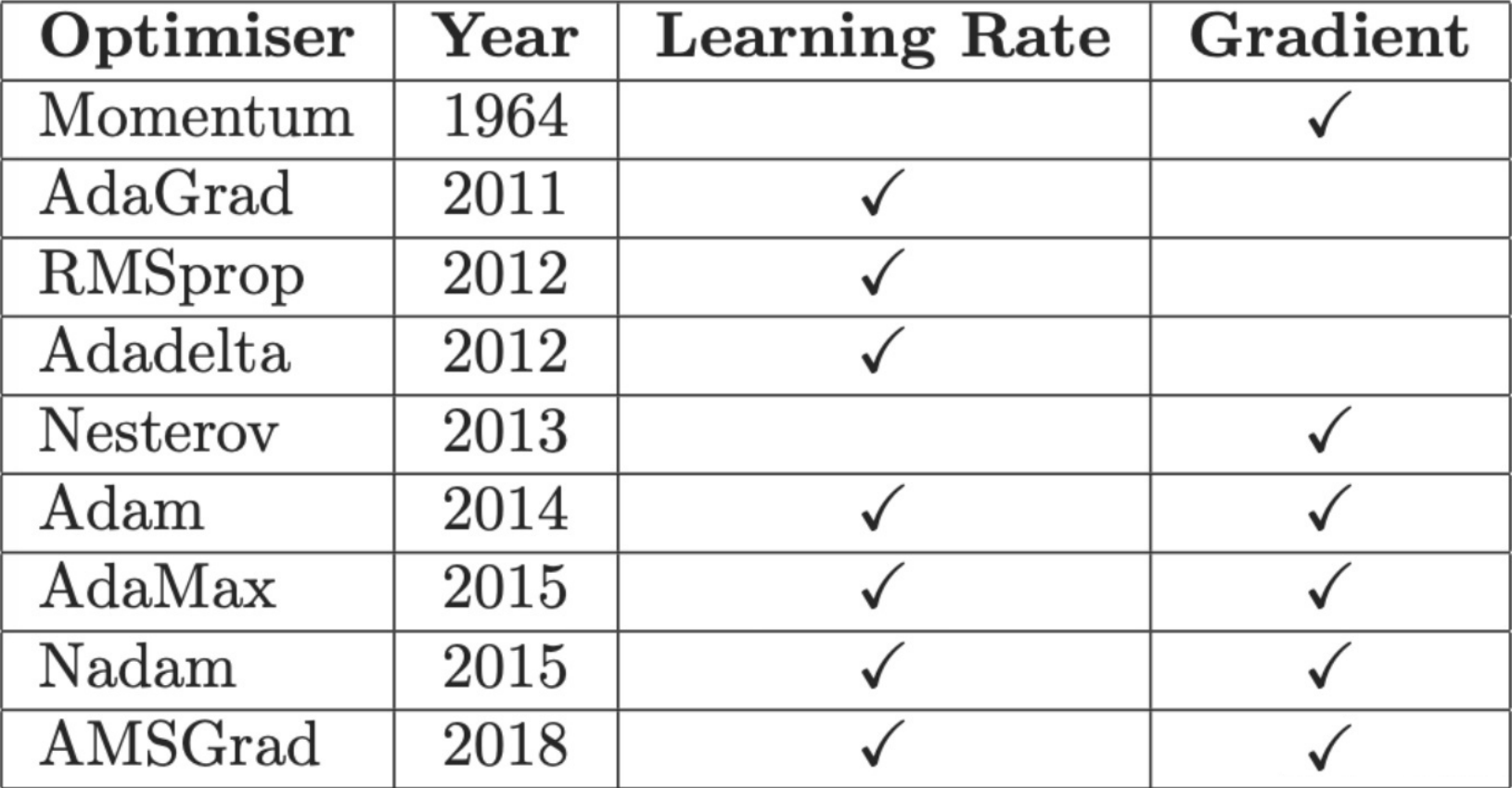
它们大致上可以分成如下的两类:

Learning Rate Schedulers (基于学习率的改进机制)

• 将学习率乘以一个常数或者时间因子, 使学习率能适应梯度. 当梯度值很大时, 希望更新小

Gradient Descent Optimizer (基于二阶梯度的改进机制)

• 将学习率乘以一个梯度的因子来进行调整
• 利用到之前的梯度来更好的指导梯度下降, 更近的梯度值获取更高的权重, 因而实现了exponential moving average

2.3. Representative Gradient Descent

Momentum

$$\left\{\begin{align} &W_{t+1}=W_{t}-\alpha V_{t} \\ &V_{t}=\beta V_{t-1}+(1-\beta) \displaystyle \frac{\partial L}{\partial W_{t}} \end{align}\right. $$

Nesterov Accelerated Gradient

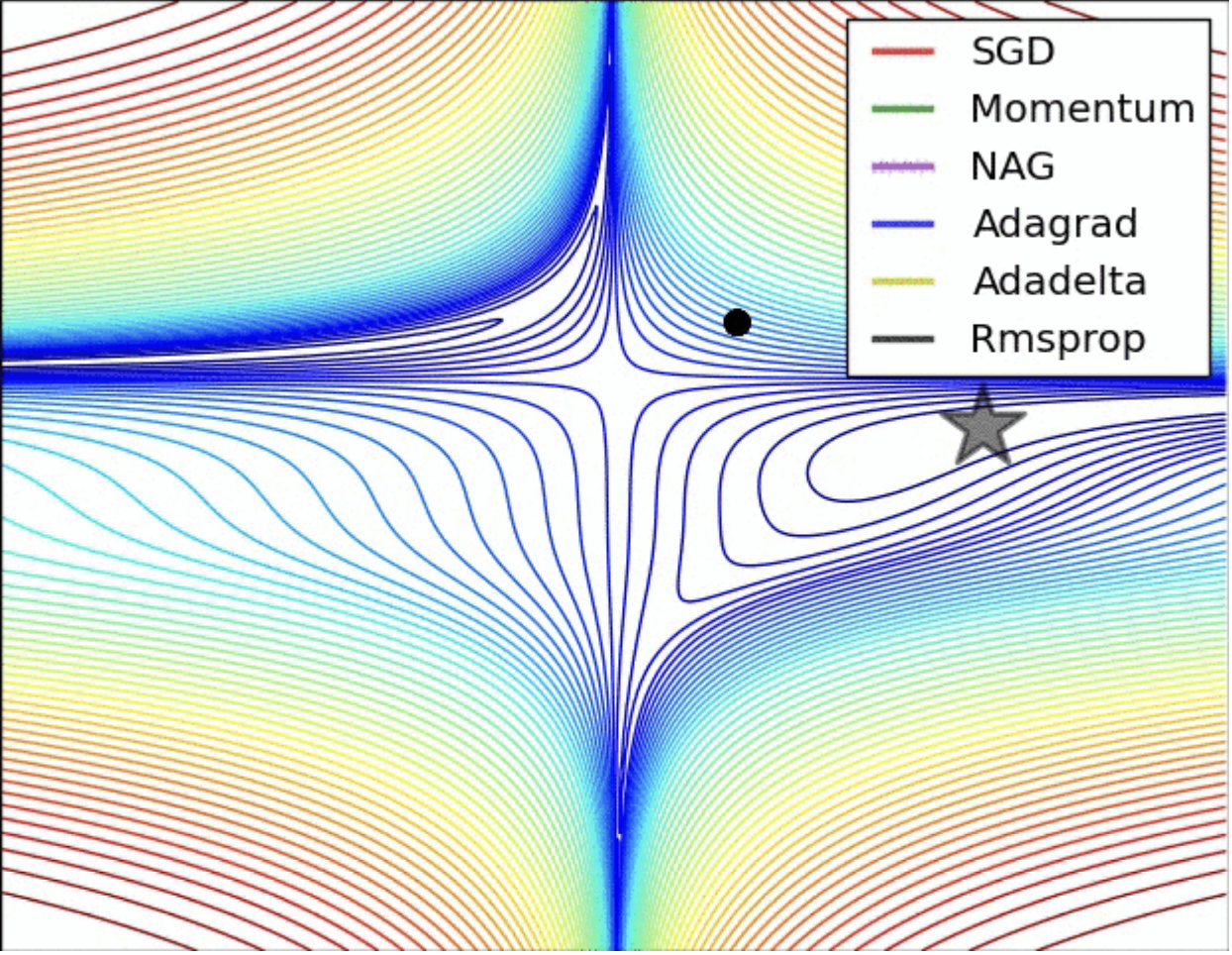
2.4. Limitations

梯度下降法被发现普遍存在下面的问题:

• 靠近极小值时收敛速度减慢
• 直线搜索时可能会产生一些问题
• 可能会“之字形”地下降

3. $\text{Newton}$'s Method

梯度下降法: 是一次平面去拟合当前点的局部曲面

牛顿法: 用二次曲面去拟合当前点的局部曲面

通常情况下: 二次曲面的拟合优于平面, 所以牛顿法选择的下降路径会更符合真实的最优下降路径.

3.1. Principle

$\text{Newton}$'s Method 同样是解决优化问题的方法. 一般来讲, 对于 $d\in\mathbb N$, $x\in\mathbb R^d$, 如果 $f$ 二次可微, 那我们忽略三阶及以上的高阶小量, 也就是注意到:

$${\displaystyle f(\boldsymbol {x+\boldsymbol x_0} ) \approx f(\boldsymbol {x}_0 )+{\boldsymbol x}^{\mathsf {T}}\nabla f(\boldsymbol x_0)+{\frac {1}{2!}}{\boldsymbol x}^{\mathsf {T}}\nabla ^{2}f(\boldsymbol x_0){\boldsymbol x}} $$

$\text{Newton}$'s Method 只不过令这里的 $\approx$ 变为 $=$, 并同时对 $\boldsymbol x$ 求偏导. 有:

$$\frac{\partial }{\partial \boldsymbol x_0}f(\boldsymbol x+\boldsymbol x_0)=\nabla f(\boldsymbol x_0)+\nabla ^2f(\boldsymbol x_0)\boldsymbol x_0 $$

最合适的 $\boldsymbol x_0$ 要能够使得 $\displaystyle \frac{\partial }{\partial \boldsymbol x_0}f(\boldsymbol x+\boldsymbol x_0)=0$, 也就是说

$$\begin {align} \boldsymbol x_0&=-{\left(\nabla ^2f(\boldsymbol x_0)\right)^{-1}}{\nabla f(\boldsymbol x_0)}\\ &=H^{-1}G \end {align} $$

需要计算海森矩阵的逆，计算复杂度为$O(n^3)$

我们注意到这里的 $\boldsymbol x_0$ 是向量, 因此 $\boldsymbol x_0$ 实际上刻画了下一步迭代前进的大小和方向.

3.2. Steps

1. 给定初始值 $\boldsymbol x_0$ 和精度阈值 $\varepsilon$, 并令 $k=0$
2. 计算 $\|\nabla f\|$, 如果 $\|\nabla f\|\le\varepsilon$, 终止迭代; 否则 $\Delta\boldsymbol x_k=-(\nabla ^2f(\boldsymbol x_k))^{-1}{\nabla f(\boldsymbol x_k)}$
3. 得到新的迭代点 $\boldsymbol x_{k+1}\leftarrow\boldsymbol x_k+\Delta \boldsymbol x_k$
4. 令$k\leftarrow k+1$, 转到第二步

3.3. Improvements

我们发现 $\text{Newton}$'s Method 在精度和效率两方面都可以提升. 对应地, 下面两种方法分别提升了精度和效率

1. Damped $\text{Newton}$ Method

对当前步长再做极小化优化.

考虑 $\lambda_{k}=\displaystyle \mathop{\operatorname {argmin}}\limits_{\lambda} f\left(\boldsymbol x_{k}+\lambda_{k} \Delta\boldsymbol x_0\right)$

1. 给定初始值 $\boldsymbol x_0$ 和精度阈值 $\varepsilon$, 并令 $k=0$
2. 计算 $\|\nabla f\|$, 如果 $\|\nabla f\|\le\varepsilon$, 终止迭代; 否则 $\Delta\boldsymbol x_k=-(\nabla ^2f(\boldsymbol x_k))^{-1}{\nabla f(\boldsymbol x_k)}$
3. 计算 $\lambda_k$, 得到新的迭代点 $\boldsymbol x_{k+1}\leftarrow\boldsymbol x_k+\lambda_k\Delta \boldsymbol x_k$
4. 令$k\leftarrow k+1$, 转到第二步

2. Quasi $\text{Newton}$ Method

$\text{Newton}$’ s Method 每一步都需要求解目标函数的 $H$ 矩阵的逆矩阵, 计算比较复杂. 并且要求目标函数必须二阶可导, $H$ 阵须正定. 这些要求都是非常严苛的. 为此我们设计了 Quasi $\text{Newton}$ Method

在拟牛顿法中, 我们用一个容易计算的矩阵 $\boldsymbol U$ 来模拟这个难以计算的 $\text{Hesse}$ 矩阵.

$${\displaystyle f(\boldsymbol {x+\boldsymbol x_0} ) \approx f(\boldsymbol {x}_0 )+{\boldsymbol x}^{\mathsf {T}}\nabla f(\boldsymbol x_0)+{\frac {1}{2}}{\boldsymbol x}^{\mathsf {T}}\boldsymbol U{\boldsymbol x}} $$

不同的拟牛顿法(DFP, BFGS, Broyden) 采用不同的计算方式

4. Conjugate Gradient

4.1. Principle

共轭梯度法是介于最速下降法与牛顿法之间的一个 方法, 它仅需利用一阶导数信息, 克服了最速下降法收敛慢的缺点, 又避免了牛顿法需要存储和计算 Hesse 矩阵并求逆的缺点.

在代数上, 两个向量 $\boldsymbol \alpha_i, \boldsymbol \alpha_j\in \mathbb R^d$ 共轭, 当且仅当存在半正定的 $A\in\mathbb R^{d\times d}$, 使得 $\boldsymbol \alpha_i^{\mathsf T} A\boldsymbol \alpha_j=0$. (这里的 $\boldsymbol \alpha_i, \boldsymbol \alpha_j$ 并不直接正交, 我们称它为 $A\text -$正交)

同样地,

$${\displaystyle f(\boldsymbol {x+\boldsymbol x_0} ) \approx f(\boldsymbol {x}_0 )+\boldsymbol x}^{\mathsf {T}}\nabla f(\boldsymbol x_0) $$

假设 $\boldsymbol x_k$ 是局部线性的, 则 $A\boldsymbol x=\boldsymbol b$:

$$\alpha_i=\frac{\boldsymbol p^{\mathsf T}_i\boldsymbol b}{\boldsymbol p^{\mathsf T}_i A\boldsymbol p_i}=\frac{\boldsymbol p^{\mathsf T}_i(-\nabla f(\boldsymbol x_{i-1}))}{p^{\mathsf T}_i A\boldsymbol p_i} $$

新的共轭方向的确定:

$$\boldsymbol p_k=\nabla f(\boldsymbol x_{k-1})+\sum_{i=0}^{k-1}\beta_{k_i}\boldsymbol p_i $$

$\text{Fletcher-Reeves}$ 公式:

$$\beta_{i+1}=\frac{\nabla f\left(\boldsymbol {x}_{i+1}\right)^{\mathsf T} \nabla f\left(\boldsymbol {x}_{i+1}\right)}{\nabla f\left(\boldsymbol {x}_{i}\right)^{\mathsf T} \nabla f\left(\boldsymbol {x}_{i}\right)} $$

$\text{Polak-Ribiere}$ 公式:

$$\beta_{i+1}=\frac{\nabla f\left({\boldsymbol x}_{i+1}\right)^{\mathsf T}\left(\nabla f\left({\boldsymbol x}_{i+1}\right)-\nabla f\left({\boldsymbol x}_{i}\right)\right)}{\nabla f\left(\boldsymbol {x}_{i}\right)^{\mathsf T} \nabla f\left(\boldsymbol {x}_{i}\right)} $$

4.2. Steps

1. 计算一个初始的搜索方向 $\boldsymbol p_0$ (利用梯度下降法)

2. 找一个使得目标函数 $f(\boldsymbol x_i +\alpha_i \boldsymbol p_i)$最小的 $\alpha_i$

3. 计算 $\boldsymbol x_{i+1}= \boldsymbol x_{i}+\alpha_i\boldsymbol p_i$

4. 确定下一个搜索方向 $\boldsymbol p_{i+1}=-\nabla f(\boldsymbol x_{i+1})+\beta_{i+1}\boldsymbol p_i$

   1. $\beta_{i+1}$ 由前一个迭代点梯度 $\nabla f(\boldsymbol x_i)$, 当前迭代点梯度 $\nabla f(x_{i+1})$ 共同决定
   2. 迭代完所有共轭方向

5. 如不满足终止条件, 则回到第一步, 继续确定新的第一个梯度方向

5. Least Squares Method

假设 $\boldsymbol r\left(\boldsymbol x)=(r_1(\boldsymbol x),r_2(\boldsymbol x),\ldots,r_m(\boldsymbol x)\right)^{\mathsf T}$, $\boldsymbol J(\boldsymbol x)=\left[\displaystyle \frac{\partial r_j}{\partial x_i}\right]$, $j=1,2,\ldots,m;i=1,2,\ldots,n$.

最小二乘法的目标函数为

$$f(\boldsymbol x)=\displaystyle\frac{1}{2}\sum_{i=1}^mr_i(\boldsymbol x)^2={1\over 2}\|\boldsymbol r(\boldsymbol x)\|^2 $$

不难发现

$$\begin {array} \displaystyle \nabla f(\boldsymbol x)=\boldsymbol J^{\mathsf T}(\boldsymbol x)\boldsymbol r(\boldsymbol x)\\ \displaystyle \nabla^2 f(\boldsymbol x)=\boldsymbol J^{\mathsf T}(\boldsymbol x)\boldsymbol J(\boldsymbol x)+\sum_{j=1}^{m}r_j(\boldsymbol x)\nabla^2 r_j(\boldsymbol x) \end {array} $$

to be continued…