Interpolation Problems

$$\huge\textbf{Interpolation Problems} $$

1. 一维插值问题

已经有 $n+1$ 个节点 $(x_i, y_i)(i=0,1,2,...,n)$, 其中 $x_i$ 互不相同. 不妨假设 $x_i<x_{i+1}(i=0,1,2,...,n-1)$, 求任一插值点 $x^*(\not=x_i)$ 处的估计值 $y^*$.

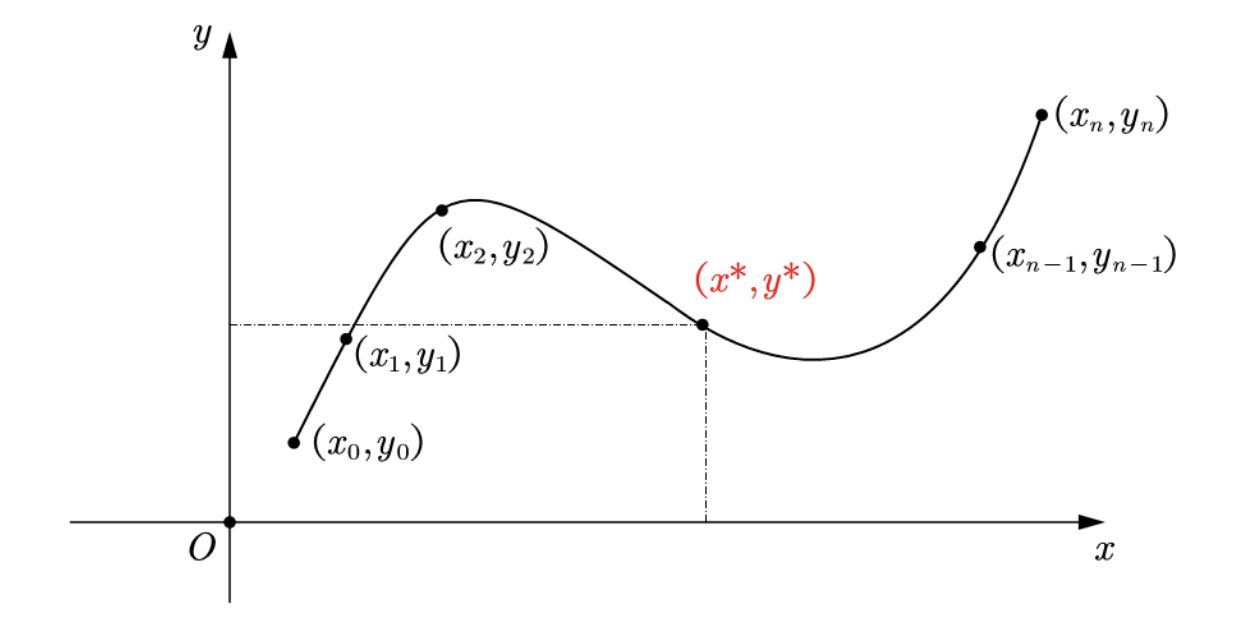
我们很自然地考虑用一个不太复杂的函数 $f$ 来估计这 $n$ 个点——即这个函数要经过它们全部的点. 这样 $y^*=f(x^*)$

这样的问题叫做一维插值问题, $x_i(i=0,1,2,...,n)$ 为插值节点, $[x_0, x_n]$ 为插值区间 (根据假设). 这样的方法叫做插值法. 有很多常见的插值方法: 多项式插值, 分段插值, 三角插值…

2. 一般多项式插值

2.1. Principle

一个自然的问题是, 插值多项式在什么情况下是唯一的. 实际上, 假设有 $n+1$ 个节点 $(x_i, y_i)(i=0,1,2,...,n)$, 其中 $x_i$ 互不相同. 不妨假设 $x_i<x_{i+1}(i=0,1,2,...,n-1)$, 那么存在唯一的多项式

$$L_n(x)=a_0+\sum_{i=1}^na_ix^i $$

使得 $L_n(x_i)=y_i(i=0,1,2,...,n)$

给出证明如下: 令

$$A=\left[\begin{array}{cccc}1 & x_{0} & \cdots & x_{0}^{n} \\ 1 & x_{1} & \cdots & x_{1}^{n} \\ \vdots & \vdots & \cdots & \vdots \\ 1 & x_{n} & \cdots & x_{n}^{n}\end{array}\right] \quad X=\left[\begin{array}{c}a_{0} \\ a_{1} \\ \vdots \\ a_{n}\end{array}\right] \quad Y=\left[\begin{array}{c}y_{0} \\ y_{1} \\ \vdots \\ y_{n}\end{array}\right] $$

那么问题就变成了传统的 $AX=Y$ 的问题.

而 $A$ 作为 $\text{Vandermonde}$ 矩阵, 容易发现 $\det(A)=\displaystyle\prod_{0\leq i< j\le n}(x_j-x_i)\not =0$, 所以方程组 $AX=Y$ 有唯一解为:

$$X=A^{-1}Y $$

但很明显, 如果多项式的次数更高, 则结果不一定唯一.

2.2. $\text{Lagrange}$ 插值

上面的原理只证明了存在性, 但是 $\text{Lagrange}$ 插值多项式则是构造性地阐明了如何确定多项式的系数.

这里的系数 $a_i$ 应该是关于 $x_i$ 和 $y_i$ 的函数. 我们假设

$$L_n(x)=\sum_{i=0}^n l_i(x)y_i $$

其中 $l_i(x)=\text{sig} (x==x_i)$. 如果你代数还不错可以进行如下的构造:

$$L_n(x)=\sum_{i=0}^n\left(\displaystyle\prod_{i\not=k}\frac{(x-x_i)}{(x_k-x_i)}\right)y_k $$

很妙.

2.3. $\text{Runge}$ 现象

很自然地, 我们会以为, 插值次数越高, 对原函数的逼近可能就越精确. 但是 $\text{Runge}$ 现象否定了我们的猜想.

考虑以下 $\text{Runge}$ 函数：

$$f(x) = \frac{1}{1+x^2} $$

龙格发现如果使用 $\leq n$ 阶多项式 $P_n(x)$ 在 $-1$ 与 $1$ 之间按照

$$x_i = -1 + (i-1)\frac{2}{n},\qquad i \in \left\{ 1, 2, \dots, n+1 \right\} $$

这样的等距点 $x_i$ 进行插值, 那么在接近端点 $-1$ 与 $1$ 的地方插值结果就会出现震荡.

可以证明, 在多项式的阶数增高时插值误差甚至会趋向无限大：

$$\lim_{n \rightarrow \infty} \left( \max_{-1 \leq x \leq 1} | f(x) -P_n(x)| \right) = \infty $$

根据维基百科的描述, 要缓解 $\text{Runge}$ 现象, 可以使用 $\text{Chebyshev}$ 节点.

3. 分段插值

3.1. 分段二次插值

在上面提出的 $\text{Runge}$ 现象告诉我们, 提高次数不能提高精确性. 一种朴素的解决方式是, 采用分段低次插值. 可以选取和节点 $x$ 最近的三个节点 $x_{i-1}, x_i,x_{i+1}$, 进行二次插值, 也就是在每一个 $[x_{i-1},x_{i+1}]$ 上, 采用如下的插值:

$$f(x) \approx L_{2}(x)=\sum_{k=i-1}^{i+1}\left( \prod_{\substack{j=i-1 \\ j \neq k}}^{i+1} \frac{\left(x-x_{j}\right)}{\left(x_{k}-x_{j}\right) }\right)y_{k} $$

这样的插值方法叫做分段二次插值.

3.2. $\text{Newton}$ 插值

我们发现 $\text{Lagrange}$ 插值法的可修改性比较差, 也即, 如果添加一个点, 所有的系数要重新计算. 但是 $\text{Newton}$ 插值法没有这样的问题.

$\text{Newton}$ 多项式 $N_{n+1}(x):=f(x)$, 其中 $f(x)$ 有如下的定义.

$$\begin{aligned} f(x)= & f\left(x_{0}\right)+f\left[x_{0}, x_{1}\right]\left(x-x_{0}\right) \\ & +f\left[x_{0}, x_{1}, x_{2}\right]\left(x-x_{0}\right)\left(x-x_{1}\right)+\cdots \\ & +f\left[x_{0}, x_{1}, \cdots, x_{n-2}, x_{n-1}\right]\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{n-3}\right)\left(x-x_{n-2}\right) \\ & +f\left[x_{0}, x_{1}, \cdots, x_{n-1}, x_{n}\right]\left(x-x_{0}\right)\left(x-x_{1}\right) \cdots\left(x-x_{n-2}\right)\left(x-x_{n-1}\right)\end{aligned} $$

其中, $f[x_0,x_1,\ldots,x_k]$ 称为 $f$ 关于点 $x_0,x_1,\ldots,x_k$ 的 $k$ 阶差商. 我们给出它的递归定义:

$$f\left[x_{0}, x_{1}, \ldots, x_{k}\right]:=\frac{f\left[x_{1}, \ldots x_{k-1}, x_{k}\right]-f\left[x_{0}, x_{1}, \ldots x_{k-1}\right]}{x_{k}-x_{0}} $$

但实际上, $\text{Newton}$ 插值法仍然存在 $\text{Runge}$ 现象.

4. 更加精细的插值

4.1. 前两种插值的缺陷

上面讲的两种插值仅仅要求插值多项式在插值节点处与被插函数有相等的函数值, 而这种插值多项式却不能全面反映被插值函数的性态. 然而在许多实际问题中, 不仅要求插值函数与被插值函数在所有节 点处有相同的函数值, 它也需要在一个或全部节点上插值多项式与被插 函数有相同的低阶甚至高阶的导数值. 对于这些情况, $\text{Lagrange}$ 插值和 $\text{Newton}$ 插值都不能满足.

4.2. $\text{Hermite}$ 插值

$f(x)$ 在区间 $[a,b]$ 上有 $n+1$ 个互异节点, $a=x_{0}<x_{1}<x_{2}<\ldots<x_{n}=b$. 定义在 $[a, b]$ 上的函数 $f(x)$ 在节点上满足:

$$f\left(x_{i}\right)=y_{i}, f^{\prime}\left(x_{i}\right)=y_{i}^{\prime}(i=0,1,2, \ldots n) $$

这样 $2n+2$ 个条件. 那么可以唯一确定一个次数不超过 $2n+1$ 的多项式 $H_{2n+1}(x)=H(x)$ 满足:

$$H\left(x_{j}\right)=y_{j}, \quad H^{\prime}\left(x_{j}\right)=m_{j} \quad(j=0,1, \cdots n) . $$

其余项为:

$$R(x)=f(x)-H(x)=\frac{f^{(2 n+2)}(\xi)}{(2 n+2) !} \omega_{2 n+2}(x) $$

4.3. $\text{PCHIP}$

直接使用Hermite插值得到的多项式次数较高, 也存在着 $\text{Runge}$ 现象, 因此在实际应用中, 往往使用分段三次 $\text{Hermite}$ 插值多项式 ($\text{PCHIP}$: Piecewise Cubic Hermite Interpolating Polynomial).

想法和上面的分段一样. 实现上直接调包即可.

4.4. 三次样条插值

不难发现 $\text{PCHIP}$ 虽然好, 但是在节点处只有一阶可微. 但是我们希望把握函数的凹凸性来更好地进行预测. 因此我们考虑一种更加精细的插值: 三次样条插值 ($\text{cubic spline}$).

$f(x)$ 在区间 $[a,b]$ 上有 $n+1$ 个互异节点, $a=x_{0}<x_{1}<x_{2}<\ldots<x_{n}=b$. 定义在 $[a, b]$ 上的函数 $f(x)$ 在节点上满足:

(1) $S(x_i)=f\left(x_{i}\right)=y_{i}(i=0,1,2, \ldots n)$

(2) 在每个子区间 $[x_i,x_{i+1}]$ 上 $S(x)$ 为三次多项式.

(3) $S(x)$ 在 $[a,b]$ 上二阶连续可微

因此我们希望 $S(x)$ 要满足如下的几个条件:

$$S(x)=\left\{\begin{array}{ll}S_{0}(x), & x \in\left[x_{0}, x_{1}\right], \\ S_{1}(x), & x \in\left[x_{1}, x_{2}\right], \\ & \vdots \\ S_{n-1}(x), & x \in\left[x_{n-1}, x_{n}\right] ;\end{array}\right. $$

$$\left\{\begin{array}{l}S_{i-1}\left(x_{i}\right)=S_{i}\left(x_{i}\right) \\ S_{i-1}^{\prime}\left(x_{i}\right)=S_{i}^{\prime}\left(x_{i}\right) \\ S_{i-1}^{\prime \prime}\left(x_{i}\right)=S_{i}^{\prime \prime}\left(x_{i}\right)\end{array}\right. $$

同样在实现上调包即可.

5. 三角插值

这一部分很大程度上参考了这篇文章

三角插值由于其形式的特殊性, 一般要用到 $\text{Fourier}$ 分析等手段.

5.1. 一般意义上的三角插值

假设我们有一个函数 $f(t)$ , 假设它的周期是 $2\pi$ . 我们知道它在一些点处的函数值, 我们想用三角插值的方法去近似它. 那么, 我们可以构造一个 $n$ 阶三角多项式:

$$p_{n}(x)=a_{0}+\sum_{j=1}^{n} a_{j} \cos (j t)+\sum_{j=1}^{n} b_{j} \sin (j t) $$

因为这个三角多项式中有 $2n+1$ 个待定系数, 所以我们需要 $2n+1$ 个数据点才能确定这个插值多项式.

一般来说，我们通常会认为 $p_n(x)$ 是一个复变量的函数, 这样在理解三角多项式的一些性质时会带来方便. 当然, 结论对于实变量的情况也应该成立. 根据 $\text{Euler}$ 公式:

$$\cos x=\frac{e^{i x}+e^{-i x}}{2}, \quad \sin x=\frac{e^{i x}-e^{-i x}}{2 i} $$

我们便有:

$$\begin{aligned} p_{n}(x) & =a_{0}+\sum_{j=1}^{n} a_{j} \frac{e^{i j t}+e^{-i j t}}{2}+\sum_{j=1}^{n} b_{j} \frac{e^{i j t}-e^{-i j t}}{2 i} \\ & =a_{0}+\sum_{j=1}^{n} \frac{a_{j}-i b_{j}}{2} e^{i j t}+\frac{a_{j}+i b_{j}}{2} e^{-i j t} \\ & =\sum_{j=-n}^{n} c_{j} z^{j}\end{aligned} $$

其中:

$$c_{0}=a_{0}, c_{j}=\frac{a_{j}-i b_{j}}{2}, c_{-j}=\frac{a_{j}+i b_{j}}{2}, \quad j=1,2, \ldots, n ; z=e^{i .} $$

这样我们就把 $p_n(x)$ 写成了一个类似多项式的形式. 事实上, 如果我们考虑一个多项式 $\tilde{p}_{n}(x)=\displaystyle\sum_{j=-n}^{n} c_{j} x^{j}$ ，并且记 $z_{l}=e^{i t_{l}}$ 的话，那么满足下面条件的多项式 $\tilde{p}_{n}\left(z_{l}\right)$ 的系数 $c_j$ 就是我们要找的三角多项式的系数:

$$\tilde{p}_{n}\left(z_{l}\right)=f\left(t_{l}\right), \quad l=0,1,2, \ldots, 2 n $$

至此, 我们就把三角多项式插值的问题转化为了一般的多项式插值问题, 根据上面的 $\text{Lagrange}$ 插值方法, 三角多项式的系数是存在且唯一的.