Multiple Linear Regressive Analysis

1. Intro to Multiple Linear Regression

回归分析是数据分析中最基础也是最重要的分析工具, 绝大多数的 数据分析问题, 都可以使用回归的思想来解决. 回归分析的任务就是, 通过研究自变量 $X$ 和因变量 $Y$ 的相关关系, 尝试去解释 $Y$ 的形成机制, 进而达到通过 $X$ 去预测 $Y$ 的目的. 常见的回归分析有几类:

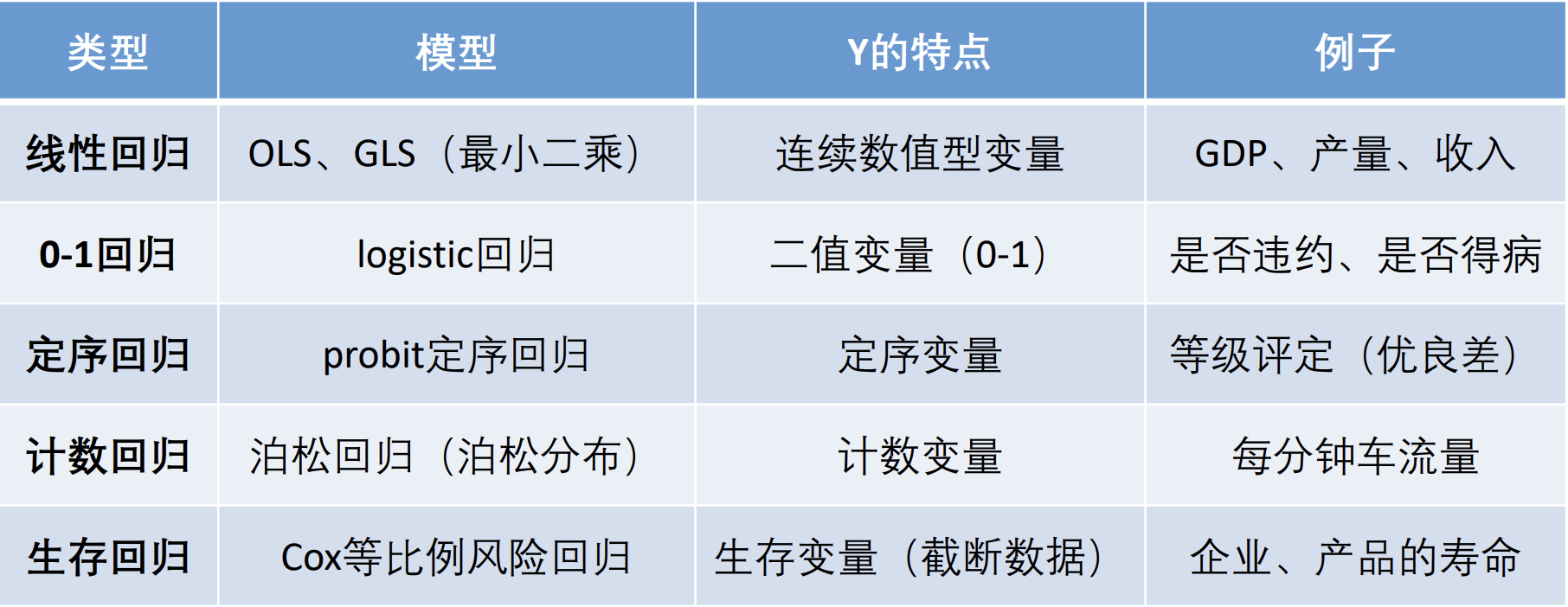
其划分的依据是因变量 $Y$ 的类型. 在这里我们主要研究线性回归.

对于相关性, 我们要明确: 相关性 $\not=$ 因果性. 在绝大多数情况下, 我们没有能力去探究严格的因果关系, 所以只好退而求其次, 改成通过回归分析, 研究相关关系. 而一个相关问题的解决, 需要面对三个不可避免的问题:

• 识别重要变量: 回归分析要去识别并判断: 哪些X变量是同Y真的相关, 哪些不是. 统计学中有一个非常重要的领域, 叫做变量选择.
• 判断相关性的方向: 去除了那些同 $Y$ 不相关的 $X$ 变量, 剩下的就都是重要的 $X$ 变量了. 接下来回归分析要回答的问题是: 这些有用的X变量同Y的相关关系是正的还是负的
• 估计权重: 在确定了重要的 $X$ 变量的前提下, 我们还想赋予不同 $X$ 不同的权重, 也就是不同的回归系数, 进而我们可以知道不同变量之间的相对重要性.

2. Linear Regressive Analysis

2.1. 数据的获取

一般来说, 数据分析问题中的数据可以分成如下三类

• 横截面数据: 在某一时点收集的不同对象的数据.
• 时间序列数据: 对同一对象在不同时间连续观察所取得的数据. (重点看后面的Time Series Analysis)
• 面板数据: 横截面数据与时间序列数据综合起来的一种数据资源.

其中, 最适合使用回归分析进行建模的是横截面数据. 时间序列数据往往要进行时间序列分析, 对数据进行一定程度的预测. 面板数据较为复杂, 是中级计量经济学中使用到的模型.

2.2. Linear Regression

这一部分在笔者数据科学笔记中的回归分析部分中有相对详细的记录

3. Improvements

3.1. Drawbacks of OLS

OLS 回归中关于自变量的选择大有门道, 变量过多时可能会导致多重共线性问题造成回归系数的不显著, 甚至造成OLS估计的失效. 我们将介绍两种新的回归: 岭回归和lasso回归. 它们各自在 OLS 回归模型的损失函数上加上了不同的惩罚项, 该惩罚项由回归系数的函数构成, 一方面, 加入的惩罚项能够识别出模型中不重要的变量, 对模型起到简化作用, 可以看作逐步回归法的升级版; 另一方面, 加入的惩罚项能够让模型变得可估计, 即使之前的数据不满足列满秩, 在稍后的原理推导中我们将更加详细的说明这一点.

3.2. $\text{Ridge}$ Regression

岭回归 (Ridge regression: Hoerl and Kennard, 1970) 的原理和 OLS 估计类似, 但是对系数的大小设置了惩罚项.

对于模型 $y=\beta_0 + \displaystyle \sum_{i=1}^{m-1}\beta_ix_i + \mu$,

多元线性回归

$$\hat \beta =\displaystyle \arg\min_{\hat\beta}\sum_{i=1}^n(y_i-x_i^T\hat\beta)^2\quad\hat\beta =\left(\hat\beta_1, \hat\beta_2,\ldots,\hat\beta_n\right) $$

$\text{Ridge}$回归:

$$\begin{aligned}\hat \beta &=\displaystyle \arg\min_{\hat\beta}\left[\sum_{i=1}^n(y_i-x_i^T\hat\beta)^2+\lambda\sum_{i=1}^n\hat\beta_i^2\right]\\&=\arg\min_{\hat\beta}\left[(y-x\hat\beta)^T(y-x\hat\beta)+\lambda\hat\beta^T\hat\beta\right]\end{aligned} $$

其中 $\hat\beta =\left(\hat\beta_1, \hat\beta_2,\ldots,\hat\beta_n\right)$, 不难发现, $\hat\beta=(x^Tx+\lambda I)^{-1}x^Ty \quad\lambda>0$

3.3. $\text{LASSO}$ Regression

least absolute shrinkage and selection operator

最初由斯坦福大学统计学教授罗伯特·蒂布希拉尼于1996年基于Leo Breiman的非负参数推断(Nonnegative Garrote, NNG)提出. Lasso算法最初用于计算最小二乘法模型，这个简单的算法揭示了很多估计量的重要性质，如估计量与岭回归（Ridge regression，也叫吉洪诺夫正则化）和最佳子集选择的关系，Lasso系数估计值(estimate)和软阈值（soft thresholding）之间的联系。它也揭示了当协变量共线时，Lasso系数估计值不一定唯一（类似标准线性回归）. 在形式上, $\text{LASSO}$ 回归与岭回归类似.

$\text{LASSO}$ 回归:

$$\begin{aligned}\hat \beta &=\displaystyle \arg\min_{\hat\beta}\left[\sum_{i=1}^n(y_i-x_i^T\hat\beta)^2+\lambda\sum_{i=1}^n|\hat\beta_i|^2\right]\\\end{aligned} $$

缺点是: $\text{LASSO}$ 回归没有代数解, 只能数值估计.