CS►Data Science

10. Linear Regressive Analysis

$$\huge\textbf{Linear Regressive Analysis} $$

1. Unary Linear Regressive Analysis

1.1. Basic Steps

采集样本 $\to$ 回归分析 $\to$ 对回归方程显著性检验 $\to$ 预测与控制

1.2. Ordinary Least Squares Estimation (OLS)

称 $y = a+bx+e$ 为一元线性回归方程，其中 $a+bx$ 表示 $y$ 随 $x$ 线性变化的部分，$e$ 是一切随机因素的总和，要使得这一误差最小，考察

$$y_i=a+bx_i+e_i $$

令

$$Q(a,b)=\sum_{i=1}^ne_i^2=\sum_{i=1}^n(a+bx_i-y_i)^2 $$

根据微分方程极值原理，令

$$\left\{ \begin{array}{**lr} \displaystyle\frac{\partial Q}{\partial a}=-2\sum_{i=1}^n(y_i-a-bx_i)=0\\ \displaystyle\frac{\partial Q}{\partial b}=-2\sum_{i=1}^nx_i(y_i-a-bx_i)=0\\ \end{array} \right. $$

解得

$$\left\{ \begin{array}{**lr} \hat a=\overline y-\hat b\\ \displaystyle \hat b=\frac{l_{xy}}{l_{xx}} \end{array} \right. $$

其中

$$\left\{ \begin{array}{**lr} l_{xy}=\displaystyle \sum_{i=1}^n(x_i-\overline x)(y_i-\overline y)=\sum_{i=1}^nx_iy_i-\frac{1}{n}(\sum_{i=1}^ny_i)(\sum_{i=1}^nx_i) \\l_{xx}=\displaystyle \sum_{i=1}^n(x_i-\overline x)^2=\sum_{i=1}^nx_i^2-\frac{1}{n}(\sum_{i=1}^nx_i)^2 \end{array} \right. $$

同时，我们用

$$r^2=\frac{S_R}{S_T} $$

表示回归直线对样本的拟合程度 ($|r|$ 越接近1, 拟合程度越高), 或者可以用残差 (开根号后为标准残差) 来表示偏差累计:

$$S_y^2=\frac{S_e}{n-2}=\frac{\displaystyle \sum_i(y_i-\hat y_i)^2}{n-2} $$

1.3. Significance Test

我们发现, 上文的最小二乘估计中少了一个关键的步骤: 查看样本数据的相关性. 实际上, 如果对一组毫不相关的数据进行最小二乘估计, 得到一个 $\text{Pearson}$ 系数几乎为 0 的回归方程, 是没有意义的. 为了进行高效的回归, 我们引入如下的几个变量, 进行所谓显著性检验.

$def$: 总偏差平方和 $S_T$:

$$S_T:=\sum_{i=1}^n(y_i-\overline y)^2 $$

$def$: 回归偏差平方和 $S_R$

$$S_R:=\sum_{i=1}^n(\hat y_i-\overline y)^2 $$

$def$: 随机误差 $S_e$:

$$S_e:=\sum_{i=1}^n(y_i-\hat y_i)^2 $$

$Thm$: 一元线性回归分析中，总偏差平方和等于回归偏差平方和与随机误差之和，即：

$$S_T=S_R+S_e $$

证明也比较 trivial, 全部展开即可.

1.4. Prediction and Control

我们根据样本数据建立一元线性回归方程 $y=\hat a+\hat bx$, 此时我们可以根据给定的 $x_0$ 来预测 $y_0$ 的取值. 这样的预测可以分成两类:

点预测: $\hat y_0=\hat a+\hat bx_0$

区间预测: 由于不同样本的估计的 $a,b$ 值可能不同, 所以 $\hat y_0$ 与 $y_0$ 可能存在抽样误差. 可以证明:

$$\left(\hat{y}_{0}-y_{0}\right) \sim N\left(0, \sigma^{2}\left[1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{\sum\left(x_{i}-\bar{x}\right)^{2}}\right]\right) $$

因此, $y_0$ 的置信度为 $1-\alpha$ 的预测区间为:

$$\hat{y}_{0} \pm t_{\alpha / 2}(n-2) \sigma \sqrt{1+\frac{1}{n}+\frac{\left(x_{0}-\bar{x}\right)^{2}}{\sum\left(x_{i}-\bar{x}\right)^{2}}} $$

因此当 $x_0$ 在 $\bar x$ 附近, $n$ 充分大时, 可以近似地认为 $(\hat y_0-y_0)\sim \mathbb N(0, S_y^2)$. 因此 $y_0$ 的概率为 $1-\alpha$ 的置信区间为:

$$y_0\pm t_{\alpha / 2}(n-2)S_y $$

2. Multiple Linear Regressive Analysis

实际应用中, 如果因变量和自变量为多个数据的组合, 那么我们使用一元回归分析是难以开展的. 在回归分析中, 如果自变量有2个或2个以上时, 称为多元回归分析.

2.1. Basic Steps

考察因变量 $y$ 与 $m-1$ 个自变量 $x_1,x_2,…,x_{m-1}$ 的关系, 分析如下的多元线性回归模型, 即:

$$y=\beta_0 + \sum_{i=1}^{m-1}\beta_ix_i + \mu $$

为了方便, 采用以下记号：

$$Y= \left[ \begin{array}{} y_1\\ y_2\\ \ \vdots\\ y_n \end{array} \right], \beta= \left[ \begin{array}{} \beta_0\\ \beta_1\\ \ \vdots\\ \beta_{m-1} \end{array} \right], \mu= \left[ \begin{array}{} \mu_1\\ \mu_2\\ \ \vdots\\ \mu_n \end{array} \right], X= \left[ \begin{array}{} 1 & x_{11} & \cdots & x_{1(m-1)}\\ 1 & x_{21} & \cdots & x_{2(m-1)}\\ \ \vdots & \vdots & \vdots & \vdots\\ 1 & x_{n1} & \cdots & x_{n(m-1)} \end{array} \right] $$

则多元线性回归模型 $(Y,X\beta,\sigma^2I_n)$ 可简化为

$$\left\{ \begin{array}{**lr} Y= X\beta + \mu\\ e\sim\mathbb{N}(0,\sigma^2I_n) \end{array} \right. $$

则相应地,

$$\begin{align} \hat\beta &=(X^TX)^{-1}X^TY\\ \mu &=Y-\hat Y=(I-H)Y\\ S_T &=Y^TY-\frac{1}{n}Y^TJY\\ S_{\mu} &=Y^TY-\hat\beta X^TY\\ S_R &=S_T-S_\mu\\ r^2 &=\frac{S_R}{S_T} \end{align} $$

2.2. Partial Regression Coefficient Analysis

偏回归系数指的就是多元回归模型中的回归系数, 因为根据定义, $\hat\beta_m=\displaystyle\frac{\partial y_i}{\partial x_{mi}}$

回归关系显著并不意味着每个自变量 $x_j$ 对 $y$ 的影响都显著. 若 $x_j$ 对 $y$ 无影响, 那么线性方程中对应的 $\beta_j=0$. 我们对每个自变量进行以下假设检验:

$$H_0: \beta_j=0\\ H_1:\beta_j\not =0 $$

我们需要计算检验统计量：

$$\frac{\hat\beta_j-\beta_j}{S(\hat\beta_j)}\sim t(n-m) $$

所以, $\beta_j$ 的 $1-\alpha$ 置信区间为

$$\hat\beta_j\pm t_{\alpha\over 2}(n-m)S(\hat\beta_j) $$

2.3. Endogeneity

内生性

假设我们的模型为 $y=\beta_0+\displaystyle\sum_{i=0}^k\beta_ix_i+\mu$, 其中 $\mu$ 为无法观测并且满足一定条件的扰动项. 如果误差 $\mu$ 满足与所有的自变量 $x_i$ 均不相关, 那么称该回归模型具有外生性. 否则称该回归模型具有内生性. 内生性会导致回归系数估计的不准确: 不满足无偏和一致性.

简单来说: 包含了所有与 $y$ 相关, 但未添加到回归模型中的变量, 如果这些变量和我们已经添加的自变量相关, 则存在内生性.

一个例子是, 对于实际的模型 $y=0.5+2x_1+5x_2+\mu,mu\sim\mathbb N(0,1)$, 如果 $x_1$ 在 $[-10,10]$ 上均匀分布, 并且如果我们用一元线性回归模型 $y=kx_1+b+\mu'$, 那么使用 $\text{Monte Carlo}$ 模拟可以发现, 估计出来的 $k$ 的大小与 $\rho_{x_1,\mu'}$ 有如下图的关系.

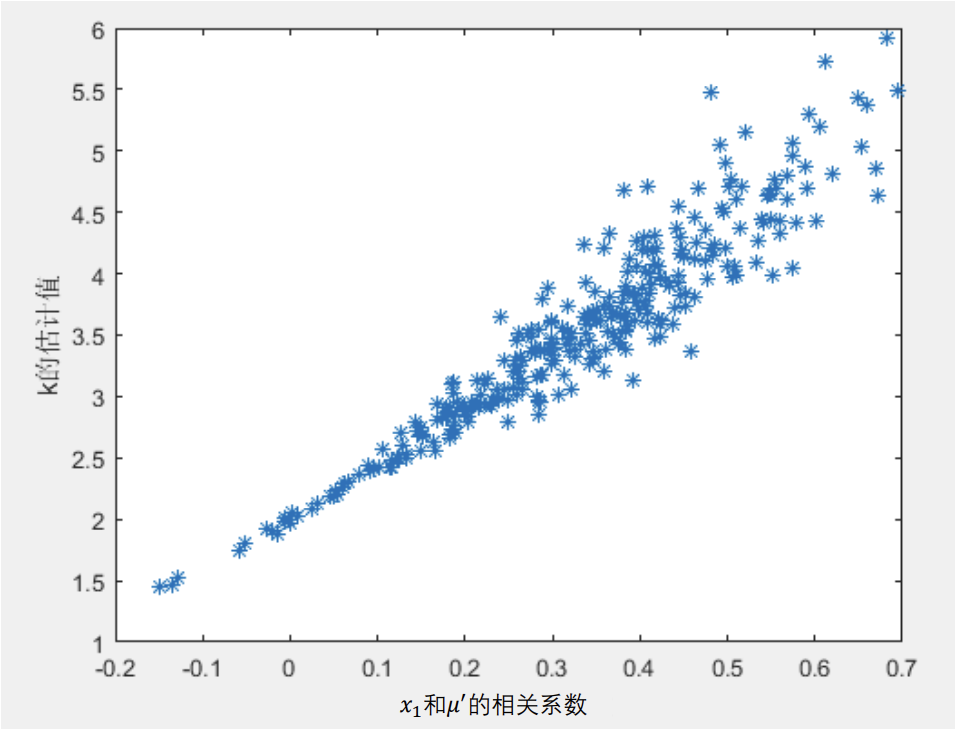
内生性难以避免, 因为为解释变量一般很多 (5‐15个). 在实践中, 我们大可以采用如下的方法来弱化内生性: 将解释变量分成核心解释变量和控制变量.

  • 核心解释变量: 我们最感兴趣的变量, 因此我们特别希望得到对其系数的 一致估计 (当样本容量无限增大时, 收敛于待估计参数的真值 ).
  • 控制变量: 我们可能对于这些变量本身并无太大兴趣; 而之所以把它们也 放入回归方程, 主要是为了 “控制住” 那些对被解释变量有影响的遗漏因素.

2.4. Multicollinearity

多重共线性

如果某个回归系数的 $t$ 检验不通过, 那么有两种常见的可能:

  • 这个系数对应的自变量对因变量的影响并不显著.
  • 自变量之间存在共线性. (值得是多元线性回归方程中, 自变量之间有较强的线性关系)

如何定量地判断是否存在多重共线性问题:

我们定义回归模型的方差膨胀因子 $VIF:=\displaystyle\max_{1\le i\le k}\left\{VIF_i\right\}$, 其中:

$$VIF_i:=\frac1{1-r_{1\sim k \backslash i}^2} $$

一个经验规则是: 如果 $VIF\ge 10$, 那么可以认为该回归方程有严重的多重共线性.

在这样的情况下, 我们应当设法重新建立更加简单的回归方程. 解决多重共线性的方法有如下两种:

  • Forward Selection (向前逐步回归): 将自变量逐个引入模型, 每引入一个自变量后都要进行检验, 显著时才加入回归模型. (缺点: 随着以后其他自变量的引入, 原来显著的自变量也可能又变为不显著了, 但是, 并没有将其及时从回归方程中剔除掉.)
  • Backward elimination (向后逐步回归): 与向前逐步回归相反, 先将所有变量均放入模型, 之后尝试将其中一个自变量从模型中剔除, 看整个模型解释因变量的 变异是否有显著变化, 之后将最没有解释力的那个自变量剔除; 此过程不断迭代, 直到没有自变量符合剔除的条件. (缺点: 一开始把全部变量都引入回归方程, 这样计算量比较大. 若对一些不重要的变量, 一开始就不引入, 这样就可以减少一些计算. 当然这个缺点随着现在计算机的能力的提升, 已经变得不算问题了）

但是实际上, 逐步回归法也并不完美:

  • 向前逐步回归和向后逐步回归的结果可能不同.
  • 不要轻易使用逐步回归分析, 因为剔除了自变量后很有可能会产生新的问题, 例如内生性问题.

有没有更加优秀的筛选方法？那就是每种情况都尝试一次, 最终一 共有 $\displaystyle\sum_{k=0}^n C_n^k=2^n-1$ 种可能. 如果自变量很多, 那么计算相当费时.

3. Non-linear Regressive Analysis

3.1. 基本步骤

进行变量变换实现线性化 $\to$ 进行线性回归预测 $\to$ 进行反变换实现数据还原

3.2. 非线性函数

双曲线模型: $\frac{1}{y}=a+\frac{b}{x}$

指数模型: $y=ae^{bx}$

对数模型: $y=a+b\ln x$

幂函数模型: $y=ax^b$

什么时候取对数?

伍德里奇的《计量经济学导论，现代观点》, 第六章176-177页有详细的论述:

取对数意味着原被解释变量对解释变量的弹性, 即百分比的变化而不是数值的变化; 目前, 对于什么时候取对数还没有固定的规则, 但是有一些经验法则

  • 与市场价值相关的, 例如价格, 销售额, 工资等都可以取对数;
  • 以年度量的变量, 如受教育年限, 工作经历等通常不取对数;
  • 比例变量, 如失业率, 参与率等, 两者均可;
  • 变量取值必须是非负数, 如果包含0, 则可以对 $y$ 取对数 $\ln (1+y)$;