2024-06-30

Neural Network

1. MLP

1.1. BP Neural Network

Back Propagation (反向传播, BP) 神经网络指的是应用了误差反向传播 (Error Back Propagation)算法的多层感知机. BP本质是学习算法, 被广泛应用到MLP, ADE, KBF, DNN中. 因此很多时候, 又把 MLP 称为 BP 神经网络. BP 神经网络在实现上重点关注如下的四个概念.

$$def.$$ Error

在经典的感知器中, 误差 $E:=\displaystyle \sum_{i=1}^NE_i=\sum_{i=1}^N(y_i-\hat y_i)$ .

对于多层感知机 (BP神经网络), 误差 $E:=\displaystyle \sum_{i=1}^N\frac 1 2(y_i-\hat y_i)^2$

这里的 $\displaystyle {1\over 2}$ 只是为了后续求导的便利, 本身没有特殊意图.

$$def.$$ Delta Rule

Delta Rule 刻画了人工神经网络的权重更新规则.

Delta Rule是基于误差平面的. 误差平面是神经网络所表示的函数在(训练)数据集上的累积误差. 每一个神经网络权值向量都对应误差平面中的一个点. 应用 Delta Rule 时, 激励函数必须是连续的和可微分的.

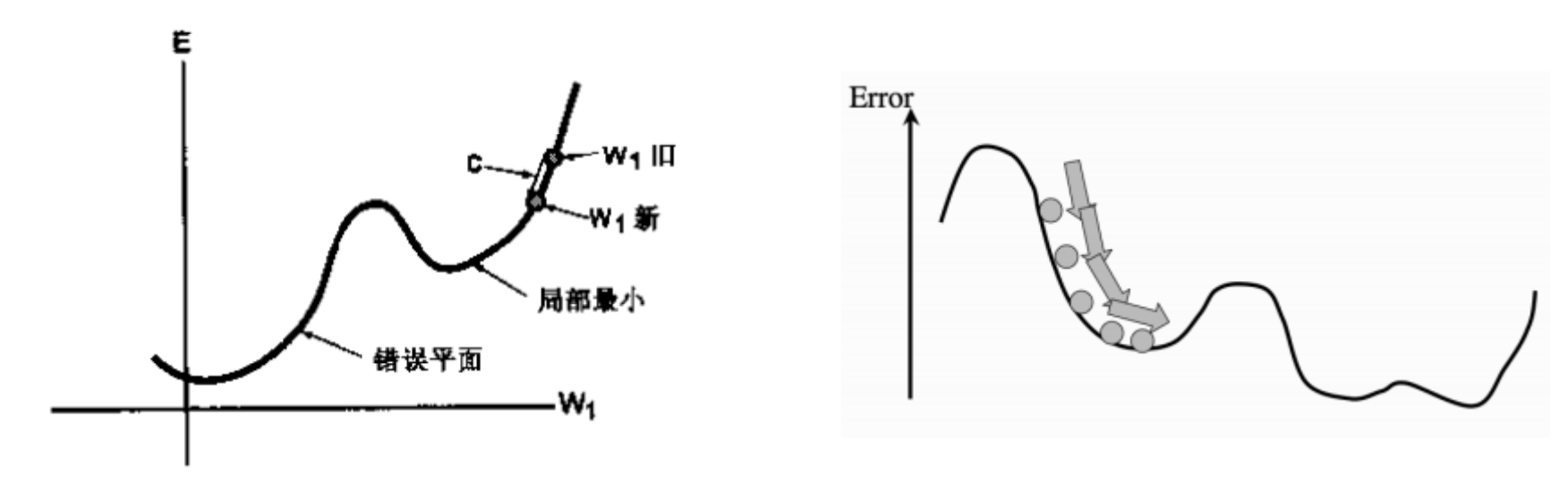
对于输入 $(\boldsymbol x,\boldsymbol y)$ , 假设神经网络的输出为 $\hat {\boldsymbol y}$ , 误差为 $$E$$ ,

\left\{ \begin{align} E&=\frac{1}{2} \sum_{i}\left(y_{i}-\hat y_{i}\right)^{2} \quad \text{subject to}\quad \boldsymbol {\hat y}(\boldsymbol x)=f(\boldsymbol w ^{\mathsf T}\cdot \boldsymbol x) \\ \Delta w_{k}&=-c \frac{\partial E}{\partial w_{k}}=-c \frac{\partial E}{\partial\hat y_{i}} \cdot \frac{\partial\hat y_{i}}{\partial w_{k}} \\ \frac{\partial \text {E}}{\partial \hat y_{i}}&=\frac{1}{2}\cdot \sum_{i}\frac{\partial\left(y_{i}-\hat y_{i}\right)^{2}}{\partial \hat y_i}=\frac{1}{2} \cdot \frac{\partial \left(y_{i}-\hat y_{i}\right)^{2}}{\partial\hat y_i} \end{align} \right.

因为输出层中的节点的误差并不影响其他节点, 因此:

\frac{1}{2} \cdot \frac{\partial \left(y_{i}-\hat y_{i}\right)^{2}}{\partial\hat y_i}=(\hat y_i-y_i)

同时根据偏导数的定义, 我们有:

\frac{\partial \hat{y}_{i}}{\partial w_{k}}=x_k\cdot f'(w_ix_i)

再代入到第二条等式中, 得到:

\begin {align} \Delta w_{k}&=c\cdot (y_i-\hat y_i)\cdot \frac{\partial \hat{y}_{i}}{\partial w_{k}}\\ &=c\cdot (y_i-\hat y_i)\cdot x_k\cdot f'(w_ix_i) \end {align}

其中, 学习常数 $$c$$ 对 Delta Rule 的性能有很重要的影响, $$c$$ 决定了在一步学习过程中权值变化的快慢, $$c$$ 越大, 权值朝最优值移动的速度越快. 然而, $$c$$ 过大会越过最优值或在最优值附近振荡. 尽管 Delta Rule 本身不能克服单层神经网络的局限, 但是它的一般形式是 BP 的核心.

$$def.$$ Activation Function

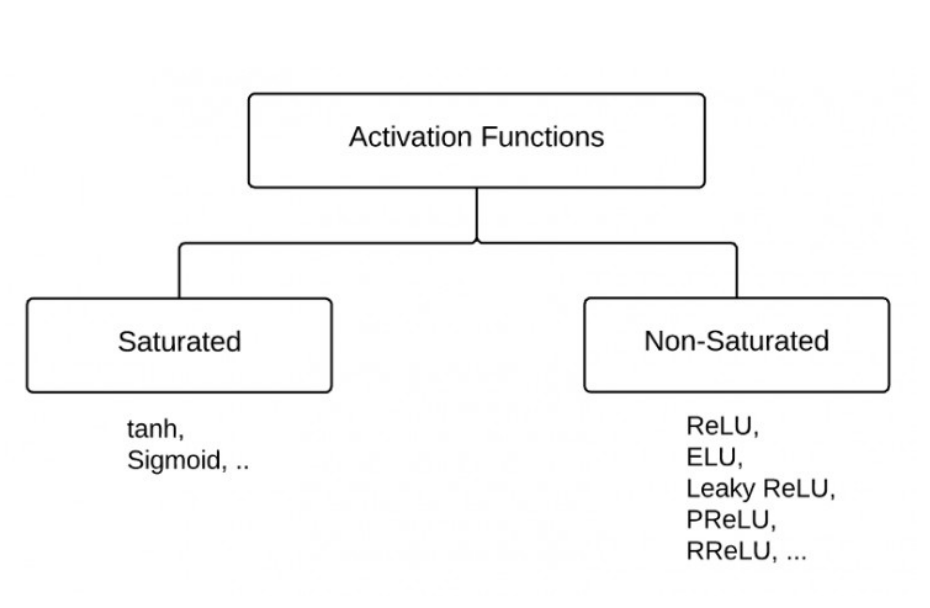
saturated activation function 指的是:

梯度消失
非以0为中心
指数计算代价大

$$def.$$ BP Learning Process

总的来说, BP的学习过程包括如下的两个方面

前向阶段: 网络突触的权值固定, 输入信号在网络中正向一层一层传播, 直到到达输出端, 获得网络的输出.
反向阶段: 通过比较网络的输出与期望输出, 产生一个误差信号. 误差信号通过网络反向一层一层传播, 在传播过程中对网络突触的权值进行修正.

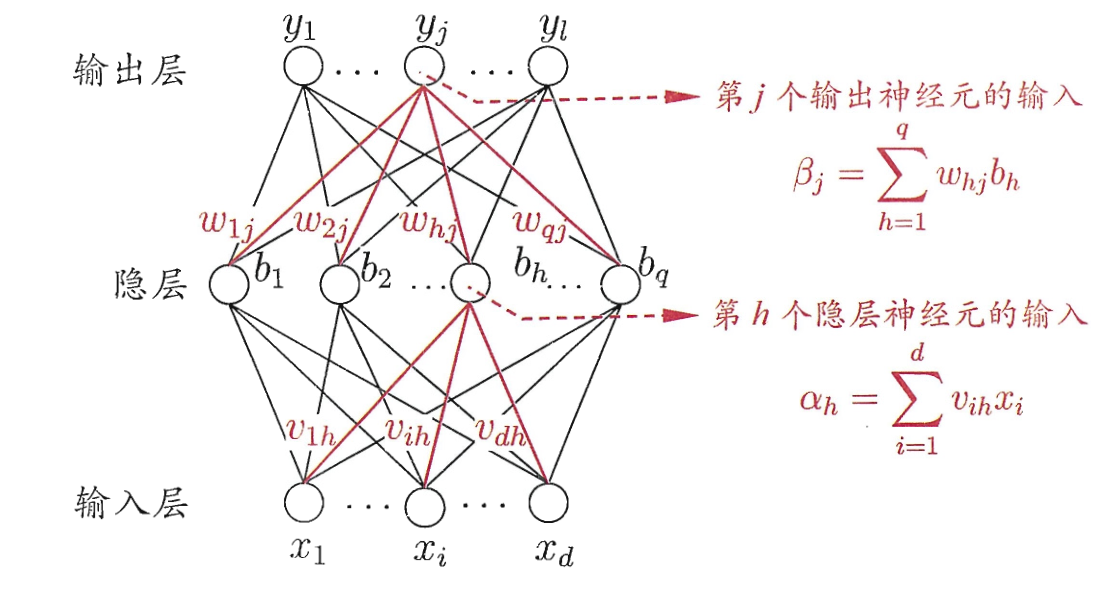
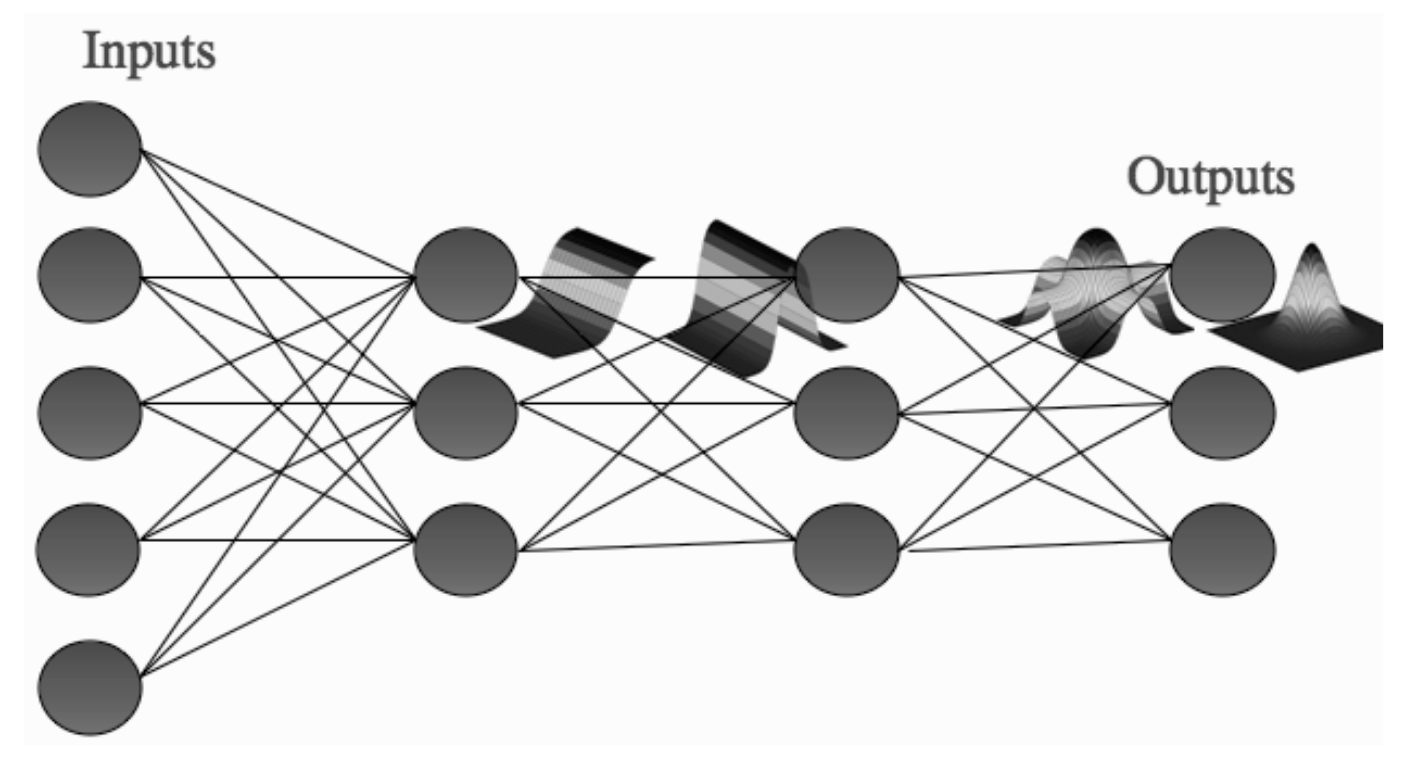
这里PPT上写的非常混乱, 于是直接看西瓜书了.

更加具体地说, 对于给定的训练集 $D=\left\{\left(\boldsymbol{x}_{1}, \boldsymbol{y}_{1}\right)\right. \left.\left(\boldsymbol{x}_{2}, \boldsymbol{y}_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, \boldsymbol{y}_{m}\right)\right\}, \boldsymbol{x}_{i} \in \mathbb{R}^{d}, \boldsymbol{y}_{i} \in \mathbb{R}^{l}$ , 也就是说有 $$m$$ 条数据, 每条数据刻画 $$d$$ 个属性和 $$l$$ 个输出. 如上图所示. 输出层第 $$j$$ 个神经元的阈值记作 $\theta_j$ , 隐层第 $$h$$ 个神经元的阈值记作 $\gamma_h$ , 输入层第 $$i$$ 个神经元与隐层第 $$h$$ 个神经元之间的连接权为 $v_{ih}$ , 隐层第 $$h$$ 个神经元与输出层第 $$j$$ 个神经元的连接权为 $w_{hj}$ . 对于训练集 $\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{k}\right)$ , 假设神经网络的输出为 $\hat{\boldsymbol{y}}_{k}=\left(\hat{y}_{1}^{k}, \hat{y}_{2}^{k}, \ldots, \hat{y}_{l}^{k}\right)$ , 也就是说

\hat{y}_{j}^{k}=f\left(\beta_{j}-\theta_{j}\right)

根据上述的 Delta Rule, 我们发现 BP 算法基于梯度下降的策略, 也就是说对于网络在 $\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{k}\right)$ 上的误差 $\displaystyle E_{k}=\frac{1}{2} \sum_{j=1}^{l}\left(\hat{y}_{j}^{k}-y_{j}^{k}\right)^{2}$ 以及给定的学习率 $\eta$ , 有

\Delta w_{h j}=-\eta \frac{\partial E_{k}}{\partial w_{h j}}

我们从意义的角度展开这样的偏导

\frac{\partial E_{k}}{\partial w_{h j}}=\frac{\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac{\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} \cdot \frac{\partial \beta_{j}}{\partial w_{h j}}

其中

\beta_{j}=\sum_{h=1}^{q} w_{h j} b_{h}\quad \frac{\partial \beta_{j}}{\partial w_{h j}}=b_{h}

并且 $$f$$ 作为 $\text{sigmoid}$ 函数具有这样trivial的性质

f^{\prime}(x)=f(x)(1-f(x))

代入到上式中, 我们有

\begin{aligned} \text{let}\quad g_j &=\frac{\partial E_{k}}{\partial w_{h j}} \\ &=-\frac{\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac{\partial \hat{y}_{j}^{k}}{\partial \beta_{j}}\cdot b_h \\ & =-\left(\hat{y}_{j}^{k}-y_{j}^{k}\right) f^{\prime}\left(\beta_{j}-\theta_{j}\right)b_h \\ & =\hat{y}_{j}^{k}\left(1-\hat{y}_{j}^{k}\right)\left(y_{j}^{k}-\hat{y}_{j}^{k}\right)b_h \\ \implies \Delta w_{h j} &=-\eta g_jb_h \end{aligned}

类似地也能推导出

\begin{aligned} \Delta \theta_{j} & =-\eta g_{j} \\ \Delta v_{i h} & =\eta e_{h} x_{i} \\ \Delta \gamma_{h} & =-\eta e_{h}\end{aligned}

其中:

\begin{aligned} e_{h} & =-\frac{\partial E_{k}}{\partial b_{h}} \cdot \frac{\partial b_{h}}{\partial \alpha_{h}} \\ & =-\sum_{j=1}^{l} \frac{\partial E_{k}}{\partial \beta_{j}} \cdot \frac{\partial \beta_{j}}{\partial b_{h}} f^{\prime}\left(\alpha_{h}-\gamma_{h}\right)\\ &=\sum_{j=1}^{l} w_{h j} g_{j} f^{\prime}\left(\alpha_{h}-\gamma_{h}\right) \\ &=b_{h}\left(1-b_{h}\right) \sum_{j=1}^{l} w_{h j} g_{j} . \end{aligned}

1.2. Other Details

这里介绍 BP 实际上使用时的细节问题, 大概算是一种工艺问题

1. Original weight

很自然地, 我们会想随机选择初始权重, 也就是说对于 $\boldsymbol w=(w_1,w_2,\ldots,w_n)^{\mathsf T}$ :

\boldsymbol w\sim\mathbb N(0,1)

但根据方差的基本性质 (独立变量和的方差 = 独立变量方差的和) 我们发现在这样的情况下:

\boldsymbol w^{\mathsf T}\boldsymbol x\sim\mathbb N(0,n)

进一步导致激活函数饱和, 梯度趋近于0, 学习失效. 因此我们选取 $\boldsymbol w$ 满足

\boldsymbol w\sim\mathbb N(0,\frac1{\sqrt n})

2. Activation Function

分类问题: $\text{sigmoid}$ 函数
回归问题: 一次函数
$\text{Soft-max}$ 激活函数: $\displaystyle y_{\kappa}=g\left(h_{\kappa}\right)=\frac{\exp \left(h_{\kappa}\right)}{\displaystyle \sum_{k=1}^{N} \exp \left(h_{\kappa}\right)}$
其他深度学习中用的非饱和激活函数

3. Training Order

批量训练(梯度下降 gradient descent): 计算所有训练样本的误差和. 缺点: 计算代价大/收敛速度快/局部极小 (local minimum).
顺序训练: 按次序计算每个训练样本的误差. 不需要计算总误差, 快/局部极小/噪声敏感.
小批量训练(随机梯度下降 stochastic gradient descent): Mini-Batch $\to$ SGD. 适用于大规模数据.

这里的局部极小是一种很常见的问题. 形式化地, 如果对于 $\boldsymbol w^*$ , $\theta^*$ :

\exists \epsilon>0:\forall(\boldsymbol{w} ; \theta) \in\left\{(\boldsymbol{w} ; \theta) \mid\left\|(\boldsymbol{w} ; \theta)-\left(\boldsymbol{w}^{*} ; \theta^{*}\right)\right\| \leqslant \epsilon\right\} \quad s.t.\quad E(\boldsymbol{w} ; \theta) \geqslant E\left(\boldsymbol{w}^{*} ; \theta^{*}\right)

那么称 $(\boldsymbol w^*;\theta^*)$ 为局部极小解. 这一部分在优化与搜索中有更为详细的阐述.

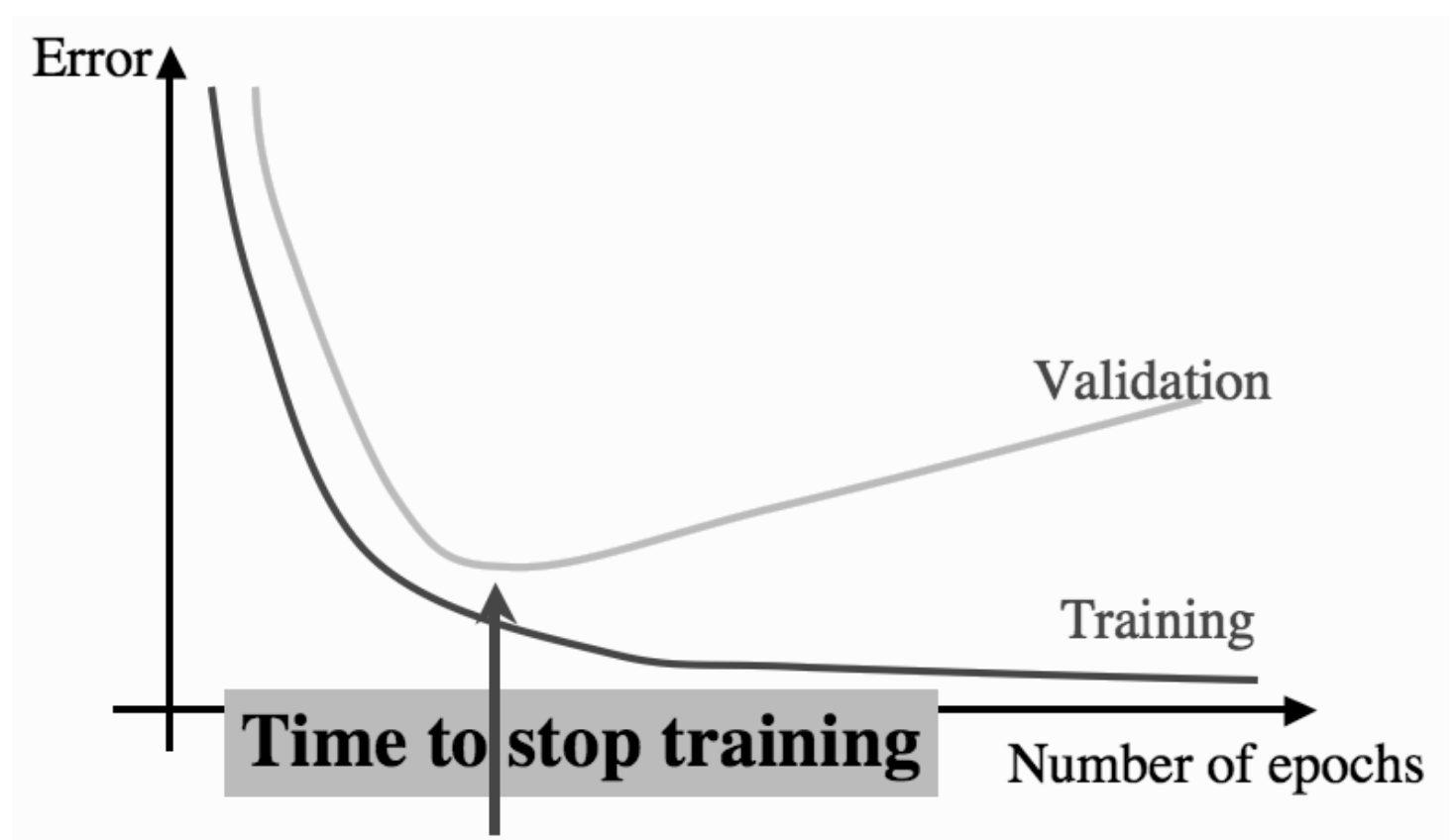
4. When to stop

防止过拟合.

设定固定迭代步数
设定误差小于某个固定阈值
以上两者的结合

2. Auto-Encoder

自动编码器是一种无监督的神经网络模型, 它可以学习到输入数据的隐含特征, 这称为编码(coding), 同时用学习到的新特征可以重构出原始输入数据, 称之为解码(decoding). 从直观上来看, 自动编码器可以用于特征降维, 类似主成分分析PCA, 但是其相比PCA其性能更强, 这是由于神经网络模型可以提取更有效的新特征. 除了进行特征降维, 自动编码器学习到的新特征可以送入有监督学习模型中, 所以自动编码器可以起到特征提取器的作用.

自编码器由编码器和解码器组成，二者可以被分别定义为变换 $\phi$ 和 $\psi$ 使得：

\begin{array}{l}\phi: \mathcal{X} \rightarrow \mathcal{F} \\ \psi: \mathcal{F} \rightarrow \mathcal{X} \\ \phi, \psi=\underset{\phi, \psi}{\arg \min }\|\boldsymbol x-(\psi \circ \phi) \boldsymbol x\|^{2}\end{array}

在最简单的情况下，给定一个隐藏层，自编码器的编码阶段接受输入 $\boldsymbol x\in \mathbb R^d =\mathcal X$ 并将其映射到 ${\boldsymbol z \in \mathbb {R} ^{p}={\mathcal {F}}}$

\boldsymbol{z}=\sigma(\boldsymbol{w} \boldsymbol{x}+\boldsymbol{b})

自编码器的解码阶段映射 $\boldsymbol z$ 到重构 $\boldsymbol x'$

\boldsymbol{x}^{\prime}=\sigma^{\prime}\left(\boldsymbol w^{\prime} \boldsymbol{z}+\boldsymbol{b}^{\prime}\right)

自编码器被训练来最小化重建误差 (如平方误差):

\mathcal{L}\left(\boldsymbol{x}, \boldsymbol{x}^{\prime}\right)=\left\|\boldsymbol{x}-\boldsymbol{x}^{\prime}\right\|^{2}=\left\|\boldsymbol{x}-\sigma^{\prime}\left(\boldsymbol{w}^{\prime}(\sigma(\boldsymbol{w} \boldsymbol{x}+\boldsymbol{b}))+\boldsymbol{b}^{\prime}\right)\right\|^{2}

3. Other Neural Networks

3.1. RBF

RBF (Radial Basis Function, 径向基函数) 网络 (Broomhead and Lowe,1988) 是一种单隐层前馈神经网络, 它使用径向基函数作为隐层神经元激活函数, 而输出层则是对隐层神经元输出的线性组合．假定输入为 $$d$$ 维向量 $\boldsymbol x$ , 输出为实值, 则 RBF 网络可表示为:

\varphi(\boldsymbol{x})=\sum_{i=1}^{q} w_{i} \rho\left(\boldsymbol{x}, \boldsymbol{c}_{i}\right)

其中 $$q$$ 为隐层神经元个数, $\boldsymbol c_i$ 和 $$w_i$$ 分别是第 $$i$$ 个隐层神经元所对应的中心和权重, $\rho (\boldsymbol x, c_i)$ 是径向基函数, 这是某种沿径向对称的标量函数, 通常定义为样本 $\boldsymbol x$ 到数据中心 $\boldsymbol x_i$ 之间欧氏距离的单调函数. 常用的高斯径向基函数形如

\rho\left(\boldsymbol{x}, \boldsymbol{c}_{i}\right)=e^{-\beta_{i}\left\|\boldsymbol{x}-\boldsymbol{c}_{i}\right\|^{2}}

[Park and Sandberg, 1991] 证明，具有充分多隐层神经元的 RBF 网络能以任意精度逼近任意连续函数. 通常采用两步过程来训练RBF 网络:

第一步, 确定神经元中心 $\boldsymbol c_i$ , 常用的方式包括随机采样、聚类等
第二步, 利用 BP 算法等来确定参数 $$w_i$$ 和 $\beta_i$ .

我们发现形式上 RBF 与 Kernel SVM非常类似. 但实际上L

SVM中的高斯核函数可以看作与每一个输入点的距离, 不太适应于大样本和大的特征数的情况
RBF 神经网络对输入点做了一个聚类. RBF神经网络用高斯核函数时, 其数据中心 $\boldsymbol c_i$ 可以是训练样本中的抽样, 此时与 SVM 的高斯核函数是完全等价的.

3.2. ART

to-be-continued…

Welcome to My Blog 👉👈

@wuc9521