MATH►Mathematical Logic

2. First Order Logic

$$\newcommand{\vd}{\vdash} \newcommand{\vD}{\vDash} \newcommand{\gA}{𝔄} \newcommand{\gB}{𝔅} \newcommand{\gC}{ℭ} \newcommand{\gD}{𝔇} \newcommand{\gR}{𝕽} \newcommand{\gN}{𝕹} \newcommand{\mS}{\mathcal S} \newcommand{\mE}{\mathcal E} \newcommand{\te}{\models=\!\mid} \Huge\textbf{First Order Logic} $$

0. Preliminary Remarks

1. First-order Languages

def: $\textbf{SYMBOL}$

We assume that we have been given infinitely many distinct objects (which we call symbols), arranged as follows:

A. Logic Symbols

  1. Parenthesis: $\left(\right.$, $\left.\right)$.
  2. Sentential Connective Symbols: $\to$, $\neg$.
  3. Variables (one for each postive integer $n$):
$$\boldsymbol{v}_1, \boldsymbol{v}_2, \ldots $$
  1. Equality Symbol (optional): $=$.

B. Parameters

  1. Quantifier Symbol (量词): $\forall$.
  2. Predicable Symbol (谓词): For each positive integer $n$, some set (possibly empty) of symbols, called $n$-place predicate symbols.
  3. Constant Symbols (常量): Some set (possibly empty) of symbols.
  4. Function Symbols: For each positive integer $n$, some set (possibly empty) of symbols, called $n$-place function symbols.

Note that:

  • $\exists$: $\exists$ is not necessary because $\exists x$ can be replaced by $\neg\forall x\neg$
  • $=$: In A.3 we allow for the possibility of the equality symbol’s being present, but we do not assume its presence. Some languages will have it and others will not.
  • Constant Symbol: In B.2, the constant symbols are also called 0-place function symbols. (This allows a uniform treatment of constants and functions.)

To distinguish a first-order language from other (first-order) languages, we should at least:

  1. say whether or not the equality symbol is present, and
  2. say what the parameters are.

1.1. Formulas

$def: \textbf{Expression}$

An expression is any finite sequence of symbols. Of course most expressions are nonsensical, but there are certain interesting expressions: the terms and the wffs.

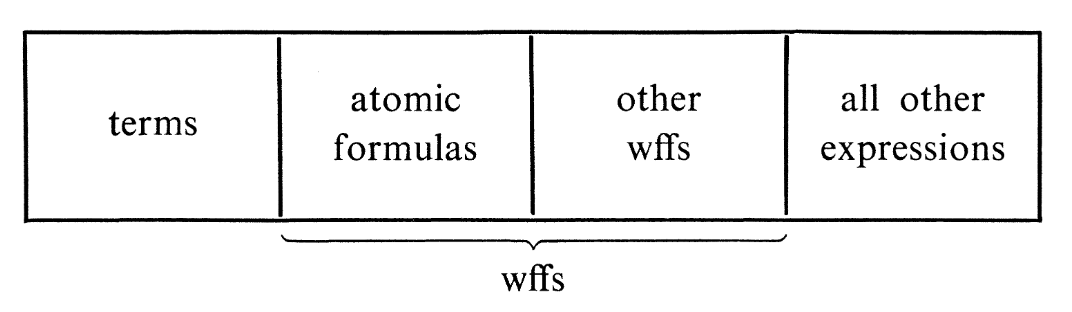
$def: \textbf{Term}$

The set of terms is the set of expressions that can be built up from the constant symbols and variables by applying (zero or more times) the $\mathcal F_f$ operations, where $\mathcal F_{f}$ is a $n$-place term-building operation defined from $f$, an $n$-place function symbol.

$$\mathcal F_{f}(\boldsymbol{v}_1, \boldsymbol{v}_2, \ldots, \boldsymbol{v}_n)=f(\boldsymbol{v}_1, \boldsymbol{v}_2, \ldots, \boldsymbol{v}_n)=f\boldsymbol{v}_1 \boldsymbol{v}_2 \ldots\boldsymbol{v}_n $$

If there are no function symbols (apart from the constant symbols), then the terms are just the constant symbols and the variables.

$def: \textbf{Atomic Formula}$

The set of atomic formulas is the set of expressions that can be built up from the predicate symbols and terms by applying (zero or more times) the $\mathcal F_P$ operations, where $\mathcal F_{P}$ is a $n$-place atomic formula-building operation defined from $P$, an $n$-place predicate symbol.

$$\mathcal F_{P}({t}_1, {t}_2, \ldots, {t}_n)=P({t}_1, {t}_2, \ldots, {t}_n)=P{t}_1 {t}_2 \ldots{t}_n $$

The atomic formulas will play a role roughly analogous to that played by the sentence symbols in sentential logic.

$def: \textbf{Well-formed Formula}$
The set of well-formed formulas (wffs) is the smallest set of expressions that contains all the atomic formulas and is closed under the following operations:

$$\begin{aligned} \text{1.}&\text{ If $\varphi$ is a wff, then $\neg\varphi$ is a wff.}\\ \text{2.}&\text{ If $\varphi$ and $\psi$ are wffs, then $(\varphi\to\psi)$ is a wff.}\\ \text{3.}&\text{ If $\varphi$ is a wff and $x$ is a variable, then $\forall x\varphi$ is a wff.} \end{aligned} $$

1.2. Free and Bound Variables

$def: \textbf{Occur Free}$

Consider any variable $x$. We define, for each wff $\alpha$, what it means for $x$ to occur free in $\alpha$. This we do by recursion:

  1. If $\alpha$ is atomic, then $x$ occurs free in $\alpha$ iff $x$ occurs in $\alpha$ as a symbol.
  2. $x$ occurs free in $\neg \alpha$ iff $x$ occurs free in $\alpha$.
  3. $x$ occurs free in $(\alpha\to\beta)$ iff $x$ occurs free in $\alpha$ or $x$ occurs free in $\beta$.
  4. $x$ occurs free in $\forall y\alpha$ iff $x$ occurs free in $\alpha$ and $x\neq y$.

$def: \textbf{Sentence}$

A wff $\alpha$ is a sentence iff no variable occurs free in $\alpha$.

Note that a sentence is the most meaningful wff.

Similar usages of variables occur elsewhere in mathematics. In

$$\sum_{i=1}^{100}a_{ij} $$

$i$ is a dummy variable (假变量) and $j$ is a free variable.

1.3. On Notation

We adopt then the following abbreviations and conventions. Here $\alpha$ and $\beta$ are formulas, $x$ is a variable, and $u$ and $t$ are terms.

  1. $(\alpha \lor \beta)$ abbreviates $((\neg \alpha) \to \beta)$.
  2. $(\alpha \land \beta)$ abbreviates $(\neg(\alpha \to (\neg \beta)))$.
  3. $(\alpha \leftrightarrow \beta)$ abbreviates $((\alpha \to \beta) \land (\beta \to \alpha))$.
  4. $\exists x\alpha$ abbreviates $\neg\forall x\neg\alpha$.
  5. $u=t$ abbreviates $=ut$.
  6. $u\neq t$ abbreviates $\neg = u t$.
  7. etc.

Note well that we are not changing our definition of what a wff is. We are simply conspiring to fix certain ways of naming wffs for convenience.

2. Truth and Models

In sentential logic we had truth assignments to tell us which sentence symbols were to be interpreted as being true and which as false.

In firstorder logic the analogous role is played by structures, which can be thought of as providing the dictionary for translations from the formal language into natural language.

With a structure $\gA$ we can know:

  • What collection of things the universal quantifier symbol ($\forall$) refers to, and

  • What the other parameters (the predicate and function symbols) denote.

$def:\textbf{Structure}$

Formally, a structure $\gA$ for a given first-order language is a function, whose domain is the set of all the symbols of the language, such that:

  1. $\gA$ assigns $\forall$ a nonempty set $\gA(\forall)$, or $|\gA|$, called the universe or domain of $\gA$.

  2. $\gA$ assigns to each $n$-place predicate symbol $P$ an $n$-ary relation $\gA(P)$ or $P^{\gA}\subseteq |\gA|^n$, a subset of $|\gA|^n$ for some $n$.

  3. $\gA$ assigns to each constant $c$ a member $\gA(c)$ or $c^{\gA}\in|\gA|$.

  4. $\gA$ assigns to each $n$-place function symbol $f$ an $n$-ary function $\gA(f)$ or $f^{\gA}:|\gA|^n\to|\gA|$.

注意这里所有的符号都是新定义的, 不要认为$|\gA|$是模长.

We would show that a sentence is sometimes true and sometimes false difference structures. For example, the sentence

$$\varphi: \exists x\forall y\neg yPx $$

where $P$ is a 2-place predicate symbol.

Consider Set Theory, we can define a structure $\gA$ as follows:

$$\begin{aligned} \gA(\forall)&=|\gA|=\mathbb N\\ \gA(P)&= \{(m, n)\mid m > n, m\in \mathbb N, n\in\mathbb N\} \end{aligned} $$

Except for $\forall$, $\in$ is the only predicate symbol in Set Theory.

So $\varphi$ can be translated to natural language as:

$$\text{There is a natural number $x$ such that}\\ \text{for every natural number $y$, $y$ is not larger than $x$.} $$

This is false obviously.

Or we can define another finite structure $\gB$ as follows:

$$\begin{aligned} \gB(\forall)&=|\gB|=\{a, b, c, d\}\\ \gB(P)&= \{(a, b), (b, a), (b, c), (c, c)\} \end{aligned} $$

where $P(x, y)$ means there is a directed edge from $x$ to $y$. So the graph of $\gB$ is:

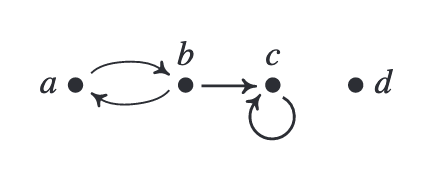
Then $\varphi$ can be translated to natural language as:

$$\text{There is a vertex such that}\\ \text{for any vertex, no edge points from the latter to the former.} $$

This is true because $d$ is such a vertex.

So before we define the “$\sigma$ is true in $\gA$”, denoted as

$$\vD_{\gA}\sigma $$

for sentences $\sigma$ and structures $\gA$,

we find it desirable first to define a more general concept involving wffs. Let:

$$\begin{aligned} \varphi&=\text{a wff of our language}\\ \gA&=\text{a structure for the language}\\ s&:V\to |\gA| \text{ (V is the set of all variables)} \end{aligned} $$

Then we will define what it means for $\gA$ to satisfy $\varphi$ with $s$, denoted by

$$\vD_{\gA}\varphi[s] $$

$def: \textbf{Satisfy}$

The formal definition of satisfaction proceeds as follows.

  1. for terms
    We define the extension
$$\bar s:T\to\gA $$

a function from the set $T$ of all terms into the universe of $\gA$. The idea is that $s(t)$ should be the member of the universe $|\gA|$ that is named by the term $t$. $\bar s$ is defined by recursion as follows:

  • for each variable $x$, $\bar s(x)=s(x)$
  • for each constant symbol $c$, $\bar s(c)=c^{\gA}$
  • if $t_i(i=1,2,\ldots,n)$ are terms and $f$ is a $n$-place function symbol, then
$$\bar s(ft_1\cdots t_n)=f^{\gA}(\bar s(t_1),\ldots,\bar s(t_n)) $$

3. A Parsing Algorithm

4. Deductive Calculus

5. Soundness and Completeness Theorems

In this section we establish two major theorems: the soundness of our deductive calculus

$$\Gamma \vd \phi \Rightarrow \Gamma \vD \phi $$

and its completeness

$$\Gamma \vD \phi \Rightarrow \Gamma \vd \phi $$. # 6. Models and Theories > This part is directly from [section 2](#truth-and-models) ## 6.1. Finite Models Some sentences have only infinite models, say, the negation of the sentence $$

\text{< is an ordering with no largest element.}

$$is true in every finite structure, which is **finitely valid**. Some sentences have only finite models, say, the sentence $$

111
$$

7. Interpretations between Theories

8. Non-standard Analysis